Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Funções 3.9 Funções exponenciais Referências

3.10 Funções logarítmicas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

A função logarítmica

f(x)=\log_{a}x,

(3.168)

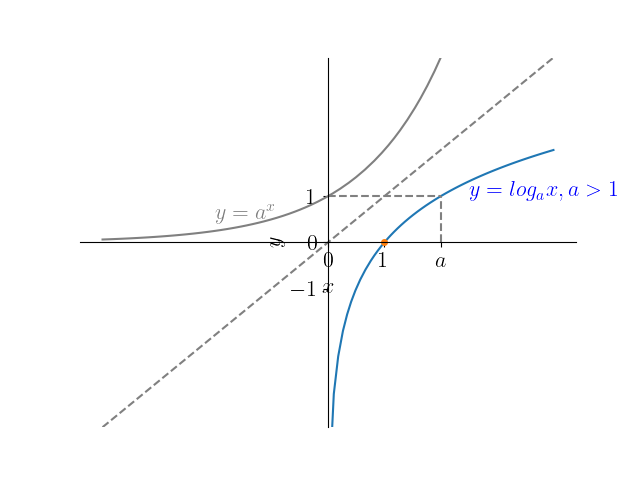
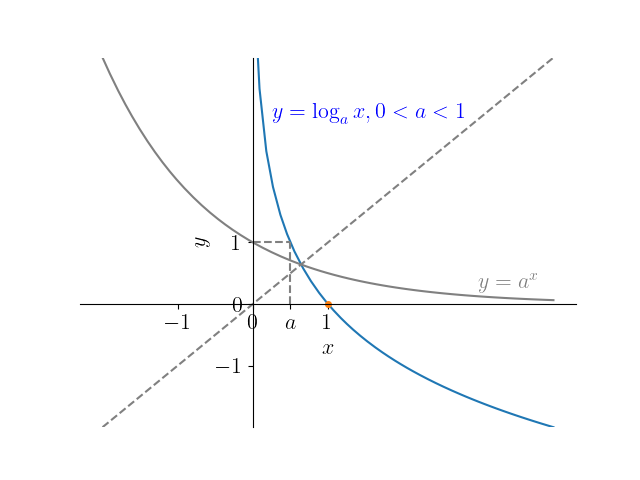
$a>0$ e $a\neq 1$ , é a função inversa da função exponencial $y=a^{x}$ . Consulte a Figura 3.44. O domínio da função logarítmica é $(0,\infty)$ e a imagem $(-\infty,\infty)$ .

Refer to caption — Figura 3.44: Esboços dos gráficos de funções logarítmicas: (acima) $y=\log_{a}x$ , $a>1$ ; (abaixo) $y=\log_{a}x$ , $0<a<1$ .

Observação 3.10.1.

Quando a base é o número de Euler $e\approx 2,718281828459045$ , chamamos $y=\log_{e}x$ de função logarítmica natural e denotamo-la por $y=\ln x$ .

No SymPy, podemos computar $\log_{a}x$ com a função log(x,a). O $\ln x$ é computado com log(x).

Vamos estudar algumas propriedades dos logaritmos:

a)

$\displaystyle\boldsymbol{\log_{a}x=y\Leftrightarrow a^{y}=x}$ ;

Isto é por si a definição da função logarítmica, da qual temos que ela é a função inversa da função exponencial.
b)

$\displaystyle\boldsymbol{\log_{a}1=0}$ ;

Da propriedade a), temos $\log_{a}1=y$ para

$\displaystyle a^{y}=1$ (3.169)

$\displaystyle a^{y}=a^{0}$ (3.170)

$\displaystyle y=0$ (3.171)
c)

$\displaystyle\boldsymbol{\log_{a}a=1}$ ;

Da propriedade a), temos $\log_{a}a=y$ para

$\displaystyle a^{y}=a$ (3.172)

$\displaystyle a^{y}=a^{1}$ (3.173)

$\displaystyle y=1$ (3.174)
d)

$\displaystyle\boldsymbol{\log_{a}a^{x}=x}$ ;

Segue imediatamente do fato de que a função logarítmica $y=\log_{a}x$ é a função inversa da função exponencial $y=a^{x}$ .
e)

$\displaystyle\boldsymbol{a^{\log_{a}x}=x}$ ;

Segue imediatamente do fato de que a função exponencial $y=a^{x}$ é a função inversa da função logarítmica $y=\log_{a}x$ .
f)

$\displaystyle\boldsymbol{\log_{a}x\cdot y=\log_{a}x+\log_{a}y}$ ;

Sejam $z=\log_{a}x\cdot y$ , $z_{x}=\log_{a}x$ e $z_{y}=\log_{a}y$ . Logo, temos

$\displaystyle a^{z}=x\cdot y$ (3.175)

$\displaystyle a^{z}=a^{z_{x}}\cdot a^{z_{y}}$ (3.176)

$\displaystyle a^{z}=a^{z_{x}+z_{y}}$ (3.177)

$\displaystyle z=z_{x}+z_{y}$ (3.178)
g)

$\displaystyle\boldsymbol{\log_{a}\frac{x}{y}=\log_{a}x-\log_{a}y}$ ;

Sejam $z=\log_{a}\frac{x}{y}$ , $z_{x}=\log_{a}x$ e $z_{y}=\log_{a}y$ . Logo, temos

$\displaystyle a^{z}=x\cdot y$ (3.179)

$\displaystyle a^{z}=a^{z_{x}}\cdot a^{z_{y}}$ (3.180)

$\displaystyle a^{z}=a^{z_{x}+z_{y}}$ (3.181)

$\displaystyle z=z_{x}+z_{y}$ (3.182)
h)

$\displaystyle\boldsymbol{\log_{a}x^{r}=r\cdot\log_{a}x}$ .

Seja $z=\log_{a}x$ . Temos

$\displaystyle a^{z}=x$ (3.183)

$\displaystyle\left(a^{z}\right)^{r}=x^{r}$ (3.184)

$\displaystyle a^{r\cdot z}=x^{r}$ (3.185)

$\displaystyle r\cdot\log x=\log_{a}x^{r}$ (3.186)
i)

$\displaystyle\boldsymbol{\log_{a}x=\frac{\log_{b}x}{\log_{b}a}}$

Sejam $z=\log_{a}x$ , $z_{x}=\log_{b}x$ e $z_{a}=\log_{b}a$ . Temos

$\displaystyle b^{z_{a}}=a$ (3.187)

$\displaystyle(b^{z_{a}})^{z}=a^{z}$ (3.188)

$\displaystyle b^{z_{a}\cdot z}=x$ (3.189)

$\displaystyle b^{z_{a}\cdot z}=b^{z_{x}}$ (3.190)

$\displaystyle z_{a}\cdot z=z_{x}$ (3.191)

$\displaystyle z=\frac{z_{x}}{z_{a}}$ (3.192)

Exemplo 3.10.1.

Estudemos os seguintes casos:

a)

$\log_{2}2=1$ (3.193)
b)

$\displaystyle\log_{2}8$ $\displaystyle=\log_{2}2^{3}$ (3.194)

$\displaystyle=3\cdot\log_{2}2$ (3.195)

$\displaystyle=3$ (3.196)
c)

$\ln e^{-x}=-x$ (3.197)
d)

$e^{\ln x^{2}}=x^{2}$ (3.198)

Exercícios resolvidos

ER 3.10.1.

Faça o esboço do gráfico de $f(x)=\ln(x+2)+1$ e determine seu domínio.

Solução.

Para fazermos o esboço do gráfico de $f(x)=\ln(x+2)+1$ , podemos começar com o gráfico de $f_{1}(x)=\ln x$ . Então, podemos transladá-lo 2 unidades à esquerda, de forma a obtermos $f_{2}(x)=\ln(x+2)=f_{1}(x+2)$ . Por fim, transladamos o gráfico de $f_{2}(x)$ uma unidade para cima, obtendo o esboço do gráfico de $f(x)=\ln(x+2)+1=f_{2}(x)+1$ . Veja a Figura 3.45.

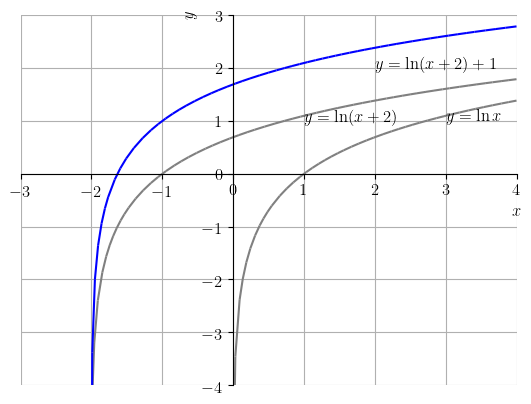
Ainda, o domínio de $\ln x$ é $(0,\infty)$ . Como, $f(x)=\ln(x+2)+1$ é uma translação de duas unidades à esquerda e uma para cima de $\ln x$ , temos que o domínio de $f(x)$ é $(-2,\infty)$ .

ER 3.10.2.

Resolva a seguinte equação para $x$

\ln(x+2)-1=1.

(3.199)

Solução.

Podemos calcular a solução pelos seguintes passos:

	$\displaystyle\ln(x+2)+1=1$		(3.200)
	$\displaystyle\ln(x+2)=0$		(3.201)
	$\displaystyle e^{\ln(x+2)}=e^{0}$		(3.202)
	$\displaystyle x+2=e^{0}$		(3.203)
	$\displaystyle x=1-2=-1.$		(3.204)

Com o SymPy, podemos computar a solução com os seguintes comandos:

⬇

1 from sympy import *

2 solve(Eq(log(x+2)+1,1),x)

Exercícios

E. 3.10.1.

Calcule o valor de:

a)

$2\ln 2-\ln 3+\ln\frac{3}{4}$
b)

$\log_{10}50-\log_{10}5$

Resposta.

a) $0$ ; b) $1$

E. 3.10.2.

Faça o esboço do gráfico de $f(x)=\log(x-2)-1$ e determine seu domínio.

Resposta.

Dica: use um pacote computacional de matemática simbólica para verificar o esboço de seu gráfico. Domínio: $(2,\infty)$ .

E. 3.10.3.

Resolva para $x$ :

a)

$\ln x^{2}=4$
b)

$\log_{\sqrt{2}}(x+1)=0$

Resposta.

a) $x=e^{2}$ ; b) $x=0$

E. 3.10.4.

Mostre que

\ln|y|-\ln\left|1-\frac{y}{K}\right|=rt+c

(3.206)

tem como solução a função logística

y=\frac{K}{1+\frac{K}{c}e^{-rt}}

(3.207)

E. 3.10.5.

(Aplicação.) O fenômeno de desintegração espontânea do núcleo de um átomo com a emissão de algumas radiações é chamado de radioatividade³⁸³⁸endnote: ³⁸Fonte: Wikipédia.. A lei fundamental do decaimento radiativo estabelece que a taxa de decaimento é proporcional ao número de átomos que ainda não decaíram. Isto nos fornece a equação da lei básica da radioatividade

N=N_{0}e^{-\lambda t}

(3.208)

onde, $N=N(t)$ é o número de átomos no tempo $t$ , $N_{0}\geq 0$ é o número de átomos presentes no tempo inicial $t=0$ e $\lambda>0$ é a constante de decaimento.

A meia-vida do plutônio ( ${}^{236}\text{Pu}$ ) é de aproximadamente $2,86$ anos. Determine a sua constante de decaimento $\lambda$ .

Resposta.

$\displaystyle\lambda=\frac{1}{2,86}\ln 2$

Notas

1 Giuseppe Peano, 1858 - 1932, matemático italiano. Fonte: Giuseppe Peano
2 Axioma do Princípio da Indução.
3 Também, chamado de módulo ou norma.
4 Introduziremos os números reais na sequência.
5 Mais precisamente, as operações são realizadas em ponto flutuante. Para mais informações, consulte aritmética de máquina.
6 Estas propriedades são válidas desde que as operações estejam bem definidas. Por exemplo, a segunda propriedade elencada somente é válida no caso de $a\neq 0$ .
7 Um número $m\in\mathbb{N}^{*}$ é divisor de $n\in\mathbb{Z}$ , quando $m/n\in\mathbb{Z}$ .
8 Sobre razão irredutível, consulte a Observação 1.2.10.
9 Número múltiplo inteiro de $2$ .
10 O quadrado de um número ímpar é um número ímpar. Número ímpar é um número inteiro não divisível por $2$ .
11 Do inglês, not a number.
12 Dica: consulte o método sympy.factorint.
13 $|x|=x$ , $x\geq 0$ e $|x|=-x$ , caso contrário.
14 Somente no caso de $E_{3}\in\mathbb{R}^{*}$
15 Identidade é o nome dado a uma equação que é satisfeita para todos os possíveis valores de sua(s) incógnita(s).
16 $\sqrt{x^{2}}=|x|$ .
17 Bhaskara Akaria, 1114 - 1185, matemático indiano. Fonte: Wikipédia.
18 Quando bem definido.
19 Lembremos a tricotomia dos números reais. Consulte a Subseção 1.3.3.
20 Notemos que a desigualdade se inverte ao multiplicarmos a inequação por um número negativo.
21 O valor de saída $f(x)$ pertence ao conjunto $Y$ .
22 Esta função também pode ser definida por $|x|=\sqrt{x^{2}}$ .
23 números reais.
24 Mais corretamente, coeficiente do termo constante.
25 eixo das abscissas
26 Uma função é dita ser definida em toda parte quando seu domínio é $(\infty,\infty)$
27 Em geral utilizaremos a medida em radianos para ângulos.
28 Circunferência do círculo de raio 1.
29 Por definição, $f(x)$ é função ímpar quando $f(x)=-f(-x)$ .
30 Por definição, $f(x)$ é uma função par quando $f(x)=f(-x)$ .
31 Observemos que não podemos simplificar o $x$ , pois a função $y=x$ é diferente da função $y=x^{2}/x$ .
32 Atenção! Não confundamos com a função $(f(x))^{-1}=1/f(x)$ .
33 Leonhard Paul Euler, 1707 - 1783, matemático e físico suíço. Fonte: Wikipédia.
34 Veja a Observação
35 Svante August Arrhenius, 1859-1927, químico sueco. Fonte: Wikipédia.
36 Modelos matemáticos baseados em neurônios biológicos.
37 Fonte: Wikipédia.
38 Fonte: Wikipédia.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |

	$\displaystyle a^{y}=1$		(3.169)
	$\displaystyle a^{y}=a^{0}$		(3.170)
	$\displaystyle y=0$		(3.171)

	$\displaystyle a^{y}=a$		(3.172)
	$\displaystyle a^{y}=a^{1}$		(3.173)
	$\displaystyle y=1$		(3.174)

	$\displaystyle a^{z}=x\cdot y$		(3.175)
	$\displaystyle a^{z}=a^{z_{x}}\cdot a^{z_{y}}$		(3.176)
	$\displaystyle a^{z}=a^{z_{x}+z_{y}}$		(3.177)
	$\displaystyle z=z_{x}+z_{y}$		(3.178)

	$\displaystyle a^{z}=x\cdot y$		(3.179)
	$\displaystyle a^{z}=a^{z_{x}}\cdot a^{z_{y}}$		(3.180)
	$\displaystyle a^{z}=a^{z_{x}+z_{y}}$		(3.181)
	$\displaystyle z=z_{x}+z_{y}$		(3.182)

	$\displaystyle a^{z}=x$		(3.183)
	$\displaystyle\left(a^{z}\right)^{r}=x^{r}$		(3.184)
	$\displaystyle a^{r\cdot z}=x^{r}$		(3.185)
	$\displaystyle r\cdot\log x=\log_{a}x^{r}$		(3.186)

	$\displaystyle b^{z_{a}}=a$		(3.187)
	$\displaystyle(b^{z_{a}})^{z}=a^{z}$		(3.188)
	$\displaystyle b^{z_{a}\cdot z}=x$		(3.189)
	$\displaystyle b^{z_{a}\cdot z}=b^{z_{x}}$		(3.190)
	$\displaystyle z_{a}\cdot z=z_{x}$		(3.191)
	$\displaystyle z=\frac{z_{x}}{z_{a}}$		(3.192)

$\displaystyle\log_{2}8$	$\displaystyle=\log_{2}2^{3}$	(3.194)
	$\displaystyle=3\cdot\log_{2}2$	(3.195)
	$\displaystyle=3$	(3.196)