| | | | |

3.8 Propriedades de Funções

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.8.1 Funções Crescentes ou Decrescentes

Uma da função f é dita ser crescente quando f⁢(x1)<f⁢(x2) para todos x1<x2 no seu domínio. É dita não decrescente quando f⁢(x1)≤f⁢(x2) para todos os x1<x2 no seu domínio. Analogamente, é dita decrescente quando f⁢(x1)>f⁢(x2) para todos x1<x2. E, por fim, é dita não crescente quando f⁢(x1)≥f⁢(x2) para todos x1<x2, sempre no seu domínio. Em todos estes casos, diz que f é uma função monótona.

Exemplo 3.8.1.

Estudemos os seguintes casos:

  1. a)

    A função identidade f⁢(x)=x é crescente.

  2. b)

    A função valor absoluto y=|x| não é monótona.

  3. c)

    A função h⁢(x)=−x3 é uma função decrescente.

  4. d)

    A seguinte função definida por partes

    f⁢(x)={x+1,x≤0,2,0<x≤1,(x−1)2+2,x>1 (3.144)

    é não decrescente.

Também, definem-se os conceitos análogos de uma função ser crescente ou decrescente em um dado intervalo.

Exemplo 3.8.2.

A função f⁢(x)=x2 é uma função decrescente no intervalo (−∞⁢,0] e crescente no intervalo [0,∞).

3.8.2 Funções Pares ou Ímpares

Uma dada função f é dita par quando f⁢(x)=f⁢(−x) para todo x no seu domínio. Ainda, é dita ímpar quando f⁢(x)=−f⁢(−x) para todo x no seu domínio.

Exemplo 3.8.3.

Vejamos os seguintes casos:

  • •

    f⁢(x)=x2 é uma função par.

  • •

    f⁢(x)=x3 é uma função ímpar.

  • •

    f⁢(x)=sen⁡x é uma função ímpar.

  • •

    f⁢(x)=cos⁡x é uma função par.

  • •

    f⁢(x)=x+1 não é par nem ímpar.

3.8.3 Funções Injetoras

Uma função f é dita ser injetora quando f⁢(x1)≠f⁢(x2) para todos x1≠x2 no seu domínio.

Exemplo 3.8.4.

Estudemos os seguintes casos:

  • •

    f⁢(x)=x2 não é uma função injetora.

  • •

    f⁢(x)=x3 é uma função injetora.

  • •

    f⁢(x)=x−1 é uma função injetora.

Função injetoras são funções invertíveis. Mais precisamente, dada uma função injetora y=f⁢(x), existe uma única função g tal que

g⁢(f⁢(x))=x, (3.145)

para todo x no domínio da f. Tal função g é chamada de função inversa de f é comumente denotada por f−1.3232endnote: 32Atenção! Não confundamos com a função (f⁢(x))−1=1/f⁢(x).

Exemplo 3.8.5.

Vamos calcular a função a função inversa de f⁢(x)=x3+1. Para tando, escrevemos

y=x3+1. (3.146)

Então, isolando x, temos

x=y−13. (3.147)

Desta forma, concluímos que f−1⁢(x)=x−13. Verifique que f−1⁢(f⁢(x))=x para todo x no domínio de f!

Observação 3.8.1.

Os gráficos de uma dada função injetora f e de sua inversa f−1 são simétricos em relação a reta identidade y=x. Use Python e SymPy para verificar esta afirmação plotando os gráficos de f, f−1 e da função identidade!

Exercícios Resolvidos

ER 3.8.1.

Defina os intervalos em que a função f⁢(x)=−|x+1| é crescente ou decrescente.

Solução.

A função f é uma translação à esquerda, seguida de uma reflexão em torno do eixo das abscissas da função f⁢(x)=|x|. Veja a Figura 3.36.

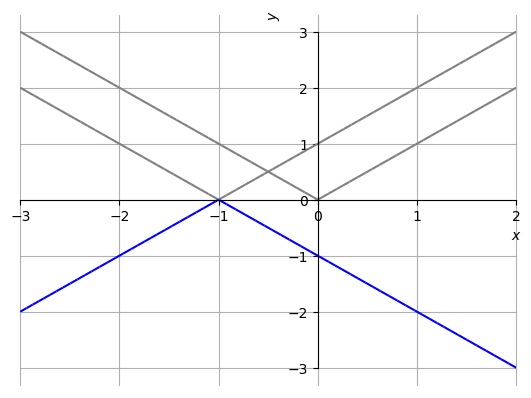
Refer to caption
Figura 3.36: Esboço do gráfico de f⁢(x)=−|x+1|.

Do esboço do gráfico de f, podemos inferir que f é crescente no intervalo (−∞,−1] e decrescente no intervalo [−1,∞).

ER 3.8.2.

Analise a paridade da função t⁢g⁢(x).

Solução.

Da paridade das funções seno e cosseno, temos

tg⁡(−x)=sen⁡(−x)cos⁡(−x)=−sen⁡xcos⁡x=−sen⁡xcos⁡x=−tg⁡x. (3.148)

Logo, a tangente é uma função ímpar.

ER 3.8.3.

Calcule a função inversa de f⁢(x)=x+1.

Solução.

Para obtermos a função inversa de uma função f, resolvemos y=f⁢(x) para x. Ou seja,

y=f⁢(x) ⇒y=x+1 (3.149)
⇒y2=x+1 (3.150)
⇒x=y2−1. (3.151)

Logo, temos f−1⁢(x)=x2−1 restrita ao conjunto imagem da f, i.e. o domínio de f−1 é [0,∞).

Exercícios

E. 3.8.1.

Determine a monotonicidade das seguintes funções:

  1. 1.

    f⁢(x)=1−x

  2. 2.

    g⁢(x)=x2−2⁢x+1

  3. 3.

    h⁢(x)=x5−1

  4. 4.

    f1⁢(x)=−x

  5. 5.

    f2⁢(x)=tg⁡(x)

Resposta.

a) função decrescente; b) função não monótona; c) função crescente; d) função crescente; e) função não monótona

E. 3.8.2.

Determine os intervalos de crescimento ou decrescimento da função

f⁢(x)={(x+1)2,−∞<x≤1,−x+5,1≤x<∞ (3.152)
Resposta.

decrescente: (−∞,−1]∪[1,∞); crescente: [−1,1].

E. 3.8.3.

Analise a paridade da função cosec⁡x.

Resposta.

função ímpar

E. 3.8.4.

Seja f⁢(x)=2⁢x−1−1. Calcule f−1 e determine seu domínio.

Resposta.

f−1⁢(x)=14⁢x2+12⁢x+54; domínio [−1,∞)

E. 3.8.5.

Mostre que toda função crescente (ou decrescente) é uma função injetora.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |