Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Funções 3.6 Funções Trigonométricas 3.8 Propriedades de Funções

3.7 Operações com Funções

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.7.1 Soma , Diferença , Produto e Quociente

Sejam dadas as funções $f$ e $g$ com domínio em comum $D$ . Então, definimos as funções

•

$(f\pm g)(x):=f(x)\pm g(x)$ para todo $x\in D$ ;
•

$(f\cdot g)(x):=f(x)\cdot g(x)$ para todo $x\in D$ ;
•

$\displaystyle\left(\frac{f}{g}\right)(x):=\frac{f(x)}{g(x)}$ para todo $x\in D$ tal que $g(x)\neq 0$ .

Exemplo 3.7.1.

Sejam $f(x)=x^{2}$ e $g(x)=x$ . Temos:

a)

$(f+g)(x)=x^{2}+x$ e está definida em toda parte.
b)

$(g-f)(x)=x-x^{2}$ e está definida em toda parte.
c)

$(f\cdot g)(x)=x^{3}$ e está definida em toda parte.
d)

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{x^{2}}{x}$ e tem domínio $\mathbb{R}\setminus\{0\}$ ³¹³¹endnote: ³¹Observemos que não podemos simplificar o $x$ , pois a função $y=x$ é diferente da função $y=x^{2}/x$ ..

3.7.2 Função Composta

Sejam dadas as funções $f$ e $g$ . Definimos a função composta de $f$ com $g$ por

(f\circ g)(x):=f\left(g(x)\right).

(3.130)

Seu domínio consiste dos valores de $x$ que pertençam ao domínio da $g$ e tal que $g(x)$ pertença ao domínio da $f$ . Em notação matemática

D_{f\circ g}=\{x\in D_{g}:\leavevmode\nobreak\ g(x)\in D_{f}\}

(3.131)

Exemplo 3.7.2.

Sejam $f(x)=x^{2}$ e $g(x)=x+1$ . A função composta de $f$ com $g$ é

	$\displaystyle(f\circ g)(x)$	$\displaystyle=f\left(g(x)\right)$		(3.132)
		$\displaystyle=f(x+1)=(x+1)^{2}$		(3.133)

3.7.3 Translação, Contração, Dilatação e Reflexão de Gráficos

Algumas operações com funções produzem resultados bastante característicos no gráfico de funções. Com isso, podemos usar estas operações para construir gráficos de funções mais complicadas a partir de funções básicas.

3.7.4 Translação

Dada uma função $f$ e uma constante $k\neq 0$ , temos que a o gráfico de $y=f(x)+k$ é uma translação vertical do gráfico de $f$ . Se $k>0$ , observamos uma translação vertical para cima. Se $k<0$ , observamos uma translação vertical para baixo.

Exemplo 3.7.3.

Seja $f(x)=x^{2}$ . A Figura 3.29, contém os esboços dos gráficos de $f(x)$ e $f(x)+k=x^{2}+k$ para $k=1$ .

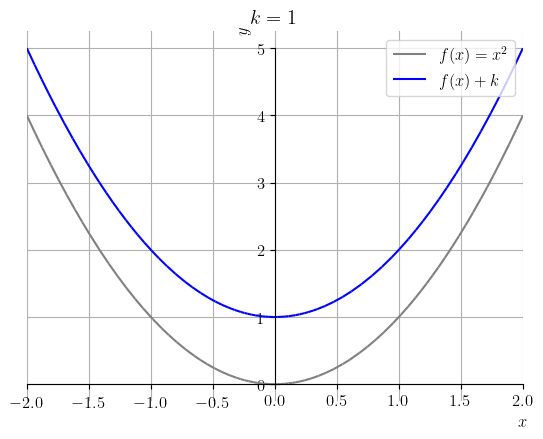
Refer to caption — Figura 3.29: Esboço do gráfico de $f(x)=x^{2}$ e $y=f(x)+k$ com $k=1$ .

O seguinte código Python, faz os esboços dos gráficos de $f(x)$ e $f(x)+k$ :

⬇

1 import matplotlib.pyplot as plt

2 from sympy import *

3 plt.style.use('bmh')

4 x = Symbol('x')

5 k = 1

6 f = Lambda(x, x**2)

7 p = plot(f(x),(x,-2,2),line_color="gray",show=False)

8 q = plot(f(x)+k,(x,-2,2),line_color="blue",show=False)

9 p.extend(q)

10 p.title = (f"$k = {k}$")

11 p.xlabel = '$x$'

12 p.ylabel = '$y$'

13 p[0].label = "$f(x) = x^2$"

14 p[1].label = "$f(x)+k$"

15 p.legend = True

16 p.show()

Alterare o valor de k e a função f para analisar outros casos!

Translações horizontais de gráficos podem ser produzidas pela soma de uma constante não nula ao argumento da função. Mais precisamente, dada uma função $f$ e uma constante $k\neq 0$ , temos que o gráfico de $y=f(x+k)$ é uma translação horizontal do gráfico de $f$ em $k$ unidades. Se $k>0$ , observamos uma translação horizontal para a esquerda. Se $k<0$ , observamos uma translação horizontal para a direita.

Exemplo 3.7.4.

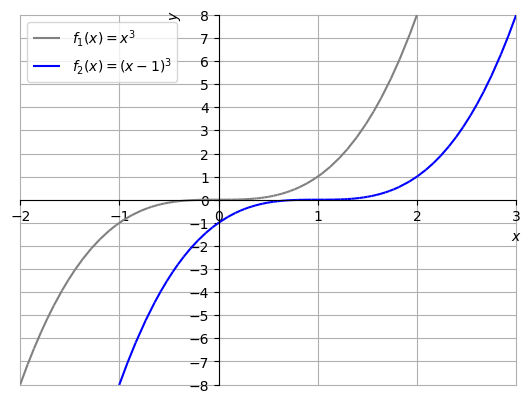
Seja $f(x)=x^{2}$ . A Figura 3.30, contém os esboços dos gráficos de $f(x)$ e $f(x+k)=(x+k)^{2}$ para $k=1$ .

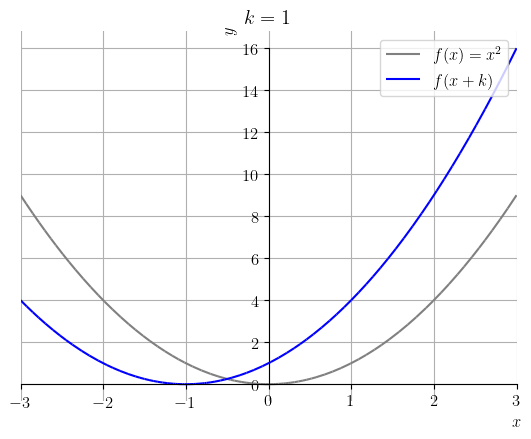
O seguinte código Python, faz os esboços dos gráficos de $f(x)$ e $f(x+k)$ :

⬇

1 import matplotlib.pyplot as plt

2 from sympy import *

3 plt.style.use('bmh')

4 x = Symbol('x')

5 k = 1

6 f = Lambda(x, x**2)

7 p = plot(f(x),(x,-3,3),line_color="gray",show=False)

8 q = plot(f(x+k),(x,-3,3),line_color="blue",show=False)

9 p.extend(q)

10 p.title = (f"$k = {k}$")

11 p.xlabel = '$x$'

12 p.ylabel = '$y$'

13 p[0].label = "$f(x) = x^2$"

14 p[1].label = "$f(x)+k$"

15 p.legend = True

16 p.show()

Altere o valor de k e a função f para analisar outros casos!

3.7.5 Dilatação e Contração

Sejam dadas uma função $f$ e uma constante $\alpha$ . Então, o gráfico de:

•

$y=\alpha f(x)$ é uma dilatação vertical do gráfico de $f$ , quando $\alpha>1$ ;
•

$y=\alpha f(x)$ é uma contração vertical do gráfico de $f$ , quando $0<\alpha<1$ ;
•

$y=f(\alpha x)$ é uma contração horizontal do gráfico de $f$ , quando $\alpha>1$ ;
•

$y=f(\alpha x)$ é uma dilatação horizontal do gráfico de $f$ , quando $0<\alpha<1$ .

Exemplo 3.7.5.

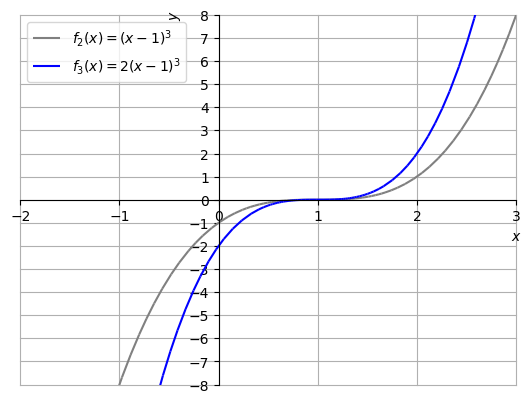
Seja $f(x)=x^{2}$ . A Figura 3.31, contém os esboços dos gráficos de $f(x)$ e $(\alpha\cdot f)(x)=\alpha\cdot x^{2}$ para $\alpha=2$ .

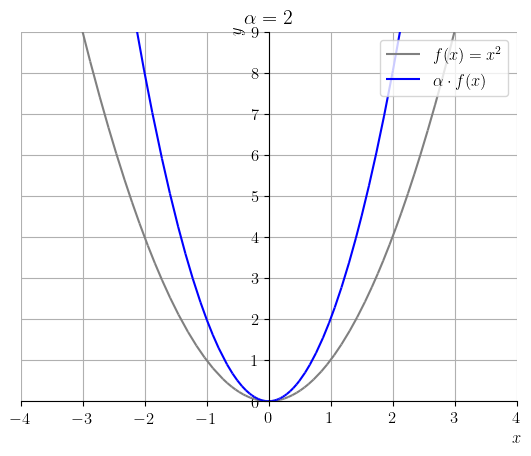
O seguinte código Python, faz os esboços dos gráficos de $f(x)$ e $(\alpha\cdot f)(x)$ :

⬇

1 import matplotlib.pyplot as plt

2 from sympy import *

3 plt.style.use('bmh')

4 x = Symbol('x')

5 alpha = 2

6 f = Lambda(x, x**2)

7 p = plot(f(x),(x,-2,2),line_color="gray",show=False)

8 q = plot(alpha * f(x),(x,-2,2),line_color="blue",show=False)

9 p.extend(q)

10 p.title = (f"$\\alpha = {alpha}$")

11 p.xlabel = '$x$'

12 p.ylabel = '$y$'

13 p[0].label = "$f(x) = x^2$"

14 p[1].label = "$(\\alpha\\cdot f)(x)$"

15 p.legend=True

16 p.show()

Alterare o valor de alpha e a função f para estudar outros casos!

Exemplo 3.7.6.

Seja $f(x)=x^{3}$ . A Figura 3.32, contém os esboços dos gráficos de $f(x)$ e $f(\alpha\cdot x)=(\alpha\cdot x)^{3}$ para $\alpha=\frac{1}{2}$ .

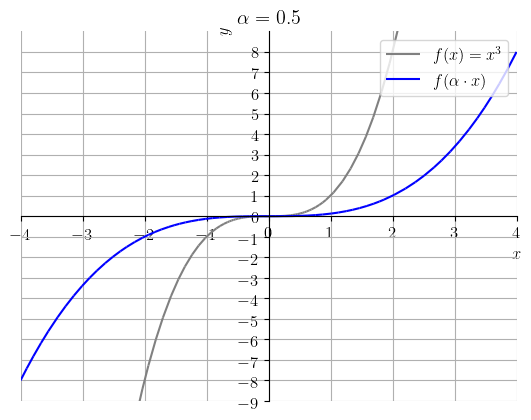
O seguinte código Python, faz os esboços dos gráficos de $f(x)$ e $f(\alpha\cdot x)$ :

⬇

1 import matplotlib.pyplot as plt

2 from sympy import *

3 plt.style.use('bmh')

4 x = Symbol('x')

5 alpha = 0.5

6 f = Lambda(x, x**3)

7 p = plot(f(x),(x,-4,4),ylim=[-9,9],line_color="gray",show=False)

8 q = plot(f(alpha*x),(x,-4,4),ylim=[-9,9],line_color="blue",show=False)

9 p.extend(q)

10 p.title = (f"$\\alpha = {alpha}$")

11 p.xlabel = '$x$'

12 p.ylabel = '$y$'

13 p[0].label = "$f(x) = x^3$"

14 p[1].label = "$f(\\alpha\\cdot x)$"

15 p.legend=True

16 p.show()

Altere o valor de alpha e a função f para estudarmos outros casos!

3.7.6 Reflexão

Seja dada uma função $f$ . O gráfico da função $y=-f(x)$ é uma reflexão em torno do eixo das abscissas do gráfico da função $f$ . Já, o gráfico da função $y=f(-x)$ é uma reflexão em torno do eixo das ordenadas do gráfico da função $f$ .

Exemplo 3.7.7.

Seja $f(x)=x^{2}-2x+2$ . A Figura 3.34, contém os esboços dos gráficos de $f(x)$ e $-f(x)=-x^{2}+2x-2$ .

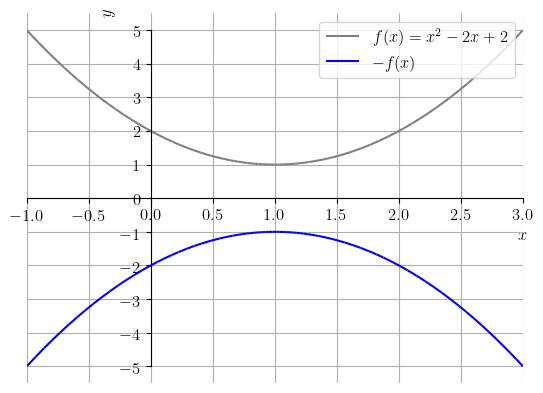
O seguinte código Python, faz os esboços dos gráficos de $f(x)$ e $-f(x)$ :

⬇

1 import matplotlib.pyplot as plt

2 from sympy import *

3 plt.style.use('bmh')

4 x = Symbol('x')

5 f = Lambda(x, x**2-2*x+2)

6 p = plot(f(x),(x,-1,3),ylim=[-5,5],line_color="gray",show=False)

7 q = plot(-f(x),(x,-1,3),ylim=[-5,5],line_color="blue",show=False)

8 p.extend(q)

9 p.xlabel = '$x$'

10 p.ylabel = '$y$'

11 p[0].label = "$f(x)$"

12 p[1].label = "$-f(x)$"

13 p.legend=True

14 p.show()

Altere a função f para estudar outros casos!

Exemplo 3.7.8.

Seja $f(x)=x^{2}-2x+2$ . A Figura LABEL:fig:ex_refley, contém os esboços dos gráficos de $f(x)$ e $f(-x)=x^{2}+2x+2$ .

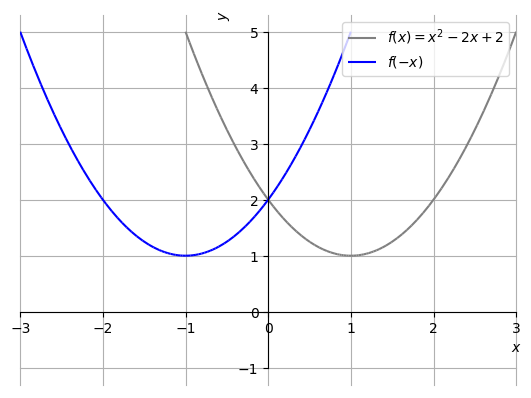
O seguinte código Python, faz os esboços dos gráficos de $f(x)$ e $f(-x)$ :

⬇

1 import matplotlib.pyplot as plt

2 from sympy import *

3 plt.style.use('bmh')

4 x = Symbol('x')

5 f = Lambda(x, x**2-2*x+2)

6 p = plot(f(x),(x,-1,3),line_color="gray",show=False)

7 q = plot(f(-x),(x,-3,1),line_color="blue",show=False)

8 p.extend(q)

9 q = plot(-1,(x,-3,3),line_color="",show=False)

10 p.extend(q)

11 p.xlabel = '$x$'

12 p.ylabel = '$y$'

13 p[0].label = "$f(x)$"

14 p[1].label = "$f(-x)$"

15 p.legend=True

16 p.show()

Altere a função f para estudar outros casos!

Exercícios resolvidos

ER 3.7.1.

Sejam

f(x)=\frac{x^{2}-\sqrt{x-1}}{x}\quad\text{e}\quad g(x)=x^{2}+1.

(3.134)

Determine a função composta $(f\circ g)$ e seu domínio.

Solução.

Começamos determinando a função composta

$\displaystyle(f\circ g)(x)$	$\displaystyle:=f(g(x))$	(3.135)
	$\displaystyle=f(x^{2}+1)$	(3.136)
	$\displaystyle=\frac{(x^{2}+1)^{2}-\sqrt{x^{2}+1-1}}{x^{2}+1}$	(3.137)
	$\displaystyle=\frac{x^{4}+2x^{2}+1-\sqrt{x^{2}}}{x^{2}+1}$	(3.138)
	$\displaystyle=\frac{x^{4}+2x^{2}+1-\|x\|}{x^{2}+1}.$	(3.139)

Agora, observamos que $g$ está definida em toda parte e tem imagem $[1,\infty)$ . Como o domínio da $f$ é $[1,\infty)$ , temos que $(f\circ g)$ está definida em toda parte.

ER 3.7.2.

Faça o esboço do gráfico de $f(x)=2(x-1)^{3}+1$ .

Solução.

Começamos trançando o gráfico de $f_{1}(x)=x^{3}$ . Então, obtemos o gráfico de $f_{2}(x)=(x-1)^{3}$ por translação de uma unidade à direita. O gráfico de $f_{3}(x)=2(x-1)^{3}$ é obtido por dilatação vertical de 2 vezes. Por fim, o gráfico de $f_{4}(x)=2(x-1)^{3}+1$ é obtido por translação de uma unidade para cima. Veja a Figura 3.35.

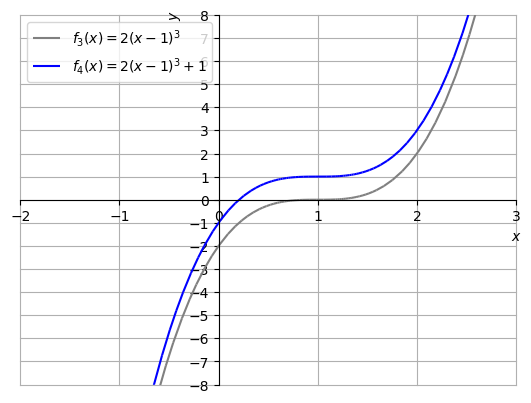
E. 3.7.1.

Determine o domínio e a imagem da função

f(x)=\sqrt{x^{2}-1}

(3.140)

Solução.

A função $f$ é a composição $f=g\circ h(x)$ das funções

	$\displaystyle g(x)=\sqrt{x}$		(3.141)
	$\displaystyle h(x)=x^{2}-1$		(3.142)

A $g$ têm domínio $D(g)=(0,\infty)$ , enquanto que a $h$ está definida em toda parte. Logo, para estar no domínio da $f$ , precisamos que $h(x)\geq 0$ , i.e.

x^{2}-1\geq 0

(3.143)

Fazendo o estudo de sinal da função $h$ , concluímos que $h(x)$ é positiva no conjunto $(-\infty,-1]\cup[1,\infty)$ . Concluímos que o domínio da função $f$ é $D(f)=\{x\in\mathbb{R}:\leavevmode\nobreak\ x\not\in(-1,1)\}$ .

Exercícios

E. 3.7.2.

Dadas as funções $f(x)=x^{2}+2x$ e $g(x)=\frac{1}{x^{2}-1}$ . Determine as seguintes funções e forneça seus respectivos domínios.

a)

$(f+g)(x)$
b)

$(f-g)(x)$
c)

$(f\cdot g)(x)$
d)

$(f\div g)(x)$

Resposta.

a) $\displaystyle(f+g)(x)=\frac{x^{4}-x^{2}+2x^{3}-2x+1}{x^{2}-1}$ , $D=\mathbb{R}\setminus{-1,1}$ ; b) $\displaystyle(f+g)(x)=\frac{x^{4}-x^{2}+2x^{3}-2x-1}{x^{2}-1}$ , $D=\mathbb{R}\setminus{-1,1}$ ; c) $\displaystyle(f\cdot g)(x)=\frac{x^{2}+2x}{x^{2}-1}$ , $D=\mathbb{R}\setminus{-1,1}$ ; d) $\displaystyle(f\div g)(x)=x^{4}-x^{2}+2x^{3}-2x$ , $D=\mathbb{R}\setminus\{-1,1\}$ .

E. 3.7.3.

Seja $f(x)=2^{x}-\sqrt{x-1}+x^{3}$ . Escreva a regra e determine o domínio das seguintes funções:

a)

$f(x)+1$
b)

$2\cdot f(x)$
c)

$f(2x)$
d)

$f(-x)$

Resposta.

a) $f(x)+1=2^{x}-\sqrt{x-1}+x^{3}+1$ , $D=[1,\infty)$ ; b) $2f(x)=2^{x+1}-2\sqrt{x-1}+2x^{3}$ , $D=[1,\infty)$ ; c) $f(2x)=4^{x}-\sqrt{2x-1}+2^{3}x^{3}$ , $D=[\frac{1}{2},\infty)$ ; d) $f(-x)=2^{-x}-\sqrt{-x-1}-x^{3}$ , $D=(-\infty,-1]$

E. 3.7.4.

Sejam $f(x)=\sqrt{x}+1$ e $g(x)=x^{2}-1$ . Determine a função $(f\circ g)$ e seu domínio.

Resposta.

$(f\circ g)(x)=\sqrt{x^{2}-1}+1$ ; domínio: $(-\infty,1]\cup[1,\infty)$ .

E. 3.7.5.

Faça um esboço do gráfico de $g(x)=2x^{3}-1$ .

Resposta.

Dica: verifique sua resposta usando Python e SymPy.

E. 3.7.6.

Faça um esboço do gráfico de $h(x)=-1/(x^{2}+2x+1)$ .

Resposta.

Dica: verifique sua resposta usando Python e SymPy.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |