Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Funções 3.1 Definição e Gráfico de Funções 3.3 Função Potência

3.2 Função Afim

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Uma função afim é uma função da forma

f(x)=mx+b,

(3.30)

sendo $m$ e $b$ parâmetros²³²³endnote: ²³números reais. dados. O parâmetro $m$ é chamado de coeficiente angular e o parâmetro $b$ é chamado de coeficiente constante²⁴²⁴endnote: ²⁴Mais corretamente, coeficiente do termo constante..

Quando $m=0$ , temos uma função constante $f(x)=b$ . Esta tem domínio $(-\infty,\infty)$ e imagem $\{b\}$ . Quando $b=0$ , temos uma função linear $f(x)=mx$ , cujo domínio é $(-\infty,\infty)$ e imagem é $(-\infty,\infty)$ .

De forma geral, toda função linear com $m\neq 0$ tem $(-\infty,\infty)$ como domínio e imagem.

Exemplo 3.2.1.

A Figura 3.5 mostra esboços dos gráficos das funções afins $f(x)=-5/2$ , $f(x)=2$ e $f(x)=2x-1$ .

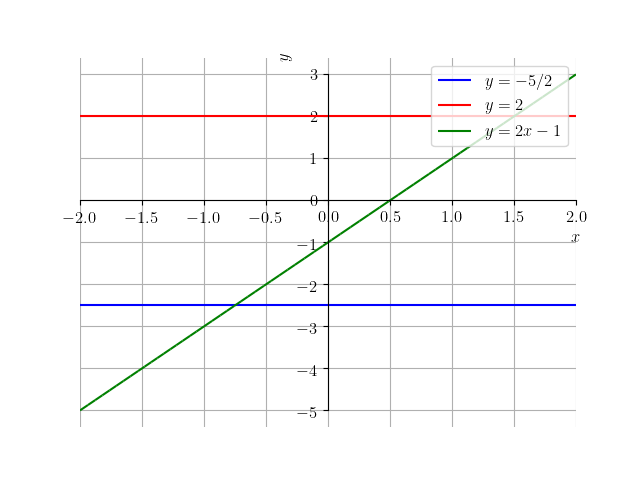
Refer to caption — Figura 3.5: Esboços dos gráficos das funções afins $y=-5/2$ , $y=2$ e $y=2x-1$ discutidas no Exemplo 3.2.1.

Com o SymPy, podemos plotar o gráfico mostrado na Figura 3.5 com o seguinte código:

⬇

1 from sympy import *

2 x = Symbol('x')

3 p = plot(-5/2, (x,-2,2), line_color="blue", show=False)

4 q = plot(2, (x,-2,2), line_color="red", show=False)

5 p.extend(q)

6 q = plot(2*x-1, (x,-2,2), line_color="green", show=False)

7 p.extend(q)

8 p[0].label = "$y=-5/2$"

9 p[1].label = "$y=2$"

10 p[2].label = "$y=$"

11 p.legend = True

12 p.show()

O lugar geométrico do gráfico de uma função afim é uma reta (ou linha). O coeficiente angular $m$ controla a inclinação da reta em relação ao eixo $x$ ²⁵²⁵endnote: ²⁵eixo das abscissas. Quando $m=0$ , temos uma reta horizontal. Quando $m>0$ temos uma reta com inclinação positiva (crescente) e, quando $m<0$ temos uma reta com inclinação negativa.

Exemplo 3.2.2.

A Figura 3.6 mostra esboços dos gráficos das funções lineares $f_{1}(x)=\frac{1}{2}x$ , $f_{2}(x)=x$ , $f_{3}(x)=2x$ , $f_{4}(x)=-2x$ , $f_{5}(x)=-x$ e $f_{6}(x)=-\frac{1}{2}x$ .

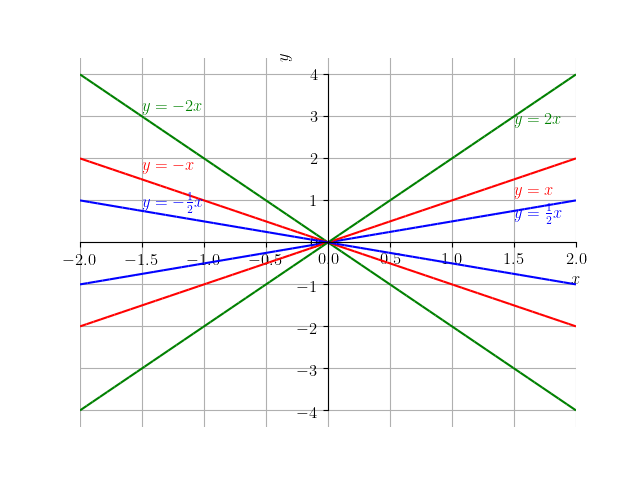
Verifique, plotando os gráficos com o SymPy!

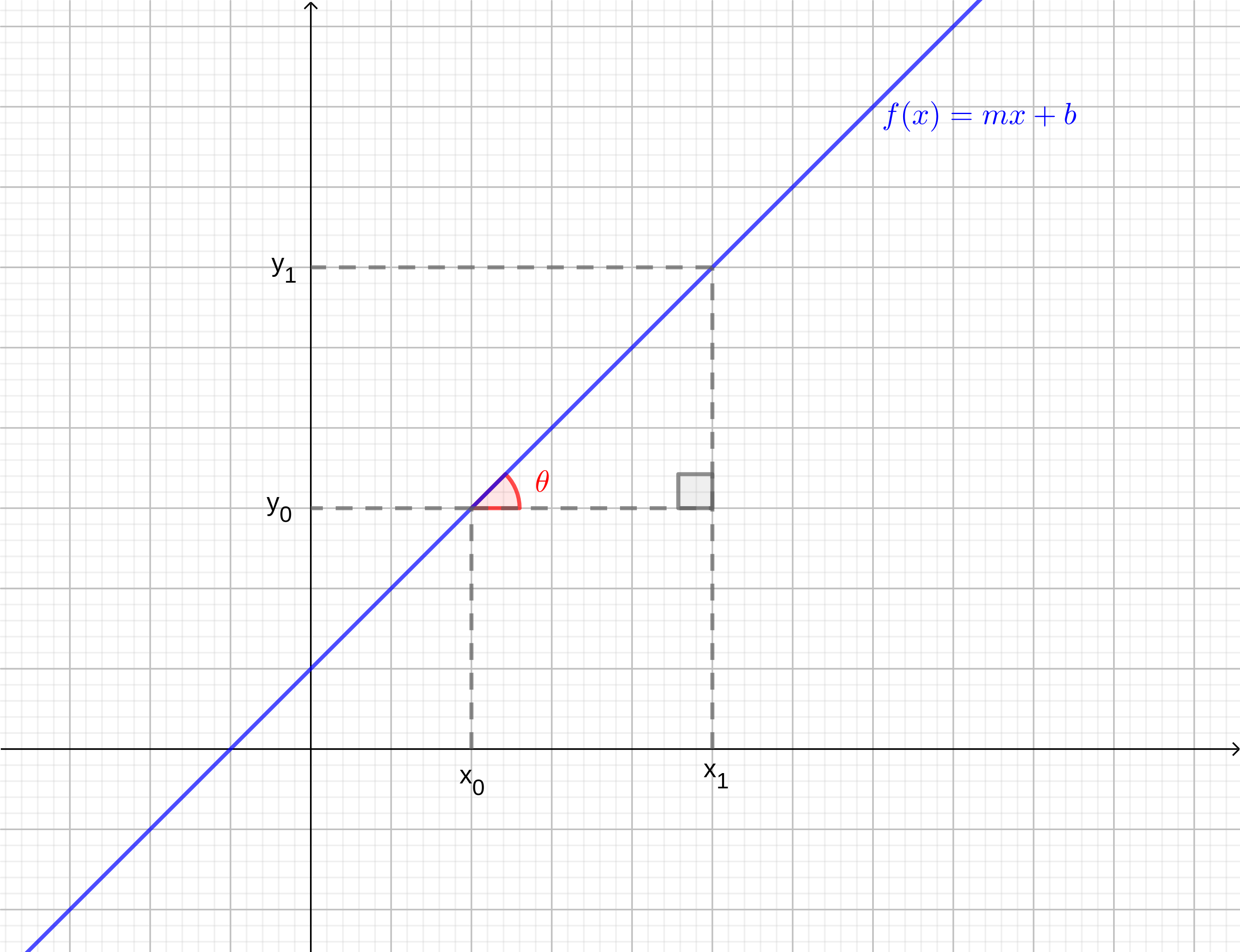
A inclinação de uma reta é, normalmente, medida pelo ângulo de declividade (veja a Figura 3.7). Para definirmos este ângulo, sejam $(x_{0},y_{0})$ e $(x_{1},y_{1})$ , $x_{0}<x_{1}$ , pontos sobre uma dada reta, gráfico da função afim $f(x)=mx+b$ . O ângulo de declividade (ou, simplesmente, a declividade) da reta é, por definição, o ângulo formado pelo segmento que parte de $(x_{0},y_{0})$ e termina em $(x_{1},y_{0})$ e o segmento que parte de $(x_{0},y_{0})$ e termina em $(x_{1},y_{1})$ . Denotando este ângulo por $\theta$ , temos

$\displaystyle\operatorname{tg}\theta$	$\displaystyle=\frac{\text{cateto oposto}}{\text{cateto adjacente}}$	(3.31)
	$\displaystyle=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}$	(3.32)
	$\displaystyle=\frac{mx_{1}+b-(mx_{0}+b)}{x_{1}-x_{0}}$	(3.33)
	$\displaystyle=m,$	(3.34)

o que justifica chamar $m$ de coeficiente angular.

Quaisquer dois pontos $(x_{0},y_{0})$ e $(x_{1},y_{1})$ , com $x_{0}\neq x_{1}$ , determinam uma única função afim (reta) que passa por estes pontos. Para encontrar a expressão desta função, basta resolver o seguinte sistema linear

	$\displaystyle mx_{0}+b$	$\displaystyle=y_{0}$		(3.35)
	$\displaystyle mx_{1}+b$	$\displaystyle=y_{1}$		(3.36)

Subtraindo a primeira equação da segunda, obtemos

	$\displaystyle m(x_{0}-x_{1})=y_{0}-y_{1}$		(3.37)
	$\displaystyle m=\frac{y_{0}-y_{1}}{x_{0}-x_{1}}$		(3.38)

Daí, substituindo o valor de $m$ na primeira equação do sistema, obtemos

	$\displaystyle\frac{y_{0}-y_{1}}{x_{0}-x_{1}}x_{0}+b=y_{0}$		(3.39)
	$\displaystyle b=-\frac{y_{0}-y_{1}}{x_{0}-x_{1}}x_{0}+y_{0}$		(3.40)

Ou seja, a expressão da função linear (equação da reta) que passa pelos pontos $(x_{0},y_{0})$ e $(x_{1},y_{1})$ é

y=\underbrace{\frac{y_{0}-y_{1}}{x_{0}-x_{1}}}_{m}(x-x_{0})+y_{0}.

(3.41)

Exemplo 3.2.3.

Vamos traçar o esboço da reta que representa o gráfico da função afim $f(x)=-x-1$ . Para tanto, basta traçarmos a reta que passa por quaisquer dois pontos distintos de seu gráfico. Por exemplo, no caso da função $f(x)=-x-1$ , temos

$x$	$y=-x-1$
-1	0
1	-2

Assim sendo, marcamos os pontos $(-1,0)$ e $(1,-2)$ em um plano cartesiano e traçamos a reta que passa por eles. Veja a Figura 3.8.

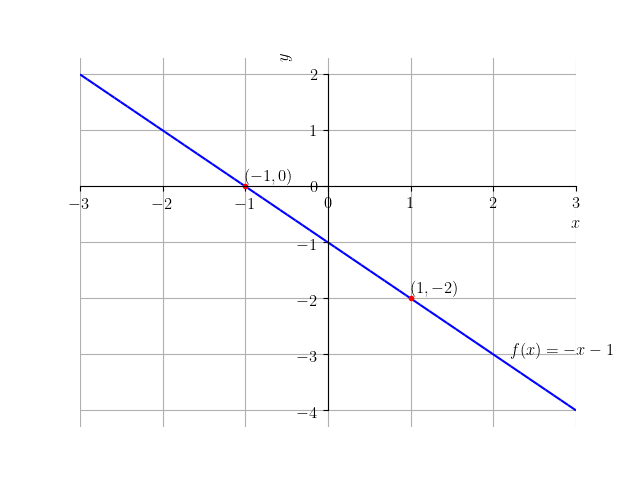
Plote o gráfico com o SymPy e compare com o seu esboço!

Exemplo 3.2.4.

Vamos determinar a função afim $f(x)=mx+b$ , cujo gráfico contém os pontos $(1,-1)$ e $(2,1)$ . Para tanto, vamos usar (3.41). Tomamos

	$\displaystyle(x_{0},y_{0})=(1,-1)$		(3.42)
	$\displaystyle(x_{1},y_{1})=(2,1)$		(3.43)

Então, substituindo em (3.41) temos

m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{1-(-1)}{2-1}=2.

(3.44)

De (3.41), temos

$\displaystyle f(x)$	$\displaystyle=m(x-x_{0})+y_{0}$	(3.45)
	$\displaystyle=2(x-1)+(-1)$	(3.46)
	$\displaystyle=2x-3.$	(3.47)

Ou seja, a função afim desejada é $f(x)=2x-3$ .

Com o SymPy, podemos resolver este exercício utilizando o seguinte código:

from sympy import *
x = Symbol(’x’)
x0 = 1
y0 = -1
x1 = 2
y1 = 1
m = (y1-y0)/(x1-x0)
f = Lambda(x, m*(x-x0) + y0)
print(f"f(x) = {f(x)}")

Exercícios resolvidos

ER 3.2.1.

Faça o estudo de sinal da função

f(x)=2x+1

(3.48)

Solução.

O estudo de sinal de uma função consiste em determinar as regiões de seu domínio em que seus valores de saída são negativos, zero ou positivos. Lembramos que uma função afim com coeficiente angular positivo é crescente em toda parte. Ainda, temos que ela corta o eixo das abscissas em sua raiz, i.e.

	$\displaystyle 2x+1=0$		(3.49)
	$\displaystyle 2x=-1$		(3.50)
	$\displaystyle x=-\frac{1}{2}$		(3.51)

Por tanto, concluímos que

	$x<-\frac{1}{2}$	$x=-\frac{1}{2}$	$x>-\frac{1}{2}$
$f(x)$	-	0	+

Ou seja, $f(x)$ é negativo para $x\in(-\infty,-\frac{1}{2})$ , $f(x)=0$ para $x=-\frac{1}{2}$ e $f(x)$ é positivo para $x\in(-\frac{1}{2},\infty)$ . Faça o esboço do gráfico de $f$ para verificar o resultado!

ER 3.2.2.

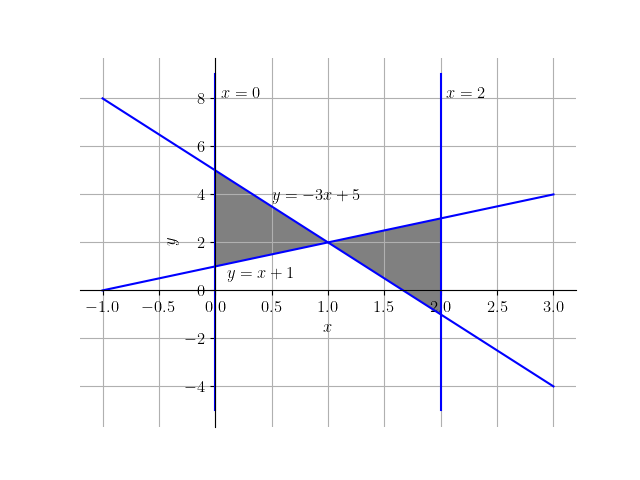
Faça o esboço e hachure a região do plano cartesiano delimitada pelas retas $y=x+1$ , $y=-3x+5$ , $x=0$ e $x=2$ .

Solução.

A reta $y=0$ corresponde ao eixo das ordenadas e $y=2$ é a reta perpendicular ao eixo das abscissas que passa pelo ponto $(2,0)$ . Fazemos os esboços das retas em um único gráfico e então identificamos a região que está simultaneamente entre todas as retas dadas. Obtemos, assim, o gráfico abaixo.

Exercícios

E. 3.2.1.

Determine o domínio e a imagem de cada uma das seguintes funções afins:

a)

$f(x)=-100x+1$
b)

$y=-\pi$
c)

$h(v)=2+x$

Resposta.

a) $D=\mathbb{R}$ ; $I=\mathbb{R}$ ; b) $D=\mathbb{R}$ , $I=\{\pi\}$ ; c) $D=\mathbb{R}$ ; $I=\mathbb{R}$

E. 3.2.2.

Faça um esboço do gráfico de cada uma das seguintes funções:

a)

$f_{1}(x)=x$
b)

$f_{2}(x)=-x$
c)

$f_{3}(x)=x-1$
d)

$f_{4}(x)=-x+1$

E. 3.2.3.

Determine a função afim $f(x)=mx+b$ , cujo gráfico contém os pontos $(-2,1)$ e $(0,-2)$ .

Resposta.

$f(x)=-\frac{3}{2}x-2$

E. 3.2.4.

Faça o estudo de sinal das seguintes funções:

a)

$f(x)=-2x-2$
b)

$f(x)=-2$
c)

$f(x)=2x-2$

Resposta.

a)

$x<-1$ $x=-1$ $x>-1$

$f(x)$ + 0 -
b)

$f(x)<0$ em toda parte
c)

$x<1$ $x=1$ $x>1$

$f(x)$ - 0 +

	$x<-1$	$x=-1$	$x>-1$
$f(x)$	+	0	-

	$x<1$	$x=1$	$x>1$
$f(x)$	-	0	+

E. 3.2.5.

Verifique se as retas $y=-x-1$ e $y=2x-3$ se interceptam e, caso afirmativo, determine o ponto de interseção.

Resposta.

$(2/3,-5/3)$

E. 3.2.6.

Determine o ponto de interseção dos gráficos das funções afins $f(x)=2x+1$ e $g(x)=2x-1$ .

Resposta.

não há

E. 3.2.7.

Faça o esboço e hachure a região do plano cartesiano que fica delimitada pelas retas $y=0$ , $y=2x+2$ e $x=1$ .

E. 3.2.8.

(Aplicação.) Na mecânica clássica, a energia cinética $E_{c}$ de um objeto não rotativo de massa $m$ [kg] movimentando-se com uma velocidade $v$ [ $\text{m}/\text{s}$ ] é dada por

E_{c}=\frac{m}{2}v^{2}

(3.52)

Assumindo $v>0$ constante, temos que $E_{c}$ é função apenas de $m$ , i.e. $E_{c}=E_{c}(m)$ . Responda cada um dos seguintes itens:

a)

Qual a classe da função $E_{c}=E_{c}(m)$ ?
b)

Qual o domínio da função $E_{c}=E_{c}(m)$ .
c)

Qual a imagem da função $E_{c}=E_{c}(m)$ .
d)

$E_{c}=E_{c}(m)$ é uma função crescente ou decresce?
e)

Se $E_{c}(1)=50$ , qual a velocidade do objeto?

Resposta.

a) Função linear. b) $D(E_{v})=\{m\in\mathbb{R}:\leavevmode\nobreak\ m\geq 0\}$ . c) $Im(E_{v})=\{e\in\mathbb{R}:e\geq 0\}$ . d) Sim. Valor mínimo $E_{c}=0$ . Ponto de mínimo $v=0$ . d) Crescente. e) $v=10$ .

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |