Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Funções 3.5 Função Racional 3.7 Operações com Funções

3.6 Funções Trigonométricas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Funções trigonométricas são funções transcendentes e são construídas a partir do estudo trigonométrico de triângulos retângulos.

3.6.1 Seno e Cosseno

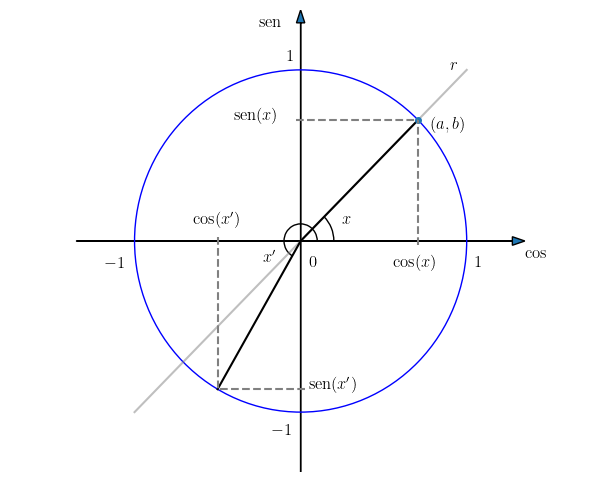
As funções trigonométricas seno $y=\operatorname{sen}(x)$ e cosseno $y=\cos(x)$ podem ser definidas a partir do círculo trigonométrico (veja a Figura 3.21). Seja $x$ o ângulo²⁷²⁷endnote: ²⁷Em geral utilizaremos a medida em radianos para ângulos. de declividade da reta que passa pela origem do plano cartesiano (reta $r$ na Figura 3.21). Seja, então, $(a,b)$ o ponto de interseção desta reta com a circunferência unitária²⁸²⁸endnote: ²⁸Circunferência do círculo de raio 1.. Então, definimos:

\operatorname{sen}(x)=b,\qquad\cos(x)=a.

(3.100)

A partir da definição, notamos que ambas funções têm domínio $(-\infty,\infty)$ e imagem $[-1,1]$ .

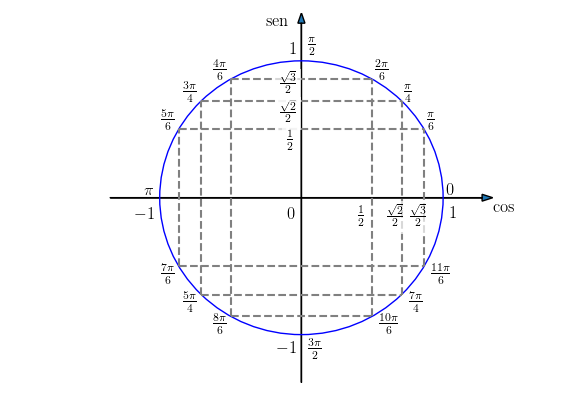
Refer to caption — Figura 3.21: Funções seno e cosseno no círculo trigonométrico.

Na Figura 3.22 podemos extrair os valores das funções seno e cosseno para os ângulos fundamentais. Por exemplo, temos

	$\displaystyle\operatorname{sen}\left(\frac{\pi}{6}\right)=\frac{1}{2},\qquad% \cos\left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2},$		(3.101)
	$\displaystyle\operatorname{sen}\left(\frac{3\pi}{4}\right)=\frac{\sqrt{2}}{2},% \qquad\cos\left(\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2},$		(3.102)
	$\displaystyle\operatorname{sen}\left(\frac{8\pi}{6}\right)=-\frac{\sqrt{3}}{2}% ,\qquad\cos\left(\frac{8\pi}{6}\right)=-\frac{1}{2},$		(3.103)
	$\displaystyle\operatorname{sen}\left(\frac{11\pi}{6}\right)=-\frac{1}{2},% \qquad\cos\left(\frac{11\pi}{6}\right)=\frac{\sqrt{3}}{2},$		(3.104)

As funções seno e cosseno estão definidas no SymPy como sin e $\verb+cos+$ , respectivamente. Por exemplo, para computar o seno de $\pi/6$ , digitamos:

⬇

1 from sympy import *

2 sin(pi/6)

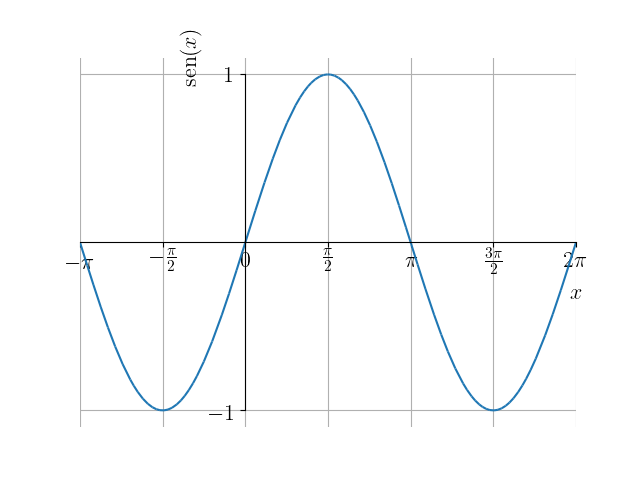
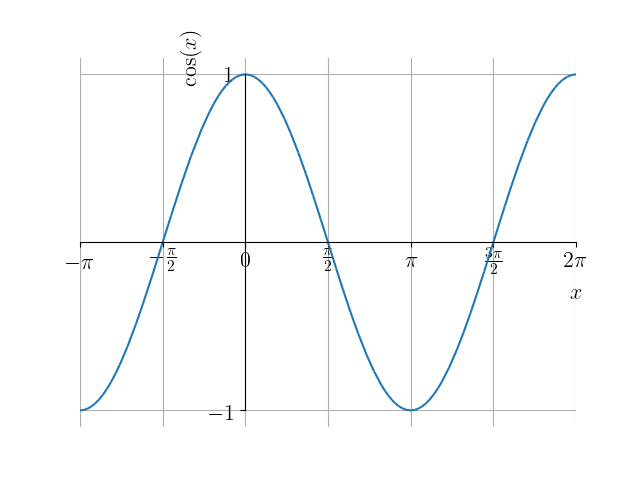
Uma função $f(x)$ é dita periódica quando existe um número $p$ , chamado de período da função, tal que

f(x+p)=f(x)

(3.106)

para qualquer valor de $x$ no domínio da função. Da definição das funções seno e cosseno, observamos que ambas são periódicas com período $2\pi$ , i.e.

\operatorname{sen}(x+2\pi)=\operatorname{sen}(x)

(3.107)

\cos(x+2\pi)=\cos(x)

(3.108)

para qualquer valor de $x$ .

A Figura 3.23 contém o esboço do gráfico da função seno e a Figura 3.24 o da função cosseno.

3.6.2 Tangente, Cotangente, Secante e Cossecante

Das funções seno e cosseno, definimos as funções tangente, cotangente, secante e cossecante como seguem:

	$\displaystyle\operatorname{tg}(x):=\frac{\operatorname{sen}(x)}{\cos(x)}$		(3.109)
	$\displaystyle\operatorname{cotg}(x):=\frac{\cos(x)}{\operatorname{sen}(x)}$		(3.110)
	$\displaystyle\sec(x):=\frac{1}{\cos(x)},$		(3.111)
	$\displaystyle\operatorname{cosec}(x):=\frac{1}{\operatorname{sen}(x)}$		(3.112)

No Python+SymPy, as funções tangente, cotangente, secante e cossecante podem ser computadas com as funções $\verb+tan+$ , $\verb+cot+$ , $\verb+sec+$ e $\verb+csc+$ , respectivamente. Por exemplo, podemos computar o valor de $\operatorname{cosec}(\pi/4)$ com o comando

⬇

1In : from sympy import *

2...: csc(pi/4)

3Out: sqrt(2)

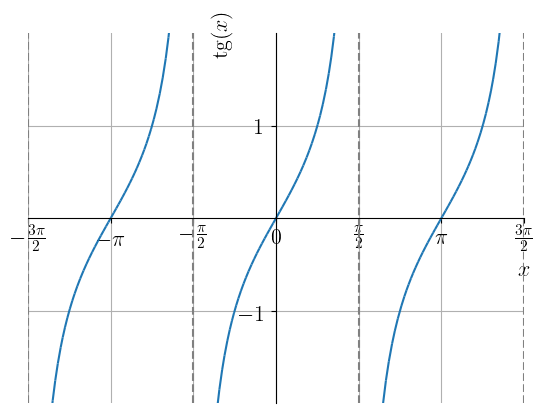
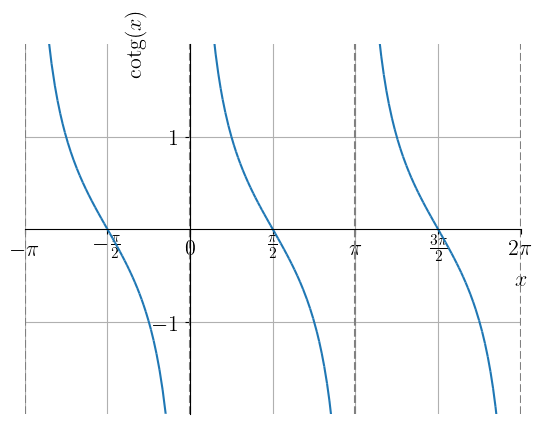
Na Figura 3.25, temos o esboço do gráfico da função tangente e na Figura 3.26 o da cotangente. Observemos que a função tangente não está definida nos pontos $(2k+1)\pi/2$ , para todo $k$ inteiro. Já, a função cotangente não está definida nos pontos $k\pi$ , para todo $k$ inteiro. Ambas estas funções têm imagem $(-\infty,\infty)$ e período $\pi$ .

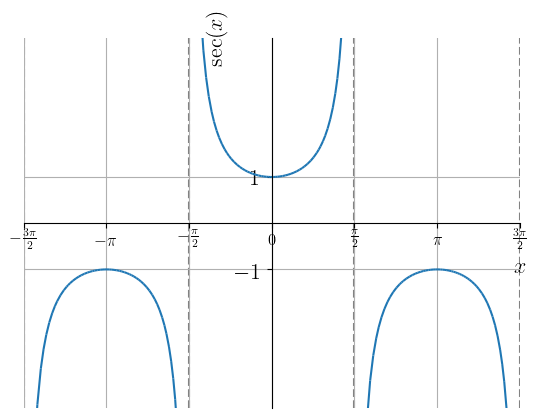
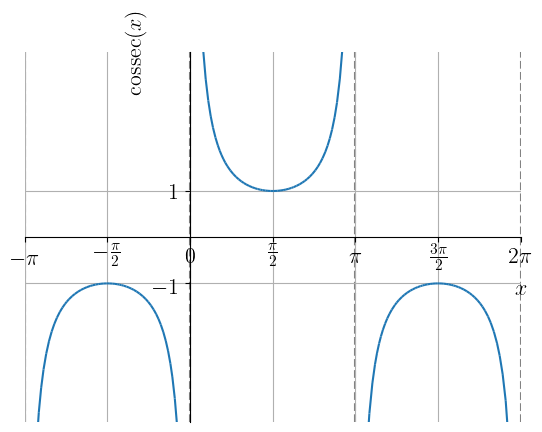
Na Figura 3.27, temos o esboço do gráfico da função secante e na Figura 3.28 o da função cossecante. Observemos que a função secante não está definida nos pontos $(2k+1)\pi/2$ , para todo $k$ inteiro. Já, a função cossecante não está definida nos pontos $k\pi$ , para todo $k$ inteiro. Ambas estas funções têm imagem $(-\infty,1]\cup[1,\infty)$ e período $\pi$ .

3.6.3 Identidades Trigonométricas

Aqui, vamos apresentar algumas identidades trigonométricas que serão utilizadas ao longo do curso de cálculo. Comecemos pela identidade fundamental

\operatorname{sen}^{2}x+\cos^{2}x=1.

(3.113)

Desta decorrem as identidades

	$\displaystyle\operatorname{tg}^{2}(x)+1=\sec^{2}x,$		(3.114)
	$\displaystyle 1+\operatorname{cotg}^{2}(x)=\operatorname{cosec}^{2}(x).$		(3.115)

Das seguintes fórmulas para adição/subtração de ângulos

	$\displaystyle\cos(x\pm y)=\cos(x)\cos(y)\mp\operatorname{sen}(x)\operatorname{% sen}(y),$		(3.116)
	$\displaystyle\operatorname{sen}(x\pm y)=\operatorname{sen}(x)cos(y)\pm\cos(x)% \operatorname{sen}(y),$		(3.117)

seguem as fórmulas para ângulo duplo

	$\displaystyle\cos(2x)=\cos^{2}x-\operatorname{sen}^{2}x,$		(3.118)
	$\displaystyle\operatorname{sen}(2x)=2\operatorname{sen}x\cos x.$		(3.119)

Também, temos as fórmulas para o ângulo metade

	$\displaystyle\cos^{2}x=\frac{1+\cos 2x}{2},$		(3.120)
	$\displaystyle\operatorname{sen}^{2}x=\frac{1-\cos 2x}{2}.$		(3.121)

Exercícios Resolvidos

ER 3.6.1.

Mostre que

\cos x-1=-2\operatorname{sen}^{2}\frac{x}{2}.

(3.122)

Solução.

A identidade trigonométrica

\operatorname{sen}^{2}x=\frac{1-\cos 2x}{2},

(3.123)

aplicada a metade do ângulo, fornece

\operatorname{sen}^{2}\frac{x}{2}=\frac{1-\cos x}{2}.

(3.124)

Então, isolando $\cos x$ , obtemos

	$\displaystyle\operatorname{sen}^{2}\frac{x}{2}=\frac{1-\cos x}{2}$		(3.125)
	$\displaystyle 1-\cos x=2\operatorname{sen}^{2}\frac{x}{2}$		(3.126)
	$\displaystyle\cos x-1=-2\operatorname{sen}^{2}\frac{x}{2}.$		(3.127)

Exercícios

E. 3.6.1.

Calcule os seguintes valores

a)

$\operatorname{sen}(7\pi/6)$
b)

$\cos(7\pi/6)$
c)

$\operatorname{tg}(7\pi/6)$
d)

$\operatorname{cotg}(7\pi/6)$
e)

$\sec(7\pi/6)$
f)

$\operatorname{cosec}(7\pi/6)$

Resposta.

a) $-1/2$ ; b) $-\sqrt{3}/2$ ; c) $\sqrt{3}/3$ ; d) $\sqrt{3}$ ; e) $-2\sqrt{3}/3$ ; f) $-2$

E. 3.6.2.

Calcule os seguintes valores

a)

$\operatorname{sen}(-pi/3)$
b)

$tg(-3\pi/4)$
c)

$\cos(19\pi/6)$

Resposta.

a) $-\sqrt{3}/2$ ; b) $1$ ; c) $-\sqrt{3}/2$

E. 3.6.3.

Mostre que $\operatorname{sen}x$ é uma função ímpar²⁹²⁹endnote: ²⁹Por definição, $f(x)$ é função ímpar quando $f(x)=-f(-x)$ ., i.e.

\operatorname{sen}x=-\operatorname{sen}(-x)

(3.128)

para todo número real $x$ .

Resposta.

Dica: analise o ciclo trigonométrico.

E. 3.6.4.

Mostre que $\cos x$ é uma função par³⁰³⁰endnote: ³⁰Por definição, $f(x)$ é uma função par quando $f(x)=f(-x)$ ., i.e.

\cos x=\cos(-x)

(3.129)

para todo número real $x$ .

Resposta.

Dica: analise o ciclo trigonométrico.

E. 3.6.5.

Determine os pontos de interseção entre as funções $f(x)=2x/\pi$ e $g(x)=\operatorname{sen}(x)$ .

Resposta.

$(-\pi/2,-1)$ , $(0,0)$ , $(\pi/2,1)$

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |