| | | | |

3.6 Produto Misto

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Em revisão

O produto misto de três vetores u→, v→ e w→, nesta ordem, é definido por

[u→,v→,w→]:=u→×v→⋅w→. (3.356)

Em coordenadas, temos

[u→,v→,w→]:=(u→×v→)⋅w→ (3.357)
=|i→j→k→u1u2u3v1v2v3|⋅w→ (3.361)
=(|u2u3v2v3|⁢i→−|u1u3v1v3|⁢j→+|u1u2v1v2|⁢k→)⋅(w1,w2,w3) (3.368)
=|u2u3v2v3|⁢w1−|u1u3v1v3|⁢w2+|u1u2v1v2|⁢w3 (3.375)
=|w1w2w3u1u2u3v1v2v3| (3.379)
=|u1u2u3v1v2v3w1w2w3| (3.383)

Ou seja, temos

[u→,v→,w→]=|u1u2u3v1v2v3w1w2w3| (3.384)
Exemplo 3.6.1.

Dados os vetores u→=(1,−1,0), v→=(1,0,2) e w→=(1,−1,1), temos

[u→,v→,w→] =|u1u2u3v1v2v3w1w2w3| (3.388)
=|1−101021−11| (3.392)
=1 (3.393)

3.6.1 Interpretação Geométrica

Seja (u→,v→,w→) uma sequência de vetores l.i. e com orientação positiva. Assumindo as representações u→=A⁢B→, v→=A⁢D→ e w→=A⁢H→ temos a determinação de um paralelepípedo (consulte a Figura 3.5).

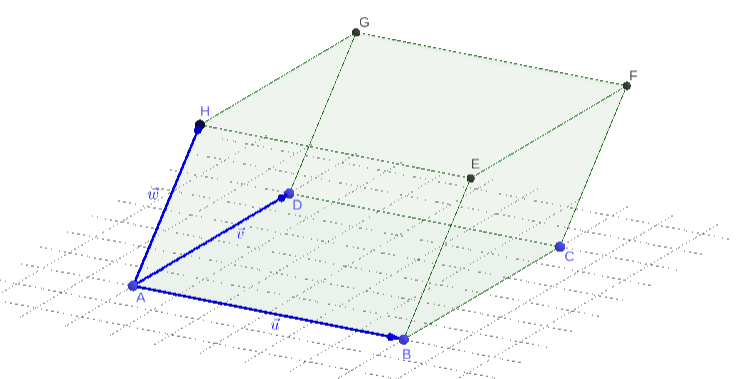
Refer to caption
Figura 3.5: Interpretação geométrica do produto misto.

A base do paralelepípedo é o paralelogramo A⁢B⁢C⁢D de área ‖u→×v→‖. Assim sendo, o volume do paralelepípedo é

V=‖u→×v→‖⋅h, (3.394)

onde h é a altura do prisma. Por sua vez,

h =‖proju→×v→⁡w→‖ (3.395)
=‖w→⋅(u→×v→)‖u→×v→‖2⁢u→×v→‖ (3.396)
=|w→⋅(u→×v→)|‖u→×v→‖2⁢‖u→×v→‖ (3.397)
=|w→⋅(u→×v→)|‖u→×v→‖ (3.398)

Logo, retornando a (3.394), obtemos

V =‖u→×v→‖⋅h (3.399)
=‖u→×v→‖⋅|w→⋅(u→×v→)|‖u→×v→‖ (3.400)
=|w→⋅(u→×v→)| (3.401)
=|u→×v→⋅w→|. (3.402)

Ou seja, o volume do paralelepípedo formado pelos vetores u→, v→ e w→ é igual a norma do produto misto destes vetores, i.e.

V=|[u→,v→,w→]|. (3.403)
Exemplo 3.6.2.

Vamos calcular o volume do paralelepípedo determinado pelos vetores u→=(1,1,0), v→=(−1,2,0) e w→=(0,1,1). De (3.403), temos

V=|[u→,v→,w→]| (3.404)
=||110−120011|| (3.408)
=|3|=3. (3.409)

3.6.2 Propriedades

Valem as seguintes propriedades:

  1. a)

    [u→,v→,w→]=−[v→,u→,w→]

    Demonstração. De fato, quando permutamos duas linhas em uma matriz, seu determinante troca de sinal.

  2. b)

    [u→,v→,w→]=−[u→,w→,v→]

    Demonstração. Mesmo argumento da letra a).

  3. c)

    [u→,v→,w→]=[w→,u→,v→]=[v→,w→,u→]

    Demonstração. De fato, cada caso acima corresponde a duas consecutivas permutações de linha na matriz associada ao produto misto.

  4. d)

    [u→,v→,w→]=u→×v→⋅w→=u→⋅v→×w→

    Demonstração. Isto segue de c), i.e.

    [u→,v→,w→] =[v→,w→,u→] (3.410)
    u→×v→⋅w→ =v→×w→⋅u→ (3.411)
    =u→⋅v→×w→. (3.412)
  5. e)

    [α⁢u→,v→,w→]=[u→,α⁢v→,w→]=[u→,v→,α⁢w→]=α⁢[u→,v→,w→]

    Determinação. De fato, ao multiplicarmos uma linha de uma matriz por um escalar α, seu determinante fica multiplicado por α.

  6. f)

    [u→+z→,v→,w→]=[u→,v→,w→]+[z→,v→,w→]

    Determinante. Também segue da propriedade análoga do determinante de matrizes.

Exemplo 3.6.3.

Sabendo que [u→⁢,2⁢w→,v→]=2, vamos calcular [u→,v→,w→]. Do item e) acima, temos

2 =[u→⁢,2⁢w→,v→] (3.413)
=2⁢[u→,w→,v→], (3.414)

donde

[u→,w→,v→]=1. (3.415)

Agora, do item b), temos

[u→,w→,v→]=−[u→,v→,w→]. (3.416)

Ou seja, concluímos que [u→,v→,w→]=−1.

Também, temos as seguinte propriedades envolvendo o produto misto:

  1. a)

    Se [u→,v→,w→]=0, então (u→,v→,w→) não é base.

    Demonstração. Seja [u→,v→,w→]=0, i.e. u→×v→⋅w→=0. No caso de um dos vetores serem nulos, então (u→,v→,w→) não é base. Suponhamos, então, que u→, v→ e w→ são vetores não nulos. Isso implica que u→×v→=0 ou (u→×v→)⟂w→. No primeiro caso, u→ e v→ são l.d. e, portanto, (u→,v→,w→) não é base. No segundo caso, (u→×v→)⟂w→, temos que w→ é coplanar aos vetores u→ e v→, logo (u→,v→,w→) não é base.

  2. b)

    Se [u→,v→,w→]>0, então (u→,v→,w→) é uma base positiva.

    Demonstração. Se [u→,v→,w→]>0, implica que o ângulo entre u→×v→ e w→ é agudo, o que garante que (u→,v→,w→) seja uma base positiva.

  3. c)

    Se [u→,v→,w→]<0, então (u→,v→,w→) é uma base negativa.

    Demonstração. Se [u→,v→,w→]<0, implica que o ângulo entre u→×v→ e w→ é obtuso, o que garante que (u→,v→,w→) seja uma base negativa.

3.6.3 Exercícios Resolvidos

ER 3.6.1.

Calcule a área do paralelogramo determinado pelos vetores v→=(1,0,−2), w→=(1,−2,1) e u→=(0,2,1).

Solução.

Da Subseção 3.6.1, temos que o volume do paralelogramo é

V=|[u→,v→,w→]|, (3.417)

não importando a ordem dos vetores1919endnote: 19A ordem dos vetores não altera o módulo do valor do produto misto.. Assim sendo, temos

V=|[u→,v→,w→]| (3.418)
=||02110−21−21|| (3.422)
=|−8|=8. (3.423)
ER 3.6.2.

Sejam u→, v→ e w→ vetores dados. Verifique a seguinte afirmação:

[u→,v→+α⁢u→+β⁢w→,w→]=[u→,v→,w→], (3.424)

onde α e β são quaisquer escalares.

Solução.

Das propriedades do produto misto2020endnote: 20[u→,v→+z→,w→]=[u→,v→,w→]+[u→,z→,w→]., temos

[u→,v→+α⁢u→+β⁢w→,w→] (3.425)
=[u→,v→,w→]+[u→,α⁢u→+β⁢w→,w→]. (3.426)

Agora, observamos que α⁢u→+β⁢w→ é combinação linear de u→ e v→, logo (u→,α⁢u→+β⁢w→,w→) é l.d. e, portanto,

[u→,α⁢u→+β⁢w→,w→]=0. (3.427)

Concluímos que

[u→,v→+α⁢u→+β⁢w→,w→]=[u→,v→,w→]. (3.428)

3.6.4 Exercícios

E. 3.6.1.

Calcule [u→,v→,w→] sendo u→=(−1,0,1), v→=(1,3,0) e w→=(1,−2,−1).

Resposta.

-2

E. 3.6.2.

Sejam a→=(0,0,2), d→=(−1,1,1) e e→=(1,1,1). Calcule [d→,a→,e→].

Resposta.

4

E. 3.6.3.

Sendo [u→,v→,w→]=2, calcule [2⁢u→,−3⁢v→,w→].

Resposta.

−12

E. 3.6.4.

Sendo [u→,v→,w→]=2, calcule [2⁢u→−5⁢w→,−3⁢v→,w→].

Resposta.

−12

E. 3.6.5.

Sejam u→=(0,x⁢,2), v→=(−1,1,1) e w→=(1,1,1). Calcule x de forma que [u→,v→,w→]=2.

Resposta.

3

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |