Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Produtos 3.3 Projeção Ortogonal 3.5 Propriedades do Produto Vetorial

3.4 Produto Vetorial

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Em revisão

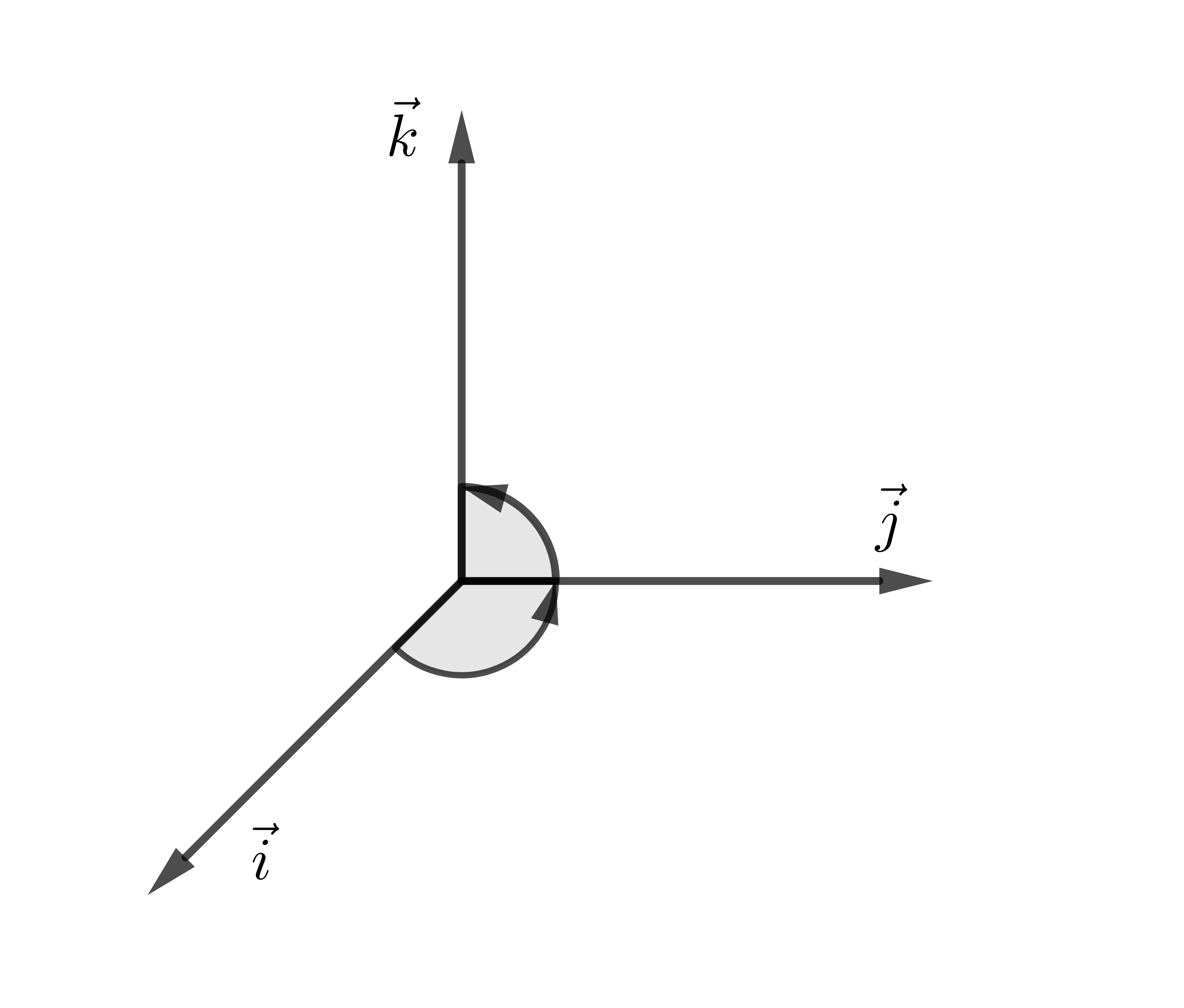
De agora em diante, vamos trabalhar com um base ortonormal $B=(\vec{i},\vec{j},\vec{k})$ dita com orientação positiva, i.e. os vetores $\vec{i}=\overrightarrow{OI}$ , $\vec{j}=\overrightarrow{OJ}$ e $\vec{k}=\overrightarrow{OK}$ estão dispostos em sentido anti-horário, veja Figura 3.3.

Refer to caption — Figura 3.3: Base ortonormal com orientação positiva.

Dados vetores $\vec{u}$ e $\vec{v}$ , definimos o produto vetorial de $\vec{u}$ com $\vec{v}$ , por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{u}\times% \vec{v}=\|\vec{u}\|\|\vec{v}\|\operatorname{sen}(\alpha)\vec{n},

(3.136)

onde $\theta$ é ângulo entre $\vec{u}$ e $\vec{v}$ , e $\vec{n}$ é o vetor unitário ortogonal ao plano determinado por $\vec{u}$ e $\vec{v}$ , e com sentido tal que $(\vec{u},\vec{v},\vec{n})$ tem orientação positiva.

Em outras palavras, temos que:

•

se $\vec{u}$ e $\vec{v}$ são l.d., então $\vec{u}\times\vec{v}=\vec{0}$ .
•
se $\vec{u}$ e $\vec{v}$ são l.i., então
- a)
  
  $\|\vec{u}\times\vec{v}\|=\|\vec{u}\|\|\vec{v}\|\operatorname{sen}\alpha$ , onde $\alpha$ é o ângulo entre $\vec{u}$ e $\vec{v}$ ,
- b)
  
  $\vec{u}\times\vec{v}$ é ortogonal a $\vec{u}$ e $\vec{v}$ , e
- c)
  
  $\vec{u}$ , $\vec{v}$ e $\vec{u}\times\vec{v}$ formam uma base positiva.

3.4.1 Interpretação Geométrica

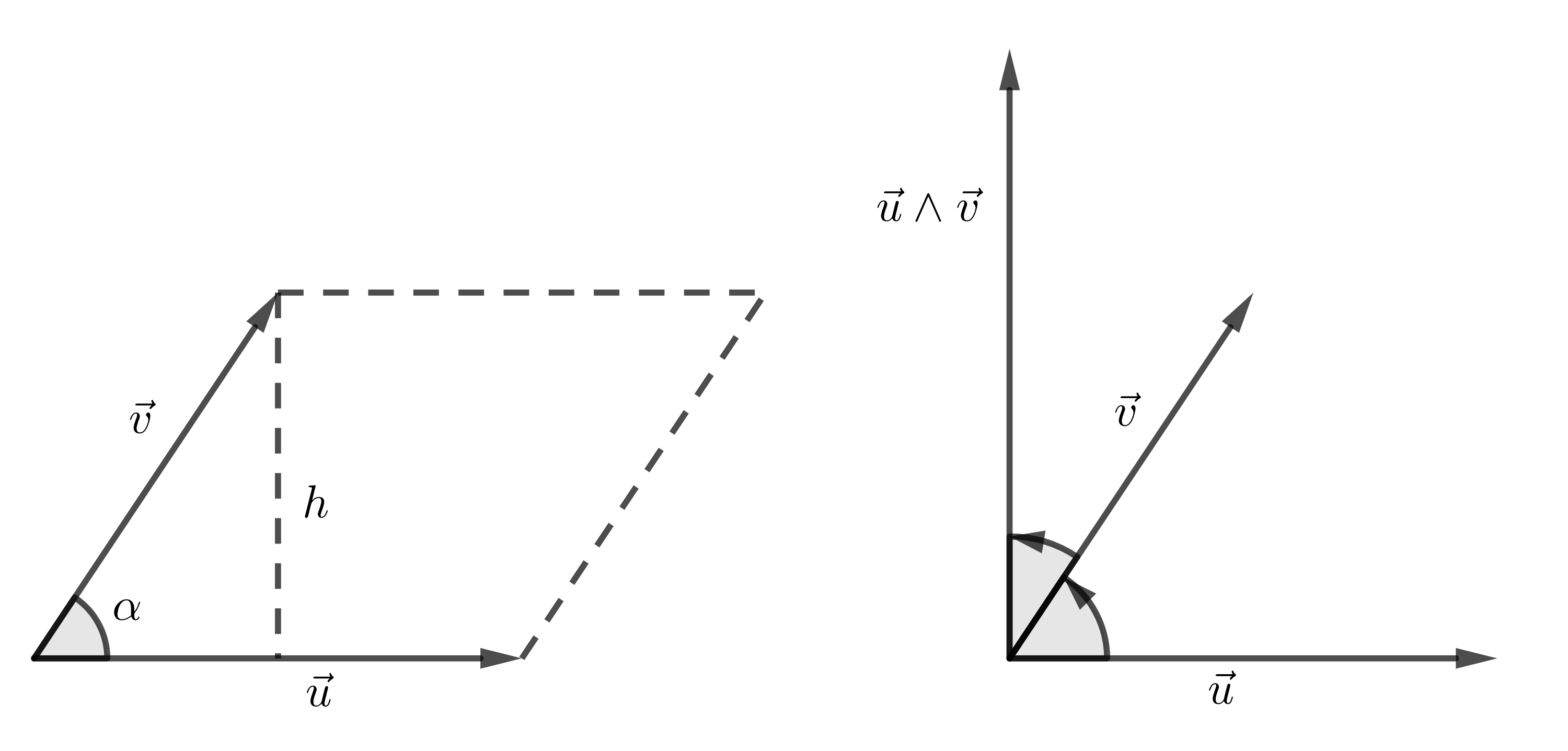
Sejam dados $\vec{u}$ e $\vec{v}$ l.i.. Estes vetores determinam um paralelogramo (consulte Figura 3.4 (esquerda)). Seja, então, $h$ a altura deste paralelogramo tendo $\vec{u}$ como sua base. Logo, a área do paralelogramo é o produto do comprimento da base com sua altura, neste caso

	$\displaystyle\\|\vec{u}\\|h$	$\displaystyle=\\|\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\alpha)$		(3.137)
		$\displaystyle=\\|\vec{u}\times\vec{v}\\|.$		(3.138)

Ou seja, o produto vetorial $\vec{u}\times\vec{v}$ tem norma igual à área do paralelogramo determinado por $\vec{u}$ e $\vec{v}$ .

Ainda, por definição, $\vec{u}\times\vec{v}$ é ortogonal a $\vec{u}$ e $\vec{v}$ . Isto nos dá a direção de $\vec{u}\times\vec{v}$ . O sentido é, então, determinado pela definição de que $(\vec{u},\vec{v},\vec{u}\times\vec{v})$ tem orientação positiva. Consulte a Figura 3.4 (direita).

3.4.2 Vetores Canônicos

Vamos ver alguns resultados fundamentais envolvendo o produto vetorial de vetores da base canônica.

•

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{i}\times% \vec{i}=\vec{j}\times\vec{j}=\vec{k}\times\vec{k}=\vec{0}$

Segue, imediatamente, da definição de que é nulo o produto vetorial de vetores l.i..
•

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{i}\times% \vec{j}=\vec{k}$ , $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{j}\times% \vec{k}=\vec{i}$ , $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{k}\times% \vec{i}=\vec{j}$

No primeiro caso, temos

$\displaystyle\vec{i}\times\vec{j}$ $\displaystyle:=\|\vec{i}\|\|\vec{j}\|\operatorname{sen}(\alpha)\vec{n}$ (3.139)

$\displaystyle=1\cdot 1\cdot\operatorname{sen}\left(\frac{\pi}{2}\right)\vec{k}$ (3.140)

$\displaystyle=\vec{k}.$ (3.141)

Análogo para os outros casos. Consulte o E.3.4.1.
•

$\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{j}\times% \vec{i}=-\vec{k}$ , $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{k}\times% \vec{j}=-\vec{i}$ , $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{i}\times% \vec{k}=-\vec{j}$

No primeiro, temos

$\displaystyle\vec{j}\times\vec{i}$ $\displaystyle:=\|\vec{j}\|\|\vec{i}\|\operatorname{sen}(\theta)\vec{n}$ (3.142)

$\displaystyle=1\cdot 1\cdot\operatorname{sen}\left(\frac{\pi}{2}\right)(-\vec{% k})$ (3.143)

$\displaystyle=-\vec{k}.$ (3.144)

Análogo para os outros casos. Consulte o E.3.4.3.

Distributividade

A propriedade de distributividade do produto vetorial com vetores da base canônica também pode ser mostrada. Por exemplo, é verdade que

\vec{i}\times(\vec{j}+\vec{k})=\vec{i}\times\vec{j}+\vec{i}\times\vec{k}.

(3.145)

De fato, assumindo $\vec{n}$ o vetor normal unitário aos vetores $\vec{i}$ e $\vec{j}+\vec{k}$ , temos

	$\displaystyle\vec{i}\times(\vec{j}+\vec{k})$	$\displaystyle:=\\|\vec{i}\\|\\|\vec{j}+\vec{k}\\|\operatorname{sen}\left(\frac{\pi% }{2}\right)\vec{n}$		(3.146)
		$\displaystyle=1\cdot\sqrt{2}\cdot 1\vec{n}=\sqrt{2}\vec{n}.$		(3.147)

Por outro lado, temos

\displaystyle\vec{i}\times\vec{j}+\vec{i}\times\vec{k}=\vec{k}-\vec{j}

(3.148)

Seria, então,

\vec{n}\stackrel{{\scriptstyle?}}{{=}}\frac{\sqrt{2}}{2}\vec{k}-\frac{\sqrt{2}% }{2}\vec{j}

(3.149)

De fato, enquanto a positividade de $(\vec{i},\vec{j}+\vec{k},\vec{n})$ e a norma unitária $\|\vec{n}\|=1$ são diretas, a ortogonalidade pode ser mostrada do produto interno

$\displaystyle\vec{i}\cdot\vec{n}$	$\displaystyle=\vec{i}\cdot\left(\frac{\sqrt{2}}{2}\vec{k}-\frac{\sqrt{2}}{2}% \vec{j}\right)$	(3.150)
	$\displaystyle=\frac{\sqrt{2}}{2}\vec{i}\cdot\vec{k}-\frac{\sqrt{2}}{2}\vec{i}% \cdot\vec{j}$	(3.151)
	$\displaystyle=0+0=0$	(3.152)

o que mostra que $\vec{i}\perp\vec{n}$ . Bem como, temos

$\displaystyle\left(\vec{j}+\vec{k}\right)\cdot\vec{n}$	$\displaystyle=\left(\vec{j}+\vec{k}\right)\cdot\left(\frac{\sqrt{2}}{2}\vec{k}% -\frac{\sqrt{2}}{2}\vec{j}\right)$	(3.153)
	$\displaystyle=\frac{\sqrt{2}}{2}\left(\vec{j}\cdot\vec{k}-\vec{j}\cdot\vec{j}+% \vec{k}\cdot\vec{k}-\vec{k}\cdot\vec{j}\right)$	(3.154)
	$\displaystyle=\frac{\sqrt{2}}{2}(0-1+1-0)=0,$	(3.155)

donde concluímos que $(\vec{j}+\vec{k})\perp\vec{n}$ . Isso mostra que

\vec{n}=\frac{\sqrt{2}}{2}\vec{k}-\frac{\sqrt{2}}{2}\vec{j}

(3.156)

e, portanto, de (3.147)

$\displaystyle\vec{i}\times(\vec{j}+\vec{k})$	$\displaystyle=\sqrt{2}\vec{n}$	(3.157)
	$\displaystyle=\sqrt{2}\left(\frac{\sqrt{2}}{2}\vec{k}-\frac{\sqrt{2}}{2}\vec{j% }\right)$	(3.158)
	$\displaystyle=\vec{k}-\vec{j}$	(3.159)
	$\displaystyle=\vec{i}\times\vec{j}+\vec{i}\times\vec{k}.$	(3.160)

Proposição 3.4.1.

(Distributividade para Vetores Canônicos.) Se $\vec{u}$ , $\vec{v}$ e $\vec{w}$ são vetores da base canônica¹⁶¹⁶endnote: ¹⁶ $\vec{i}$ , $\vec{j}$ ou $\vec{k}$ ., então vale a distributividade do produto vetorial

\vec{u}\times(\vec{v}+\vec{w})=\vec{u}\times\vec{v}+\vec{u}\times\vec{w}.

(3.161)

Demonstração.

Consulte o E.3.4.5. ∎

3.4.3 Associatividade por Escalar

Uma das propriedades fundamentais do produto vetorial é a associatividade com a multiplicação por escalar

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}(\alpha\vec{u}% )\times\vec{v}=\alpha\vec{u}\times\vec{v}.

(3.162)

Para mostrarmos isso, vamos precisar do seguinte resultado.

Mudança do Sentido

No produto vetores $\vec{u}\times\vec{v}$ , ao mudarmos o sentido de apenas um dos vetores, obtemos a seguinte relação

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}(-\vec{u})% \times\vec{v}=-(\vec{u}\times\vec{v})=\vec{u}\times(-\vec{v}).

(3.163)

De fato, assumindo que o ângulo $\theta$ e o vetor unitário $\vec{n}$ são tais que

\vec{u}\times\vec{v}=\|\vec{u}\|\|\vec{v}\|\operatorname{sen}(\theta)\vec{n},

(3.164)

temos

$\displaystyle(-\vec{u})\times\vec{v}$	$\displaystyle=\\|-\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\theta)(-\vec{n})$	(3.165)
	$\displaystyle=\|-1\|\\|\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\theta)(-\vec{n})$	(3.166)
	$\displaystyle=-\\|\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\theta)\vec{n}.$	(3.167)

E, de forma análoga, segue que $\vec{u}\times(-\vec{v})=-\vec{u}\times\vec{v}$ (consulte o E.3.4.11).

Associatividade com Multiplicação por Escalar

Agora, temos tudo para mostrar a associatividade

(\alpha\vec{u})\times\vec{v}=\alpha(\vec{u}\times\vec{v}).

(3.168)

De fato, assumindo $\alpha>0$ , o ângulo $\theta$ e o vetor normal unitário $\vec{n}$ tais que

\vec{u}\times\vec{v}=\|\vec{u}\|\|\vec{v}\|\operatorname{sen}(\theta)\vec{n},

(3.169)

temos que¹⁷¹⁷endnote: ¹⁷Observamos que $\vec{u}$ também é vetor normal unitário aos vetores $\alpha\vec{u}$ e $\vec{v}$ .

$\displaystyle(\alpha\vec{u})\times\vec{v}$	$\displaystyle=\\|\alpha\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\theta)\vec{n}$	(3.170)
	$\displaystyle=\|\alpha\|\\|\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\theta)\vec{n}$	(3.171)
	$\displaystyle=\alpha\\|\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\theta)\vec{n}$	(3.172)
	$\displaystyle=\alpha(\vec{u}\times\vec{v}).$	(3.173)

No caso de $\alpha<0$ , o resultado da propriedade da mudança do sentido (3.163), i.e.

$\displaystyle(\alpha\vec{u})\times\vec{v}$	$\displaystyle=-(-\alpha\vec{u})\times\vec{v}$	(3.174)
	$\displaystyle=-(-\alpha)(\vec{u}\times\vec{v})$	(3.175)
	$\displaystyle=\alpha(\vec{u}\times\vec{v}).$	(3.176)

Por raciocínio análogo, segue também que

\vec{u}\times(\alpha\vec{v})=\alpha(\vec{u}\times\vec{v})

(3.177)

para qualquer escalar $\alpha$ (consulte o E.3.4.12).

3.4.4 Produto Vetorial por Coordenadas

Usando as propriedades que estudamos até aqui, vamos mostrar que dados $\vec{u}=(u_{1},u_{2},u_{3})$ e $\vec{v}=(v_{1},v_{2},v_{3})$ em uma base ortonormal positiva, então

\vec{u}\times\vec{v}=\begin{vmatrix}u_{2}&u_{3}\\ v_{2}&v_{3}\end{vmatrix}\vec{i}-\begin{vmatrix}u_{1}&u_{3}\\ v_{1}&v_{3}\end{vmatrix}\vec{j}+\begin{vmatrix}u_{1}&u_{2}\\ v_{1}&v_{2}\end{vmatrix}\vec{k}

(3.178)

ou, mnemonicamente,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\vec{u}\times% \vec{v}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\ u_{1}&u_{2}&u_{3}\\ v_{1}&v_{2}&v_{3}\end{vmatrix}.

(3.179)

De fato, das propriedades da distributividade e da associatividade estudadas, temos

$\displaystyle\vec{u}\times\vec{v}$	$\displaystyle=(u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k})$	(3.180)
	$\displaystyle\quad\times(v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k})$	(3.181)
	$\displaystyle=(u_{2}v_{3}-u_{3}v_{2})\vec{i}$	(3.182)
	$\displaystyle\quad+(u_{3}v_{1}-u_{1}v_{3})\vec{j}$	(3.183)
	$\displaystyle\quad+(u_{1}v_{2}-u_{2}v_{1})\vec{k}$	(3.184)
	$\displaystyle=\begin{vmatrix}u_{2}&u_{3}\\ v_{2}&v_{3}\end{vmatrix}\vec{i}$	(3.187)
	$\displaystyle\quad-\begin{vmatrix}u_{1}&u_{3}\\ v_{1}&v_{3}\end{vmatrix}\vec{j}$	(3.190)
	$\displaystyle\quad+\begin{vmatrix}u_{1}&u_{2}\\ v_{1}&v_{2}\end{vmatrix}\vec{k}.$	(3.193)

Temos, portanto, mostrado (3.179).

Exemplo 3.4.1.

Dados os vetores $\vec{u}=(1,-2,1)$ e $\vec{v}=(0,2,-1)$ , temos

$\displaystyle\vec{u}\times\vec{v}$	$\displaystyle=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\ u_{1}&u_{2}&u_{3}\\ v_{1}&v_{2}&v_{3}\end{vmatrix}$	(3.197)
	$\displaystyle=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\ 1&-2&1\\ 0&2&-1\end{vmatrix}$	(3.201)
	$\displaystyle=0\vec{i}+\vec{j}+2\vec{k}$	(3.202)
	$\displaystyle=(0,1,2).$	(3.203)

3.4.5 Exercícios Resolvidos

ER 3.4.1.

Calcule $\vec{x}$ tal que $(0,2,-1)\times\vec{x}=(-3,-1,-2)$ .

Solução.

Denotando $\vec{x}=(x_{1},x_{2},x_{3})$ , temos

	$\displaystyle(0,2,-1)\times\vec{x}=(-3,-1,-2)$		(3.204)
	$\displaystyle\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\ 0&2&-1\\ x_{1}&x_{2}&x_{3}\end{vmatrix}=(-3,-1,-2)$		(3.208)
	$\displaystyle(x_{2}+2x_{3})\vec{i}-x_{1}\vec{j}-2x_{1}\vec{k}=$		(3.209)
	$\displaystyle-3\vec{i}-\vec{j}-2\vec{k}$		(3.210)

Segue que

	$\displaystyle x_{2}+2x_{3}$	$\displaystyle=-3$
	$\displaystyle-x_{1}$	$\displaystyle=-1$
	$\displaystyle-2x_{1}$	$\displaystyle=-2$

Logo, $x_{1}=1$ , $x_{2}=-3-2x_{3}$ e $x_{3}$ é arbitrário. Concluímos que $\vec{x}=(1,-3-2x_{3},x_{3})$ com $x_{3}\in\mathbb{R}$ .

ER 3.4.2.

Determine a área do paralelogramo determinado pelos vetores $\vec{u}=(-1,2,3)$ e $\vec{v}=(1,-2,1)$ .

Solução.

Tomando representações $\vec{u}=\overrightarrow{OA}$ e $\vec{v}=\overrightarrow{OC}$ , temos que $\vec{u}$ e $\vec{v}$ determinam um paralelogramo $O A B C$ , onde $B$ é tal que $\vec{u}+\vec{v}=\overrightarrow{OB}$ ¹⁸¹⁸endnote: ¹⁸Consulte a regra do paralelogramo na Subseção 1.3.3.. Da definição do produto vetorial, temos que

\|\vec{u}\times\vec{v}\|=\|\vec{u}\|\|\vec{v}\|\operatorname{sen}\theta,

(3.211)

o que é igual a área do paralelogramo $O A B C$ , onde $\theta$ é o ângulo entre os vetores $\vec{u}$ e $\vec{v}$ . Logo, a área do paralelogramo é

	$\displaystyle\\|\vec{u}\times\vec{v}\\|=\left\|\begin{vmatrix}\vec{i}&\vec{j}&% \vec{k}\\ -1&2&3\\ 1&-2&1\end{vmatrix}\right\|$		(3.215)
	$\displaystyle\\|\vec{u}\times\vec{v}\\|=\\|(8,4,0)\\|$		(3.216)
	$\displaystyle\\|\vec{u}\times\vec{v}\\|=4\sqrt{5}.$		(3.217)

3.4.6 Exercícios

E. 3.4.1.

A partir da definição do produto vetorial (3.136), calcule

a)

$\vec{i}\times\vec{j}$
b)

$\vec{j}\times\vec{k}$
c)

$\vec{k}\times\vec{i}$

Resposta.

a) $\vec{k}$ ; b) $\vec{i}$ ; c) $\vec{j}$

E. 3.4.2.

Repita o E.3.4.1, calculando cada item a partir do cálculo do produto vetorial por coordenadas (3.179).

Resposta.

a) $\vec{k}$ ; b) $\vec{i}$ ; c) $\vec{j}$

E. 3.4.3.

A partir da definição do produto vetorial (3.136), calcule

a)

$\vec{j}\times\vec{i}$
b)

$\vec{k}\times\vec{j}$
c)

$\vec{i}\times\vec{k}$

Resposta.

a) $-\vec{k}$ ; b) $-\vec{i}$ ; c) $-\vec{j}$

E. 3.4.4.

Repita o E.3.4.3, calculando cada item a partir do cálculo do produto vetorial por coordenadas (3.179).

Resposta.

a) $-\vec{k}$ ; b) $-\vec{i}$ ; c) $-\vec{j}$

E. 3.4.5.

A partir da definição do produto vetorial (3.136), mostre que

a)

$\vec{i}\times(\vec{i}+\vec{j})=\vec{k}$
b)

$\vec{j}\times(\vec{j}+\vec{k})=\vec{i}$
c)

$\vec{j}\times(\vec{i}+\vec{k})=-\vec{k}+\vec{i}$
d)

$\vec{k}\times(\vec{i}+\vec{j})=\vec{j}-\vec{i}$
e)

$\vec{k}\times(\vec{i}+\vec{k})=\vec{j}$
f)

$\vec{k}\times(\vec{j}+\vec{k})=-\vec{i}$

Resposta.

Dica: consulte a demonstração da (3.145).

E. 3.4.6.

Sejam $\vec{u}=(2,-3,1)$ e $\vec{v}=(1,-2,-1)$ . Calcule:

a)

$\vec{u}\times\vec{v}$ .
b)

$\vec{v}\times\vec{u}$ .
c)

$\vec{v}\times(2\vec{u})$ .

Resposta.

a) $(5,3,-1)$ ; b) $(-5,-3,1)$ ; c) $(-10,-6,2)$

E. 3.4.7.

Sejam $\vec{u}$ e $\vec{v}$ tais que $\vec{u}\times\vec{v}=(2,-1,0)$ . Forneça $\vec{v}\times\vec{u}$ . Justifique sua resposta.

Resposta.

$(-2,1,0)$

E. 3.4.8.

Seja $\vec{u}$ um vetor qualquer. Calcule $\vec{u}\times\vec{u}$ .

Resposta.

$0$

E. 3.4.9.

Sejam $\vec{u}$ e $\vec{v}$ tais que $(2\vec{u})\times\vec{v}=(2,-1,0)$ . Forneça $\vec{v}\times\vec{u}$ . Justifique sua resposta.

Resposta.

$(-1,1/2,0)$

E. 3.4.10.

Calcule $\vec{x}$ tal que $\vec{x}\times(2,-2,3)=(11,8,-2)$ .

Resposta.

$\left(\frac{2}{3}x_{3}-\frac{8}{3},-\frac{2}{3}x_{3}+\frac{11}{3},x_{3}\right)% ,x_{3}\in\mathbb{R}$

E. 3.4.11.

A partir da definição de produto vetorial (3.136), mostre que

\vec{u}\times(-\vec{v})=-\vec{u}\times\vec{v}.

(3.218)

Resposta.

Dica: estude a Subseção 3.4.3.

E. 3.4.12.

Mostre que vale a seguinte associatividade com multiplicação por escalar

\vec{u}\times(\alpha\vec{v})=\alpha(\vec{u}\times\vec{v}),

(3.219)

para quaisquer vetores $\vec{u}$ , $\vec{v}$ e escalar $\alpha$ .

Resposta.

Dica: estude a Subseção 3.4.3.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |

	$\displaystyle\\|\vec{u}\\|h$	$\displaystyle=\\|\vec{u}\\|\\|\vec{v}\\|\operatorname{sen}(\alpha)$		(3.137)
		$\displaystyle=\\|\vec{u}\times\vec{v}\\|.$		(3.138)

$\displaystyle\vec{i}\times\vec{j}$	$\displaystyle:=\\|\vec{i}\\|\\|\vec{j}\\|\operatorname{sen}(\alpha)\vec{n}$	(3.139)
	$\displaystyle=1\cdot 1\cdot\operatorname{sen}\left(\frac{\pi}{2}\right)\vec{k}$	(3.140)
	$\displaystyle=\vec{k}.$	(3.141)

$\displaystyle\vec{j}\times\vec{i}$	$\displaystyle:=\\|\vec{j}\\|\\|\vec{i}\\|\operatorname{sen}(\theta)\vec{n}$	(3.142)
	$\displaystyle=1\cdot 1\cdot\operatorname{sen}\left(\frac{\pi}{2}\right)(-\vec{% k})$	(3.143)
	$\displaystyle=-\vec{k}.$	(3.144)