Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

6 Equações Diferenciais Parciais 6.2 Equação do Calor Referências

6.3 Equação da Onda

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Consideramos a equação da onda com condições iniciais dadas e condições de contorno de Dirichlet homogêneas

	$\displaystyle u_{tt}-\alpha u_{xx}=0,\leavevmode\nobreak\ 0<t\leq t_{f},% \leavevmode\nobreak\ a<x<b,$		(6.39a)
	$\displaystyle u(0,x)=f(x),\leavevmode\nobreak\ a\leq x\leq b,$		(6.39b)
	$\displaystyle u_{t}(0,x)=g(x),\leavevmode\nobreak\ a\leq x\leq b,$		(6.39c)
	$\displaystyle u(t,a)=u(t,b)=0,\leavevmode\nobreak\ 0\leq t\leq t_{f},$		(6.39d)

onde $u=u(t,x)$ é a incógnita com $f$ , $g$ e $\alpha>0$ dadas.

Para a aplicação do Método das Diferenças Finitas (MDF), assumimos as discretizações: no tempo, $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}t^{(k)}=kh_{t}$ , $j=0,1,\dotsc,n_{t}$ , $h_{t}=t_{f}/n_{t}$ ; no espaço $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x_{i}=a+(i-1)h% _{x}$ , $i=1,2,\dotsc,n_{x}+1$ , $h_{x}=(b-a)/n_{x}$ . Então, assumindo a notação $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}u^{(k)}_{i}% \approx u\left(t^{(k)},x_{i}\right)$ usando a fórmula de diferenças finitas central $D^{2}_{0,h^{2}}$ , obtemos a seguinte forma discreta da equação Eq. (6.39a)

		$\displaystyle\frac{u^{(k-1)}_{i}-2u^{(k)}_{i}+\color[rgb]{0,0,1}\definecolor[% named]{pgfstrokecolor}{rgb}{0,0,1}\pgfsys@color@rgb@stroke{0}{0}{1}% \pgfsys@color@rgb@fill{0}{0}{1}u^{(k+1)}_{i}}{h_{t}^{2}}$		(6.40)
		$\displaystyle\quad-\alpha\frac{u^{(k)}_{i}-2u^{(k)}_{i}+u^{(k)}_{i+1}}{h_{x}^{% 2}}=0,$		(6.40)

para $i=2,3,\dotsc,n_{x}$ , $j=1,2,\dotsc,n_{t}-1$ . Denotando $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\lambda:=% \alpha h_{t}^{2}/h_{x}^{2}$ , rearranjando os termos e aplicando as condições de contorno, obtemos

	$\displaystyle u^{(k+1)}_{2}=2\left(1-\lambda\right)u^{(k)}_{2}+\lambda u^{(k)}% _{3}-u^{(k-1)}_{2},$		(6.41a)
	$\displaystyle u^{(k+1)}_{i}=\lambda u^{(k)}_{i}+2(1-\lambda)u^{(k)}_{i}+% \lambda u^{(k)}_{i+1}-u^{(k-1)}_{i},$		(6.41b)
	$\displaystyle u^{(k+1)}_{n_{x}}=\lambda u^{(k)}_{n_{x}-1}+2(1-\lambda)u^{(k)}_% {n_{x}}-u^{(k-1)}_{n_{x}},$		(6.41c)

para $i=2,3,\dotsc,n_{x}$ , $j=1,2,\dotsc,n_{t}-1$ . Ou, equivalentemente, na forma matricial

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\tilde{% \boldsymbol{u}}^{(k+1)}=A\tilde{\boldsymbol{u}}^{(k)}-\tilde{\boldsymbol{u}}^{% (k-1)},

(6.42)

para $k=1,2,\dotsc,n_{t}-1$ , onde $\tilde{\boldsymbol{u}}^{(k)}=\left(u^{(k)}_{i}\right)_{i=2}^{n_{x}}$ e $A=[a_{i,j}]_{i,j=1}^{n_{x}-1,n_{x}-1}$ é a matriz tridiagonal de elementos

a_{i,j}=\left\{\begin{array}[]{ll}a_{i,i-1}=\lambda&,1<i\leq n_{x}-1,\\ a_{i,i}=2(1-\lambda)&,1\leq i\leq n_{x}-1,\\ a_{i,i+1}=\lambda&,1\leq i<n_{x}-1.\\ \end{array}\right.

(6.43)

Para a inicialização, a Eq. (6.42) requer que conhecemos $\tilde{\boldsymbol{u}}^{(0)}$ e $\tilde{\boldsymbol{u}}^{(1)}$ . A primeira, vem diretamente da condição inicial Eq. (6.39b), i.e.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\tilde{% \boldsymbol{u}}^{(0)}=f\left(\tilde{\boldsymbol{x}}\right),

(6.44)

onde $\tilde{\boldsymbol{x}}=\left(x_{i}\right)_{i=2}^{n_{x}}$ . Agora, aplicando a fórmula de diferenças finitas progressiva $D_{+,h}$ , temos da condição inicial Eq. (6.39c)

\frac{\tilde{\boldsymbol{u}}^{(1)}-\tilde{\boldsymbol{u}}^{(0)}}{h_{t}}=g\left% (\tilde{\boldsymbol{x}}\right)

(6.45)

ou, equivalentemente,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\tilde{% \boldsymbol{u}}^{(1)}=\tilde{\boldsymbol{u}}^{(0)}+h_{t}g\left(\tilde{% \boldsymbol{x}}\right).

(6.46)

De tudo isso, temos que a solução numérica da equação da onda pode ser computada com a seguinte iteração

	$\displaystyle\tilde{\boldsymbol{u}}^{(0)}=f\left(\tilde{\boldsymbol{x}}\right),$		(6.47a)
	$\displaystyle\tilde{\boldsymbol{u}}^{(1)}=\tilde{\boldsymbol{u}}^{(0)}+h_{t}g% \left(\tilde{\boldsymbol{x}}\right),$		(6.47b)
	$\displaystyle\tilde{\boldsymbol{u}}^{(k+1)}=A\tilde{\boldsymbol{u}}^{(k)}-% \tilde{\boldsymbol{u}}^{(k-1)},$		(6.47c)

para $k=1,2,\dotsc,n_{t}-1$ , com $\boldsymbol{u}^{(k)}=\left(0,\tilde{\boldsymbol{u}},0\right)$ .

Observação 6.3.1.

(Condição de Estabilidade e Erro de Truncamento.) Pode-se mostrar a seguinte condição de estabilidade [3, p. 487]

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\alpha\frac{h_% {t}}{h_{x}}\leq 1.

(6.48)

Com isso e para $f$ e $g$ suficientemente suaves, o esquema numérica (6.3) tem erro de truncamento $O(h_{t}^{2}+h_{x}^{2})$ .

Exemplo 6.3.1.

Consideramos o seguinte problema

	$\displaystyle u_{tt}-u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 2,\leavevmode% \nobreak\ 0<x<1,$		(6.49a)
	$\displaystyle u(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.49b)
	$\displaystyle u_{t}(0,x)=\pi\operatorname{sen}(\pi x),\leavevmode\nobreak\ 0% \leq x\leq 1,$		(6.49c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 2.$		(6.49d)

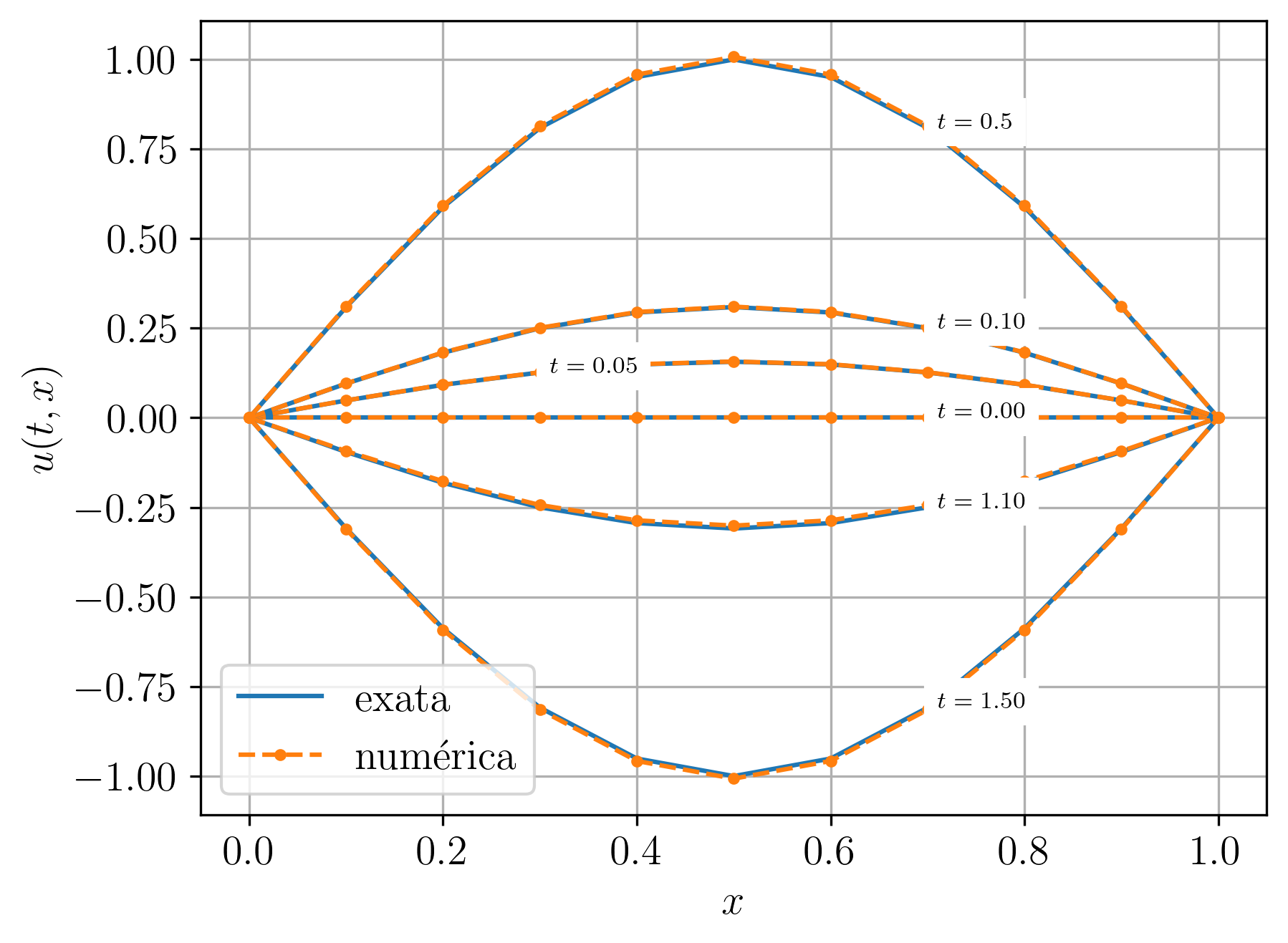
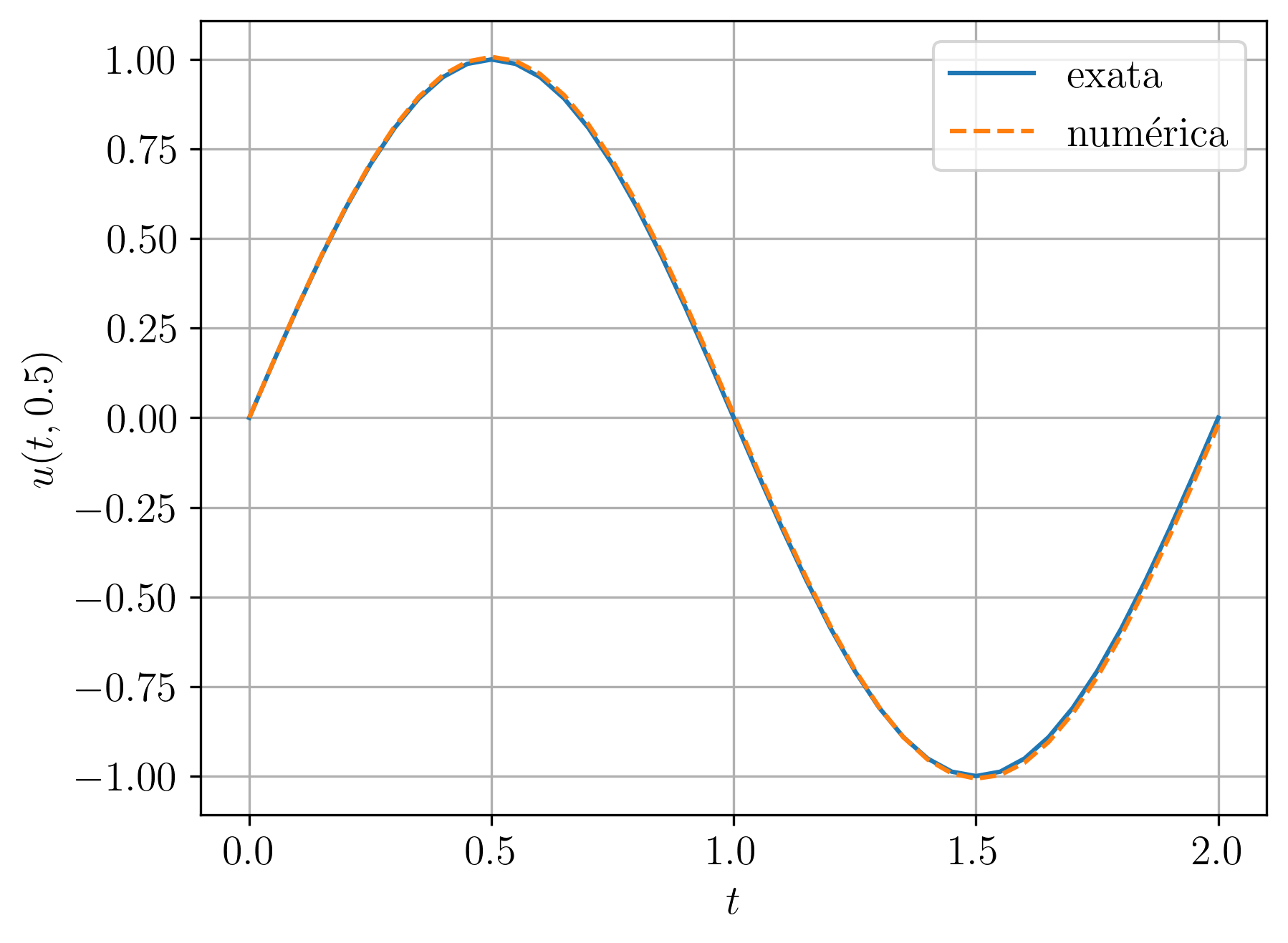
Sua solução exata é $u(t,x)=\operatorname{sen}(\pi t)\operatorname{sen}(\pi x)$ . A Figura 6.6 contém gráficos de comparação entra as soluções numérica e exata. Para a solução numérica, tomamos $n_{t}=40$ ( $h_{t}=0.05$ ) e $n_{x}=10$ ( $h_{x}=0.1$ ).

Refer to caption — Figura 6.6: Gráficos comparativos das soluções numérica e exata do problema de onda do Exemplo 6.3.1.

⬇

1import numpy as np

2from numpy import pi, sin, cos

4# params

5nt = 40

6ht = 2./nt

7tt = np.linspace(0., 2., nt+1)

9nx = 10

10hx = 1./nx

11xx = np.linspace(0., 1., nx+1)

13# c.i.s

14def f(x):

15 return np.zeros_like(x)

17def g(x):

18 return pi*sin(pi*x)

20# axiliares

21lbda = ht**2/hx**2

23A = np.zeros(((nx-1), (nx-1)))

24A[0,0] = 2*(1. - lbda)

25A[0,1] = lbda

26for i in range(1,nx-2):

27 A[i,i-1] = lbda

28 A[i,i] = 2*(1 - lbda)

29 A[i,i+1] = lbda

30A[nx-2,nx-3] = lbda

31A[nx-2,nx-2] = 2*(1 - lbda)

33# laço no tempo

34## c.i.s

35u0 = f(xx)

37u1 = u0.copy()

38u1[1:-1] = u0[1:-1] + ht*g(xx[1:-1])

40u = u1.copy()

41for k in range(1,nt):

43 print(f'{k+1}: t = {tt[k+1]:f}')

45 u[1:-1] = A@u1[1:-1] - u0[1:-1]

47 u0 = u1.copy()

48 u1 = u.copy()

6.3.1 Exercício

E. 6.3.1.

Considere o problema

	$\displaystyle u_{tt}-u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 1.5,\leavevmode% \nobreak\ 0<x<1,$		(6.50a)
	$\displaystyle u(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.50b)
	$\displaystyle u_{t}(0,x)=\pi\operatorname{sen}(\pi x),\leavevmode\nobreak\ 0% \leq x\leq 1,$		(6.50c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 1.5.$		(6.50d)

Sua solução exata é $u(t,x)=\operatorname{sen}(\pi t)\operatorname{sen}(\pi x)$ . Faça testes numéricos para determinar os passos $h_{t}$ e $h_{x}$ para os quais o esquema numérico (6.3) compute o valor de $u(1.5,0.5)$ com $5$ dígitos significativos corretos.

Resposta.

$h_{t}=2.5\mathrm{e}\!-3\!$ , $h_{x}=1.\mathrm{e}\!-2\!$

E. 6.3.2.

Considere o problema

	$\displaystyle u_{tt}-u_{xx}=e^{-t}(2+x-x^{2}),\leavevmode\nobreak\ 0<t\leq 1,% \leavevmode\nobreak\ 0<x<1,$		(6.51a)
	$\displaystyle u(0,x)=x-x^{2},\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.51b)
	$\displaystyle u_{t}(0,x)=x^{2}-x,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.51c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 1.$		(6.51d)

Sua solução exata é $u(t,x)=e^{-t}(x-x^{2})$ . Implemente um esquema numérico semelhante ao (6.3) para computar soluções numéricas desse problema.

E. 6.3.3.

Considere o problema

	$\displaystyle u_{tt}-u_{xx}=e^{-t}(2+x-x^{2}),\leavevmode\nobreak\ 0<t\leq 1,% \leavevmode\nobreak\ 0<x<1,$		(6.52a)
	$\displaystyle u(0,x)=x-x^{2},\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.52b)
	$\displaystyle u_{t}(0,x)=x^{2}-x,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.52c)
	$\displaystyle u_{x}(t,0)=e^{-t},\leavevmode\nobreak\ 0\leq t\leq 1,$		(6.52d)
	$\displaystyle u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 1.$		(6.52e)

Sua solução exata é $u(t,x)=e^{-t}(x-x^{2})$ . Implemente um esquema numérico semelhante ao (6.3) para computar soluções numéricas desse problema.

E. 6.3.4.

Considere o problema

	$\displaystyle u_{tt}-u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 2,\leavevmode% \nobreak\ 0<x<1,$		(6.53a)
	$\displaystyle u(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.53b)
	$\displaystyle u_{t}(0,x)=\pi\operatorname{sen}(\pi x),\leavevmode\nobreak\ 0% \leq x\leq 1,$		(6.53c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 2.$		(6.53d)

Sua solução exata é $u(t,x)=\operatorname{sen}(\pi t)\operatorname{sen}(\pi x)$ . Baseado em (6.3), desenvolva um novo esquema numérico substituindo o passo (6.47b) por um esquema numérico de mais alta ordem.

Resposta.

Dica: use, por exemplo, um método de R-K-2.

E. 6.3.5.

Considere o problema

	$\displaystyle u_{tt}-\alpha u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 1,% \leavevmode\nobreak\ 0<x<1,$		(6.54a)
	$\displaystyle u(0,x)=x(1-x),\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.54b)
	$\displaystyle u_{t}(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.54c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 2.$		(6.54d)

Use o esquema numérico (6.3) para fazer testes numéricos para $\alpha=1.,0.5,0.1,0.01$ . É necessário ajustar os parâmetros $h_{t}$ e $h_{x}$ ao variar o parâmetro $\alpha$ ? Justifique sua resposta.

Resposta.

Dica: consulte a Observação 6.3.1.

Notas

1 Para fixar notação, assumiremos $h>0$ ao longo deste capítulo.
2 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
3 Consulte [3, Cap. 7,Sec. 1.1], para uma abordagem mais geral.
4 Neste capítulo, $h$ é escolhido como a distância entre os nodos.
5 Thomas Simpson, 1710 - 1761, matemático britânico. Fonte: Wikipédia: Thomas Simpson.
6 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
7 Para a estimativa do erro de truncamento, consulte o Exercício 3.1.5.
8 Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.
9 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
10 Equações Diferenciais Ordinárias
11 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
12 Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.
13 Carl David Tolmé Runge, 1856 - 1927, matemático alemão. Fonte: Wikipédia: Carl Runge.
14 Martin Wilhelm Kutta, 1867 - 1944, matemático alemão. Fonte: Wikipédia: Martin Wilhelm Kutta.
15 Consulte (4.83) para mais detalhes sobre a expansão em polinômio de Taylor de $\Delta(t,y;h)$ .
16 Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.
17 Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.
18 Roger Cotes, 1682 - 1716, matemático inglês. Fonte: Wikipédia: Roger Cotes.
19 Consulte as Notas de Aula: Matemática Numérica II: Integração: Regras de Newton-Cotes.
20 Consulte o Exercício 4.5.6
21 Com erro de truncamento local de $O(h^{2})$ .
22 Por convenção, (5.2a)-(5.2c) é chamado de formulação forte do problema.
23 $u\in L^{2}([a,b])\Leftrightarrow\int_{a}^{b}|u|^{2}\,dx<\infty$ .
24 $H_{0}^{1}([a,b]):=\{u=u(x);\leavevmode\nobreak\ u,u^{\prime}\in L^{2}([a,b]),u% (a)=u(b)=0\}$ .
25 Por simplicidade, usando a regra do ponto médio para aproximar as integrais.
26 Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.
27 Carl Gustav Jakob Jacobi, 1804 - 1851, matemático alemão. Fonte: Wikipédia: Carl Gustav Jakob Jacobi.
28 Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.
29 Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace.
30 Carl Gottfried Neumann, 1832 - 1925, matemático alemão. Fonte: Wikipédia: Carl Neumann.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |