Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

5 Problema de Valor de Contorno 5.1 Método de Diferenças Finitas 5.3 Método de Volumes Finitos

5.2 Método de Elementos Finitos

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Consideramos o seguinte problema linear de valor de contorno (PVC)

	$\displaystyle-u^{\prime\prime}=f(x),\leavevmode\nobreak\ a<x<b,$		(5.33a)
	$\displaystyle u(a)=0,$		(5.33b)
	$\displaystyle u(b)=0.$		(5.33c)

onde a incógnita é $u=u(x)$ com dada fonte $f=f(x)$ .

A solução pelo Método de Elementos Finitos (FEM) de (5.2a)-(5.2c) surge da aproximação do problema em um espaço de dimensão finita de funções. São três passos fundamentais: 1. escrever a formulação fraca do problema²²²²endnote: ²²Por convenção, (5.2a)-(5.2c) é chamado de formulação forte do problema., 2. escrever a formulação de elementos finitos e 3. resolver o problema de elementos finitos.

1. Formulação Fraca

Para obter a formulação fraca do PVC (5.73)-(5.33c), multiplicamos (5.73) por uma arbitrária função teste $v=v(x)$

-u^{\prime\prime}v=fv

(5.34)

e integramos no domínio $a\leq x\leq b$ , i.e.

-\int_{a}^{b}u^{\prime\prime}v\,dx=\int_{a}^{b}fv\,dx.

(5.35)

Então, aplicando integração por partes no primeiro termo do lado esquerdo, obtemos

\int_{a}^{b}u^{\prime}v^{\prime}\,dx-\left[u^{\prime}v\right]_{x=a}^{b}=\int_{% a}^{b}fv\,dx.

(5.36)

Vamos denotar o produto interno em $L^{2}([a,b])$ ²³²³endnote: ²³ $u\in L^{2}([a,b])\Leftrightarrow\int_{a}^{b}|u|^{2}\,dx<\infty$ . por

(u,v)_{2}:=\int_{a}^{b}uv\,dx

(5.37)

e nos contornos

\langle u,v\rangle:=u(b)v(b)-u(a)v(a).

(5.38)

Com isso, definimos a formulação fraca como o seguinte problema: encontrar $u\in V:=H_{0}^{1}([a,b])$ ²⁴²⁴endnote: ²⁴ $H_{0}^{1}([a,b]):=\{u=u(x);\leavevmode\nobreak\ u,u^{\prime}\in L^{2}([a,b]),u% (a)=u(b)=0\}$ . tal que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}a(u,v)=l(v),% \leavevmode\nobreak\ \forall v\in V,

(5.39)

onde a forma bilinear é

a(u,v):=(u^{\prime},v^{\prime})_{2}

(5.40)

e a forma linear é

l(v):=(f,v)_{2}.

(5.41)

2. Formulação de Elementos Finitos

A formulação de elementos finitos do problema (5.73)-(5.33c) é obtida a partir de (5.39) pela substituição do espaço de funções $V$ por um espaço de dimensão finita $V_{h}$ . A ideia é que $V_{h}\to V$ , bem como a solução de elementos finitos $u_{h}\to u\in V$ quando $h\to 0$ .

Para construir o espaço de elementos finitos $V_{h}$ , vamos considerar elementos do tipo

	$\displaystyle P_{1}(I):=$	$\displaystyle\left\{v=v(x);v(x)=c_{0}+c_{1}x,\right.$		(5.42)
		$\displaystyle\qquad\qquad\qquad\left.x\in I,c_{0},c_{1}\in\mathbb{R}\right\},$		(5.42)

onde $I$ é um intervalo fechado.

Sobre o domínio, assumimos uma malha uniforme

M([a,b]):=\{x_{1},x_{2},\dotsc,x_{n+1}\}

(5.43)

com $h=(b-a)/n$ , $x_{i}=a+(i-1)h$ , $i=1,2,\dotsc,n+1$ . Nesta, definimos o espaço de funções

	$\displaystyle V_{h,0}$	$\displaystyle:=\left\{v=v(x);v\in C^{0}[a,b],v(a)=v(b)=0,\right.$		(5.44)
		$\displaystyle\left.\qquad\qquad\qquad v\|_{[x_{i},x_{i+1}]}\in P_{1}([x_{i},x_{% i+1}]),i=1,2,\dotsc,n\right\}.$		(5.44)

Pode-se mostrar que $V_{h}=\operatorname{span}\{\phi_{i}\}_{i=1}^{n-1}$ , com base nodal

\phi_{j}(x_{i})=\left\{\begin{array}[]{ll}1&,i=j,\\ 0&,i\neq j\end{array}\right.

(5.45)

para $i,j=2,\dotsc,n$ e $\phi_{1}(a)=0=\phi_{n}(b)$ . Podemos verificar que

\phi_{i}(x)=\left\{\begin{array}[]{ll}(x-x_{i-1})/h&,x\in[x_{i-1},x_{i}],\\ (x_{i+1}-x)/h&,x\in[x_{i},x_{i+1}],\\ 0&,\text{noutros casos}\end{array}\right.

(5.46)

Com isso, definimos a formulação de elementos finitos sendo o seguinte problema: encontrar $u_{h}\in V_{h,0}$ tal que

a(u_{h},v_{h})=l(v_{h}),\leavevmode\nobreak\ \forall v_{h}\in V_{h}.

(5.47)

Tendo em vista que $V_{h}=\operatorname{span}\{\phi_{i}\}_{i=1}^{n+1}$ , este é equivalente a

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}a(u_{h},\phi_{% j})=l(\phi_{j}),\leavevmode\nobreak\ \forall 1\leq j\leq n-1.

(5.48)

3. Resolução do Problema de Elementos Finitos

O problema de elementos finitos (5.48) consiste em um sistema linear $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}A\boldsymbol{u% }=\boldsymbol{b}$ . De fato, a solução $u_{h}\in V_{h,0}$ pode ser escrita como a seguinte combinação linear

u_{h}=\sum_{j=1}^{n-1}u_{j}\phi_{j}.

(5.49)

Logo, temos que

$\displaystyle a(u_{h},\phi_{i})$	$\displaystyle=\left(\sum_{j=1}^{n-1}u_{j}\phi_{j},\phi_{i}\right)_{2},$	(5.50a)
	$\displaystyle=\sum_{j=1}^{n-1}u_{j}(\phi_{j},\phi_{i})_{2},$	(5.50b)
	$\displaystyle=A\boldsymbol{u},$	(5.50c)

onde a matriz dos coeficientes é $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}A=\left[a_{i,j% }:=(\phi_{j},\phi_{i})\right]_{i,j=1}^{n-1}$ e o vetor das incógnitas é $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\boldsymbol{u}% =(u_{j})_{j=1}^{n-1}$ . Doutro lado, temos

l(\phi_{i})=(f,\phi_{i})_{2},

(5.51)

o que nos fornece o vetor dos termos constantes $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\boldsymbol{b}% =\left(b_{i}:=(f,\phi_{i})_{2}\right)_{i=1}^{n-1}$ .

O cálculo dos elementos de $A$ fornece

$\displaystyle a_{i,i}$	$\displaystyle=(\phi^{\prime}_{i},\phi^{\prime}_{i})_{2}$	(5.52a)
	$\displaystyle=\int_{a}^{b}\left(\phi^{\prime}_{i}\right)^{2}\,dx$	(5.52b)
	$\displaystyle=\int_{x_{i-1}}^{x_{i+1}}(\phi^{\prime}_{i})^{2}\,dx$	(5.52c)
	$\displaystyle=\int_{x_{i-1}}^{x_{i}}\left[\left(\frac{x-x_{i-1}}{h}\right)^{% \prime}\right]^{2}\,dx$	(5.52d)
	$\displaystyle+\int_{x_{i}}^{x_{i+1}}\left[\left(\frac{x_{i+1}-x}{h}\right)^{% \prime}\right]^{2}\,dx$	(5.52e)
	$\displaystyle=\frac{2}{h},\leavevmode\nobreak\ i=1,2,\dotsc,n-1,$	(5.52f)

$\displaystyle a_{i,i+1}$	$\displaystyle=(\phi^{\prime}_{i+1},\phi^{\prime}_{i})_{2}$	(5.53a)
	$\displaystyle=\int_{a}^{b}\phi^{\prime}_{i+1}\phi^{\prime}_{i}\,dx$	(5.53b)
	$\displaystyle=\int_{x_{i}}^{x_{i+1}}\left(\frac{x_{i+1}-x}{h}\right)^{\prime}% \left(\frac{x-x_{i+1}}{h}\right)^{\prime}\,dx$	(5.53c)
	$\displaystyle=-\frac{1}{h},\leavevmode\nobreak\ i=1,2,\dotsc,n-2,$	(5.53d)

$\displaystyle a_{i-1,i}$	$\displaystyle=(\phi^{\prime}_{i-1},\phi^{\prime}_{i})_{2}$	(5.54a)
	$\displaystyle=\int_{a}^{b}\phi_{i-1}\phi_{i}\,dx$	(5.54b)
	$\displaystyle=\int_{x_{i-1}}^{x_{i}}\left(\frac{x_{i}-x}{h}\right)^{\prime}% \left(\frac{x-x_{i}}{h}\right)^{\prime}\,dx$	(5.54c)
	$\displaystyle=-\frac{1}{h},\leavevmode\nobreak\ i=2,\dotsc,n-1,$	(5.54d)

observando que, noutros casos, $a_{i,j}=0$ .

Um cálculo aproximado dos elementos de $\boldsymbol{b}$ fornece²⁵²⁵endnote: ²⁵Por simplicidade, usando a regra do ponto médio para aproximar as integrais.

$\displaystyle b_{i}$	$\displaystyle=(f,\phi_{i})_{2}$	(5.55a)
	$\displaystyle=\int_{a}^{b}f(x)\phi_{i}(x)\,dx$	(5.55b)
	$\displaystyle=\int_{x_{i-1}}^{x_{i}}f(x)\frac{(x-x_{i-1})}{h}\,dx$	(5.55c)
	$\displaystyle+\int_{x_{i}}^{x_{i+1}}f(x)\frac{(x_{i+1}-x)}{h}\,dx$	(5.55d)
	$\displaystyle\approx\frac{h}{2}f(x_{i-1/2})+\frac{h}{2}f(x_{i+1/2}).$	(5.55e)

Exemplo 5.2.1.

Consideramos o seguinte PVC

	$\displaystyle-u^{\prime\prime}=\pi^{2}\operatorname{sen}(\pi x),\leavevmode% \nobreak\ 0<x<1,$		(5.56)
	$\displaystyle u(0)=0,$		(5.57)
	$\displaystyle u(1)=0.$		(5.58)

A solução analítica deste problema é $u(x)=\operatorname{sen}(\pi x)$ .

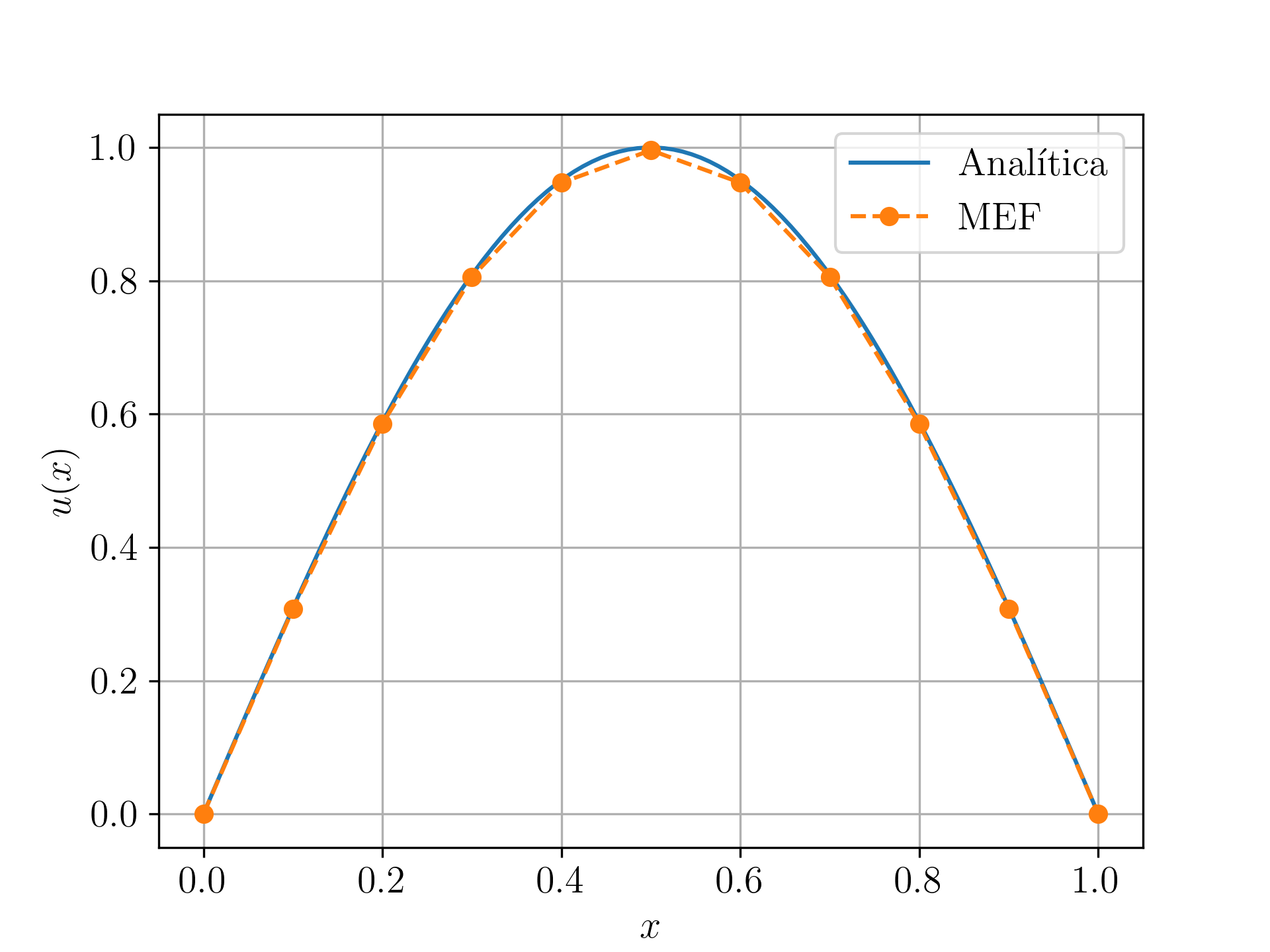
Refer to caption — Figura 5.2: Resultado referente ao Exemplo 5.2.1.

Resolvendo este sistema com $h=10^{-1}$ obtemos a solução numérica apresentada na Figura 5.2.

Código 17: pvc_mef.py

⬇

1import numpy as np

3# malha

4n = 10

5h = 1./n

6xx = np.linspace(0., 1., n+1)

8# fonte

9def f(x):

10 return np.pi**2*np.sin(np.pi*x)

12# prob discreto

13A = np.zeros((n-1, n-1))

14b = np.empty(n-1)

16# c.c. x = 0.

17A[0,0] = 2./h

18A[0,1] = -1./h

19b[0] = h/2 * (f(xx[1]-0.5*h) + f(xx[1]+0.5*h))

21# pts internos

22for i in range(1,n-2):

23 A[i,i-1] = -1./h

24 A[i,i] = 2./h

25 A[i,i+1] = -1./h

26 b[i] = h/2 * (f(xx[i+1]-0.5*h) + f(xx[i+1]+0.5*h))

28# c.c. x = 1.

29A[n-2,n-3] = -1./h

30A[n-2,n-2] = 2./h

31b[n-2] = h/2 * (f(xx[n-1]-0.5*h) + f(xx[n-1]+0.5*h))

33# resol

34u = npla.solve(A, b)

35## c.c. (dirichlet)

36u = np.concatenate(([0.],u,[0.]))

5.2.1 Exercícios

E. 5.2.1.

Considere o PVC

	$\displaystyle-u^{\prime\prime}=\pi^{2}\cos(\pi x),\leavevmode\nobreak\ 0<x<1,$		(5.59)
	$\displaystyle u(0)=1,$		(5.60)
	$\displaystyle u(1)=-1.$		(5.61)

A solução analítica deste problema é $u(x)=\cos(\pi x)$ . Use o MEF para computar aproximações numéricas $\tilde{\boldsymbol{u}}_{h}$ com tamanhos de malha $h=10^{-1},10^{-2},10^{-3},10^{-4}$ e verifique o erro absoluto $\varepsilon_{\text{abs}}:=\|\tilde{\boldsymbol{u}}_{h}-\boldsymbol{u}\|$ .

E. 5.2.2.

Considere o PVC

	$\displaystyle-u^{\prime\prime}=2,\leavevmode\nobreak\ -1<x<1,$		(5.62)
	$\displaystyle u(-1)=0,$		(5.63)
	$\displaystyle u(1)=0.$		(5.64)

A solução analítica deste problema é $u(x)=1-x^{2}$ . Use o MEF com $n=20$ subintervalos na malha e verifique o erro absoluto $\varepsilon_{\text{abs}}:=\|\tilde{\boldsymbol{u}}_{h}-\boldsymbol{u}\|$ . Por que o erro está próximo precisão de máquina? Justifique sua resposta.

E. 5.2.3.

Considere o seguinte PVC

	$\displaystyle-u^{\prime\prime}+u^{\prime}=f(x),\leavevmode\nobreak\ -1<x<1,$		(5.65a)
	$\displaystyle u(-1)=0,$		(5.65b)
	$\displaystyle u^{\prime}(1)=0,$		(5.65c)

onde

f(x)=\left\{\begin{array}[]{ll}1&,x\leq 0\\ 0&,x>0\end{array}\right.

(5.66)

Use uma aproximação adequada pelo MEF para obter o valor aproximado de $u(0)$ com precisão de $2$ dígitos significativos.

Resposta.

$7,2\mathrm{e}\!-\!1$

E. 5.2.4.

Considere o PVC

	$\displaystyle-u^{\prime\prime}=\pi^{2}\cos(\pi x),\leavevmode\nobreak\ 0<x<1,$		(5.67)
	$\displaystyle u(0)=1,$		(5.68)
	$\displaystyle u^{\prime}(1)=0.$		(5.69)

A solução analítica deste problema é $u(x)=\cos(\pi x)$ . Aplique o MEF para computar uma aproximação numérica com erro absoluto de no máximo $10^{-3}$ na norma $L^{2}$ .

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |