Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

5 Problema de Valor de Contorno 5.3 Método de Volumes Finitos 6 Equações Diferenciais Parciais

5.4 Problemas Não-Lineares

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Vamos estudar a resolução de Problemas Não-Lineares de Valores de Contorno da forma

	$\displaystyle u_{xx}=f\left(x,u,u_{x}\right),\leavevmode\nobreak\ a\leq x\leq b,$		(5.99a)
	$\displaystyle u(a)=u_{a},$		(5.99b)
	$\displaystyle u(b)=u_{b},$		(5.99c)

onde $f=f(x,u,u_{x})$ é uma função não linear para $u$ ou $u_{x}$ .

Empregando o Método de Diferenças Finitas (MDF), começamos assumindo uma malha uniforme de $n$ -subintervalos com nodos $x_{i}=a+(i-1)h$ , tamanho de malha $h=(b-a)/n$ , $i=1,2,\dotsc,n+1$ . Denotando $u_{i}\approx u(x_{i})$ e aplicando fórmulas de diferenças finitas centrais para $u_{xx}$ e $u_{x}$ , a Eq. (5.99a) fornece

		$\displaystyle\frac{1}{h^{2}}u_{i-1}-\frac{2}{h^{2}}u_{i}\frac{1}{h^{2}}u_{i+1}=$		(5.100)
		$\displaystyle\quad\quad f\left(x_{i},u_{i},\frac{1}{2h}u_{i+1}-\frac{1}{2h}u_{% i-1}\right),$		(5.100)

para $i=2,3,\dotsc,n$ . As condições de contorno Eqs. (5.99b)-(5.99c), fornecem as equações de fechamento

	$\displaystyle u_{1}=u_{a},$		(5.101a)
	$\displaystyle u_{n+1}=u_{b}.$		(5.101b)

Com isso, temos que o problema discreto associado consiste em: encontrar $\boldsymbol{u}=(u_{i})_{i=1}^{n+1}$ solução do seguinte sistema de equações não-lineares

	$\displaystyle u_{1}-u_{a}=0,$		(5.102a)
	$\displaystyle-\frac{1}{h^{2}}u_{i-1}+\frac{2}{h^{2}}u_{i}-\frac{1}{h^{2}}u_{i+1}$
	$\displaystyle\quad\quad\quad+f\left(x_{i},u_{i},\frac{1}{2h}u_{i+1}-\frac{1}{2% h}u_{i-1}\right)=0,$		(5.102b)
	$\displaystyle u_{n+1}-u_{b}=0.$		(5.102c)

A resolução do problema discreto (5.4) pode ser feito com o Método de Newton²⁶²⁶endnote: ²⁶Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.. Para tando, observamos que o sistema tem a forma vetorial

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}F(\boldsymbol{% u})=\boldsymbol{0},

(5.103)

onde $F(\boldsymbol{u})=\left(f_{i}(\boldsymbol{u})\right)_{i=1}^{(n+1)}$ é a função vetorial de componentes

$\displaystyle f_{1}(\boldsymbol{u})$	$\displaystyle=u_{1}-u_{a},$	(5.104a)
$\displaystyle f_{i}(\boldsymbol{u})$	$\displaystyle=-\frac{1}{h^{2}}u_{i-1}+\frac{2}{h^{2}}u_{i}-\frac{1}{h^{2}}u_{i% +1}$
	$\displaystyle\quad\quad+f\left(x_{i},u_{i},\frac{1}{2h}u_{i+1}-\frac{1}{2h}u_{% i-1}\right),$	(5.104b)
$\displaystyle f_{n+1}(\boldsymbol{u})$	$\displaystyle=u_{n+1}-u_{b},$	(5.104c)

com $i=2,3,\dotsc,n$ . A iteração do Método de Newton consiste em

	$\displaystyle\boldsymbol{u}^{(0)}=\text{aprox. inicial},$		(5.105a)
	$\displaystyle\boldsymbol{u}^{(k+1)}=\boldsymbol{u}^{(k)}+\boldsymbol{\delta}^{% (k)},$		(5.105b)

onde $\boldsymbol{\delta}^{(k)}$ é a atualização de Newton computada por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}J_{F}\left(% \boldsymbol{u}^{(k)}\right)\boldsymbol{\delta}^{(k)}=-F\left(\boldsymbol{u}^{(% k)}\right),

(5.106)

para $k=0,1,2,\ldots$ até que um critério de parada seja satisfeito. A matriz jacobiana²⁷²⁷endnote: ²⁷Carl Gustav Jakob Jacobi, 1804 - 1851, matemático alemão. Fonte: Wikipédia: Carl Gustav Jakob Jacobi. é denotada por $J_{F}\left(\boldsymbol{u}^{(k)}\right)=[\jmath_{i,j}]_{i,j=1}^{n+1,n+1}$ e tem elementos não nulos

\jmath_{1,1}=1,

(5.107)

	$\displaystyle\jmath_{i,i-1}=-\frac{1}{h^{2}}-\frac{1}{2h}f_{u_{x}}\left(x_{i},% u_{i},\frac{1}{2h}u_{i+1}-\frac{1}{2h}u_{i-1}\right),$		(5.108a)
	$\displaystyle\jmath_{i,i}=\frac{2}{h^{2}}+f_{u}\left(x_{i},u_{i},\frac{1}{2h}u% _{i+1}-\frac{1}{2h}u_{i-1}\right),$		(5.108b)
	$\displaystyle\jmath_{i,i+1}=-\frac{1}{h^{2}}+\frac{1}{2h}f_{u_{x}}\left(x_{i},% u_{i},\frac{1}{2h}u_{i+1}-\frac{1}{2h}u_{i-1}\right),$		(5.108c)

para $i=2,3,\dotsc,n$ e

\jmath_{n+1,n+1}=1.

(5.109)

Exemplo 5.4.1.

Vamos considerar o seguinte PVC

	$\displaystyle uu_{x}-u_{xx}=\pi\operatorname{sen}(\pi x)\left[\pi+\cos(\pi x)% \right],\leavevmode\nobreak\ 0<x<1,$		(5.110a)
	$\displaystyle u(0)=u(1)=0.$		(5.110b)

Rearranjando os termos, podemos escrevê-lo na forma da Eq. (5.4), com $u_{a}=u_{b}=0$ e

f(x,u,u_{x})=uu_{x}-\pi\operatorname{sen}(\pi x)\left[\pi+\cos(\pi x)\right].

(5.111)

Com isso, calculamos

	$\displaystyle f_{u}(x,u,u_{x})=u_{x},$		(5.112a)
	$\displaystyle f_{u_{x}}(x,u,u_{x})=u.$		(5.112b)

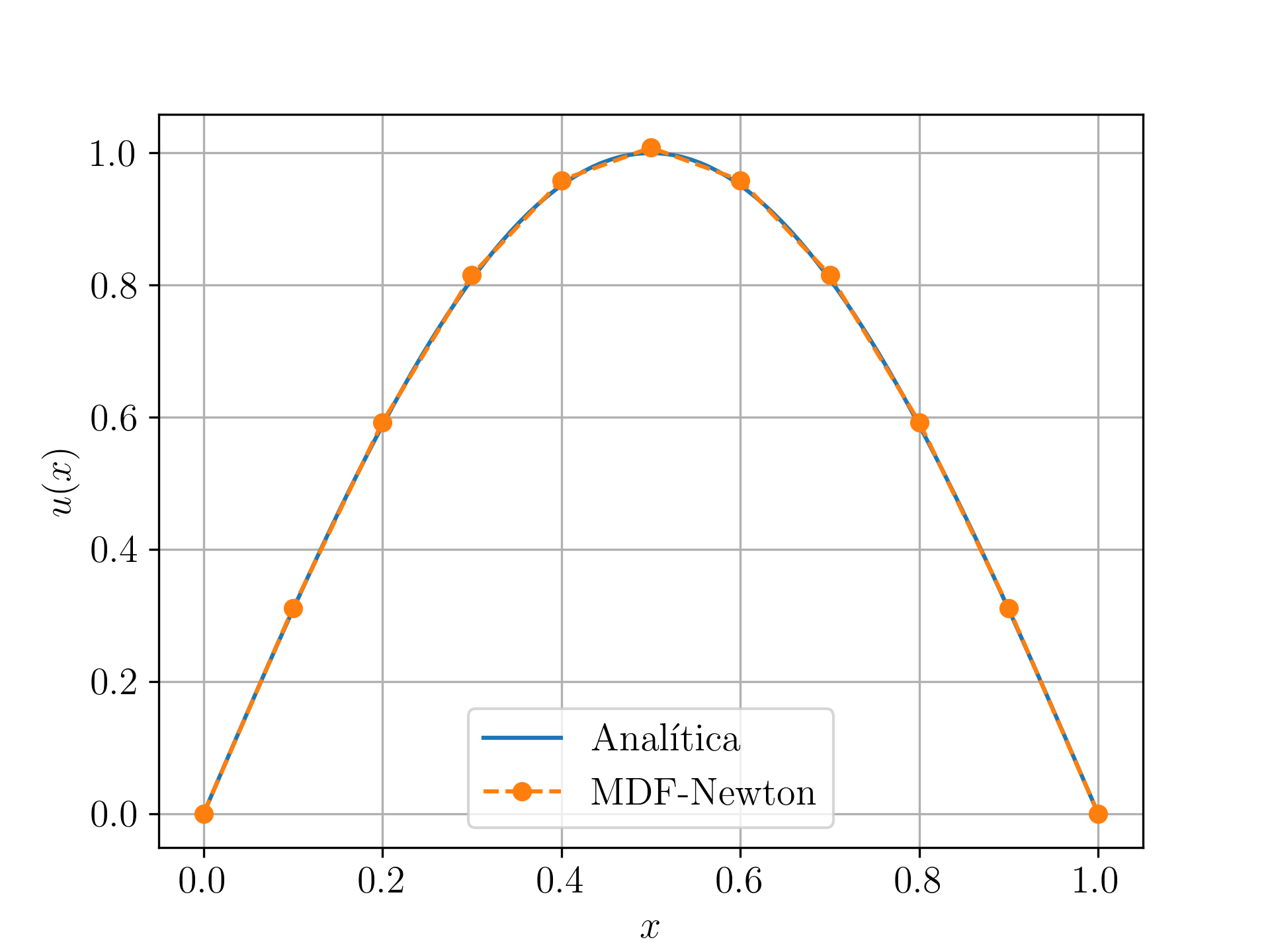
Então, a aplicação do MDF-Newton com $h=10^{-1}$ fornece o resultado da Fig. 5.4. A solução exata é $u(x)=\sin(\pi x)$ .

Refer to caption — Figura 5.4: Resultado da aplicação do MDF-Newton para o PVC do Ex. 5.4.1.

Código 19: mdf-newton.py

⬇

1import numpy as np

2import numpy.linalg as npla

3from numpy import pi, sin, cos

5# parâmetros

6n = 10

7h = 1./n

8xx = np.linspace(0., 1., n+1)

10# c.c. Dirichlet

11ua = 0.

12ub = 0.

14def f(x, u, ux):

15 return u*ux - pi*sin(pi*x)*(pi + cos(pi*x))

17def fu(x, u, ux):

18 return ux

20def fux(x, u, ux):

21 return u

23# rhs

24def F(u):

25 y = np.empty(n+1)

26 # f_1

27 y[0] = u[0] - ua

28 # f_i

29 for i in range(1,n):

30 ux = u[i+1]/(2*h) - u[i-1]/(2*h)

31 y[i] = -1./h**2*u[i-1] + 2./h**2*u[i] - 1./h**2*u[i+1] \

32 + f(xx[i], u[i], ux)

33 # f_{n+1}

34 y[n] = u[n] - ub

36 return y

38# jacobiana

39def J(u):

40 J = np.zeros((n+1,n+1))

41 J[0,0] = 1.

42 for i in range(1,n):

43 ux = 1./(2*h)*u[i+1] - 1./(2*h)*u[i-1]

44 J[i,i-1] = -1./h**2 - 1/(2*h)\

45 * fux(xx[i], u[i], ux)

46 J[i,i] = 2/h**2 + fu(xx[i], u[i], ux)

47 J[i,i+1] = -1./h**2 + 1/(2*h)\

48 * fux(xx[i], u[i], ux)

49 J[n,n] = 1.

51 return J

53# aprox inicial

54u = np.zeros(n+1)

56# iterações de Newton

57maxiter = 10

58for k in range(maxiter):

60 # passo de Newton

61 dlta = npla.solve(J(u), -F(u))

63 # atualização

64 u += dlta

66 ndlta = npla.norm(dlta)

67 print(f'{k+1}: norm = {ndlta:.2e}')

68 if (ndlta < 1e-10):

69 print('convergiu.')

70 break

5.4.1 Exercícios

E. 5.4.1.

Considere o PVC

	$\displaystyle u^{2}-u_{xx}=\cos^{2}(\pi x)+\pi^{2}\cos(\pi x),\leavevmode% \nobreak\ 0<x<1,$		(5.113a)
	$\displaystyle u(0)=1,$		(5.113b)
	$\displaystyle u(1)=-1.$		(5.113c)

Este problema tem solução analítica $u(x)=\cos(\pi x)$ . Use o MDF-Newton para computar $u_{h}$ aproximações de $u$ para $h=10^{-1}$ , $10^{-2}$ , $10^{-3}$ , $10^{-4}$ . Então, verifique a convergência com base no erro $\varepsilon_{h}:=\|\tilde{\boldsymbol{u}}-\boldsymbol{u}\|_{2}$ . A convergência tem a taxa esperada? Justifique sua resposta.

Resposta.

$h$	$\varepsilon_{h}$
$10^{-1}$	$4.0\mathrm{e}\!-\!03$
$10^{-2}$	$1.3\mathrm{e}\!-\!04$
$10^{-3}$	$4.0\mathrm{e}\!-\!06$
$10^{-4}$	$1.3\mathrm{e}\!-\!07$

E. 5.4.2.

Considere o PVC

	$\displaystyle uu_{x}-u_{xx}=2+x(1-x)(1-2x),\leavevmode\nobreak\ 0<x<1,$		(5.114a)
	$\displaystyle u_{x}(0)=1,$		(5.114b)
	$\displaystyle u(1)=0.$		(5.114c)

Este problema tem solução analítica $u(x)=x(1-x)$ . Use o MDF-Newton para computar $u_{h}$ aproximações de $u$ para $h=10^{-1}$ , $10^{-2}$ , $10^{-3}$ :

a)

aplicando as diferenças finitas $D_{0,h^{2}}u(x)$ para $0<x<1$ e $D_{+,h}u(x)$ para $x=0$ .
b)

aplicando as diferenças finitas $D_{0,h^{2}}u(x)$ para $0<x<1$ e $D_{+,h^{2}}u(x)$ para $x=0$ .

Qual dessas formulações tem a melhor taxa de convergência do erro em relação ao passo de malha $h$ ? Justifique e verifique sua resposta.

Resposta.

b) tem melhor taxa de convergência.

E. 5.4.3.

Desenvolva uma versão do método MEF-Newton (Método de Elementos Finitos com o Método de Newton) para computar a solução aproximada do PVC dado no Exemplo 5.4.1. Implemente-o e verifique a convergência do método para $h=10^{-1}$ , $10^{-2}$ e $10^{-3}$ .

E. 5.4.4.

Desenvolva uma versão do método MVF-Newton (Método de Volumes Finitos com o Método de Newton) para computar a solução aproximada do PVC dado no Exemplo 5.4.1. Implemente-o e verifique a convergência do método para $h=10^{-1}$ , $10^{-2}$ e $10^{-3}$ .

E. 5.4.5.

Desenvolva uma versão do método MEF-Newton (Método de Elementos Finitos com o Método de Newton) para computar a solução aproximada do PVC dado no Exercício 5.4.2. Implemente-o e verifique a convergência do método para $h=10^{-1}$ , $10^{-2}$ e $10^{-3}$ .

E. 5.4.6.

Desenvolva uma versão do método MVF-Newton (Método de Volumes Finitos com o Método de Newton) para computar a solução aproximada do PVC dado no Exercício 5.4.2. Implemente-o e verifique a convergência do método para $h=10^{-1}$ , $10^{-2}$ e $10^{-3}$ .

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |