| | | | |

1.1 Derivadas de Primeira Ordem

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

A derivada de uma função f num ponto x é, por definição,

f′⁢(x):=limh→0f⁢(x+h)−f⁢(x)h. (1.1)

Assim sendo e assumindo h>011endnote: 1Para fixar notação, assumiremos h>0 ao longo deste capítulo. próximo de zero, temos que f′⁢(x) pode ser aproximada pela fórmula de diferenças finitas

f′⁢(x) ≈f⁢(x+h)−f⁢(x)h (1.2a)
=:Dhf(x). (1.2b)

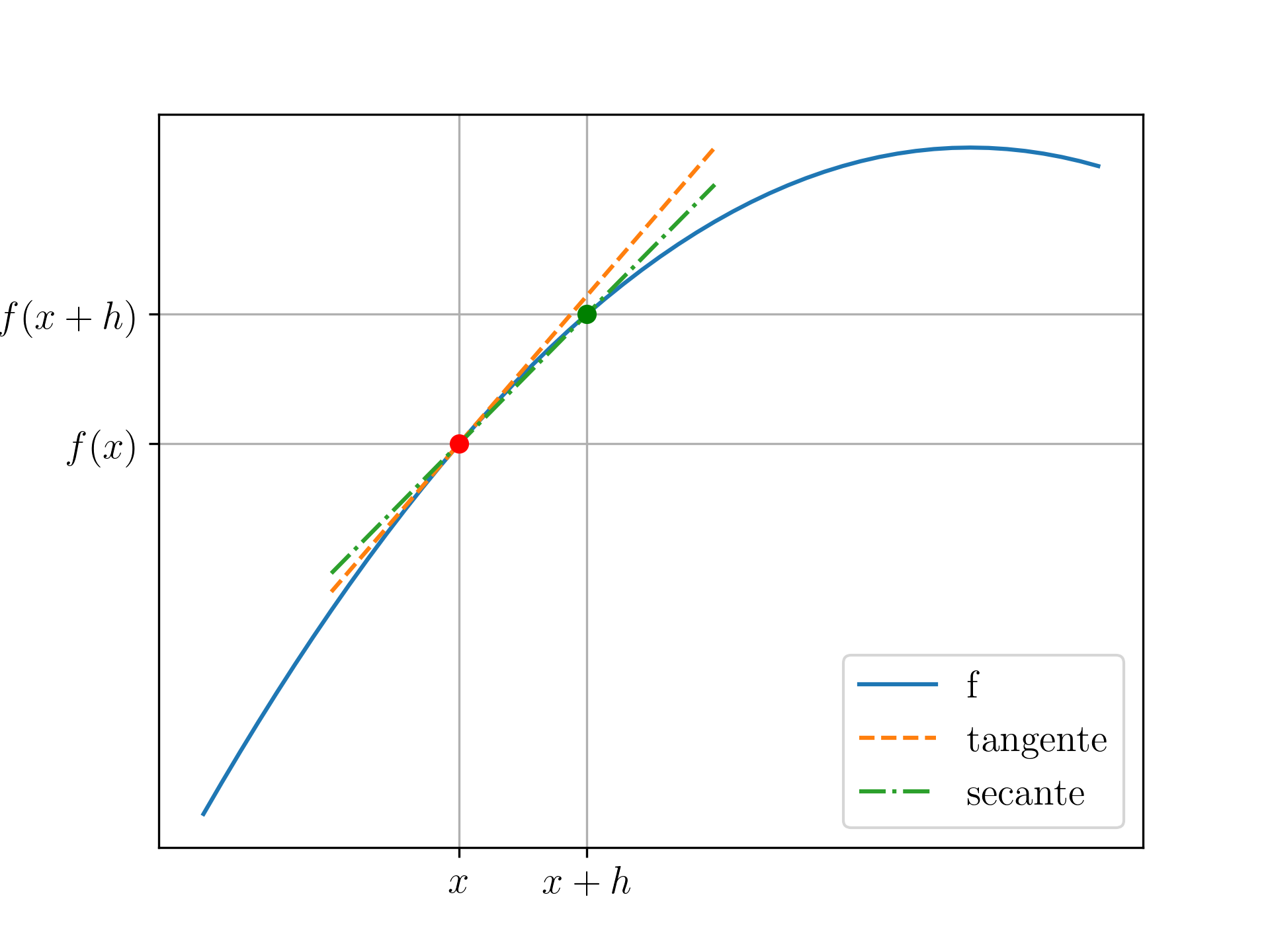
Geometricamente, isto é análogo a aproximar a declividade da reta tangente ao gráfico da função f no ponto (x,f⁢(x)) pela declividade da reta secante ao gráfico da função f pelos pontos (x,f⁢(x)) e (x+h,f⁢(x+h)) (consulte a Figura 1.1).

Refer to caption
Figura 1.1: Interpretação geométrica da aproximação da derivada pela razão fundamental.
Exemplo 1.1.1.

A derivada de f⁢(x)=sen⁡(x) no ponto π/3 é f′⁢(π/3)=cos⁡(π/3)=0.5. Agora, usando a aproximação pela fórmula de diferenças finitas (1.1), temos

f′⁢(π3) ≈Dh⁢f⁢(π3) (1.3a)
=f⁢(π3+h)−f⁢(π3)h (1.3b)
=sen⁡(π3+h)−sen⁡(π3)h. (1.3c)

Na Tabela 1.1 temos os valores desta aproximação para diferentes escolhas da passo h.

Tabela 1.1: Valores aproximados da derivada de f⁢(x)=sen⁡(x) no ponto x=π/3 usado a fórmula de diferenças finitas (1.1).
h D⁢f⁢(π/3)
10−1 4.55902⁢e−1
10−2 4.95662⁢e−1
10−3 4.99567⁢e−1
10−5 4.99996⁢e−1
10−7 5.00000⁢e−1
10−10 5.00000⁢e−1
⬇
1import numpy as np
2
3def dfdx(f, x, h=1e-7):
4    df = (f(x+h) - f(x))/h
5    return df
6
7f = lambda x: np.sin(x)
8x = np.pi/3
9h = 1e-7
10dfdx = dfdx(f, x, h)

1.1.1 Diferenças Finitas por Polinômio de Taylor

Vamos estudar o desenvolvimento de fórmulas de diferenças finitas via polinômios de Taylor.

Fórmula de Diferenças Finitas Progressiva de Ordem h

A aproximação por polinômio de Taylor de grau 1 de uma dada função f em torno no ponto x é

f⁢(x+h)=f⁢(x)+h⁢f′⁢(x)+O⁢(h2). (1.4)

Isolando f′⁢(x), obtemos

f′⁢(x)=f⁢(x+h)−f⁢(x)h+O⁢(h). (1.5)

Isto nos fornece a chamada fórmula de diferenças finitas progressiva de ordem h

D+,h⁢f⁢(x):=f⁢(x+h)−f⁢(x)h. (1.6)

Observemos que a ordem da fórmula se refere a do erro de truncamento com respeito ao passo h.

Exemplo 1.1.2.

Consideremos o problema de aproximar a derivada da função f⁢(x)=sen⁡(x) no ponto π/3. Usando a fórmula de diferenças finitas progressiva de ordem h obtemos

f′⁢(π3) ≈D+,h⁢f⁢(x) (1.7a)
=f⁢(π3+h)−f⁢(π3)h (1.7b)
=sen⁡(π3+h)−sen⁡(π3)h. (1.7c)

Na Tabela 1.2 temos os valores desta aproximação para diferentes escolhas de h, bem como, o erro absoluto da aproximação de f′⁢(π/3) por D+,h⁢f⁢(π/3).

Tabela 1.2: Resultados referente ao Exemplo 1.1.2.
h D+,h⁢f⁢(π/3) |f′⁢(π/3)−D+,h⁢f⁢(π/3)|
10−1 4.55902⁢e−1 4.4⁢e−2
10−2 4.95662⁢e−1 4.3⁢e−3
10−3 4.99567⁢e−1 4.3⁢e−4
10−5 4.99996⁢e−1 4.3⁢e−6
10−10 5.00000⁢e−1 4.1⁢e−8
Código 1: dfp_h.py
⬇
1import numpy as np
2
3def dfp_h(f, x, h=1e-7):
4    df = (f(x+h) - f(x))/h
5    return df
6
7f = lambda x: np.sin(x)
8x = np.pi/3
9h = 1e-1
10dfdx = dfp_h(f, x, h)
Observação 1.1.1.

(Erro de Truncamento.) No Exemplo 1.1.2, podemos observar que o erro absoluto na aproximação de f′⁢(x) por D+,h⁢f⁢(x) decresce conforme a ordem do erro de truncamento para valores moderados de h (consulte a Tabela 1.2). Agora, para valores de h muito pequenos (por exemplo, h=10−10), o erro |f′⁢(x)−D+,h⁢f⁢(x)| não segue mais a tendência de decaimento na mesma ordem do de truncamento. Isto se deve a dominância dos erros de arredondamento para valores muito pequenos de h.

Fórmula de Diferenças Finitas Regressiva de Ordem h

Substituindo h por −h no polinômio de Taylor de grau 1 (1.4), temos

f⁢(x−h)=f⁢(x)−h⁢f′⁢(x)+O⁢(h2), (1.8)

donde obtemos a fórmula de diferenças finitas regressiva de ordem h

D−,h⁢f⁢(x):=f⁢(x)−f⁢(x−h)h. (1.9)
Exemplo 1.1.3.

Consideremos o problema de aproximar a derivada da função f⁢(x)=sen⁡(x) no ponto π/3. Usando a fórmula de diferenças finitas regressiva de ordem h obtemos

f′⁢(π3) ≈D−,h⁢f⁢(x) (1.10a)
=f⁢(π3)−f⁢(π3−h)h (1.10b)
=sen⁡(π3)−sen⁡(π3−h)h. (1.10c)

Na Tabela 1.3 temos os valores desta aproximação para diferentes escolhas de h, bem como, o erro absoluto da aproximação de f′⁢(π/3) por D−,h⁢f⁢(π/3).

Tabela 1.3: Resultados referente ao Exemplo 1.1.3.
h D−,h⁢f⁢(π/3) |f′⁢(π/3)−D−,h⁢f⁢(π/3)|
10−1 5.42432⁢e−1 4.2⁢e−2
10−2 5.04322⁢e−1 4.3⁢e−3
10−3 5.00433⁢e−1 4.3⁢e−4
10−5 5.00004⁢e−1 4.3⁢e−6
10−10 5.00000⁢e−1 4.1⁢e−8
Código 2: dfr_h.py
⬇
1import numpy as np
2
3def dfr_h(f, x, h=1e-7):
4    df = (f(x) - f(x-h))/h
5    return df
6
7f = lambda x: np.sin(x)
8x = np.pi/3
9h = 1e-1
10dfdx = dfr_h(f, x, h)

Fórumla de Diferenças Finitas Central de Ordem h2

Usando o polinômio de Taylor de grau 2 para aproximar a função f⁢(x) em torno de x, temos

f⁢(x+h) =f⁢(x)+h⁢f′⁢(x)+h2⁢f′′⁢(x)+O⁢(h3) (1.11)
f⁢(x−h) =f⁢(x)−h⁢f′⁢(x)+h2⁢f′′⁢(x)+O⁢(h3). (1.12)

Então, subtraindo esta segunda equação da primeira, temos

f⁢(x+h)−f⁢(x−h)=2⁢h⁢f′⁢(x)+O⁢(h3). (1.13)

Então, isolando f⁢(x), obtemos

f′⁢(x)=f⁢(x+h)−f⁢(x−h)2⁢h+O⁢(h2), (1.14)

Isto nos fornece a chamada fórmula de diferenças finitas central de ordem h2

D0,h2⁢f⁢(x):=f⁢(x+h)−f⁢(x−h)2⁢h. (1.15)
Exemplo 1.1.4.

Consideremos o problema de aproximar a derivada da função f⁢(x)=sen⁡(x) no ponto π/3. Usando a fórmula de diferenças finitas central de ordem h2 obtemos

f′⁢(π3) ≈D0,h2⁢f⁢(x) (1.16a)
=f⁢(π3+h)−f⁢(π3−h)2⁢h (1.16b)
=sen⁡(π3+h)−sen⁡(π3−h)2⁢h. (1.16c)

Na Tabela 1.4 temos os valores desta aproximação para diferentes escolhas de h, bem como, o erro absoluto da aproximação de f′⁢(π/3) por D0,h2⁢f⁢(π/3).

Tabela 1.4: Resultados referente ao Exemplo 1.1.4.
h D0,h2⁢f⁢(π/3) |f′⁢(π/3)−D0,h2⁢f⁢(π/3)|
10−1 4.99167⁢e−1 8.3⁢e−04
10−2 4.99992⁢e−1 8.3⁢e−06
10−3 5.00000⁢e−1 8.3⁢e−08
10−5 5.00000⁢e−1 8.3⁢e−10
10−10 5.00000⁢e−1 7.8⁢e−12
Código 3: dfc_h2.py
⬇
1import numpy as np
2
3def dfc_h2(f, x, h=1e-7):
4    df = (f(x+h) - f(x-h))/(2*h)
5    return df
6
7f = lambda x: np.sin(x)
8x = np.pi/3
9h = 1e-1
10dfdx = dfc_h2(f, x, h)

Exercícios

E. 1.1.1.

Considere a função f⁢(x)=cos⁡(x). Use a fórmula de diferenças finitas progressiva de ordem h para computar a aproximação de f′⁢(π/3) com 5 dígitos significativos corretos.

Resposta.

f′⁢(π/3)=−0.866025⁢e+0,h=10−7

E. 1.1.2.

Considere a função f⁢(x)=cos⁡(x). Use a fórmula de diferenças finitas regressiva de ordem h para computar a aproximação de f′⁢(π/3) com 5 dígitos significativos corretos.

Resposta.

f′⁢(π/3)=−0.866025⁢e+0,h=10−6

E. 1.1.3.

Considere a função f⁢(x)=cos⁡(x). Use a fórmula de diferenças finitas central de ordem h2 para computar a aproximação de f′⁢(π/3) com 5 dígitos significativos corretos.

Resposta.

f′⁢(π/3)=−0.866025⁢e+0,h=10−3

E. 1.1.4.

Calcule aproximações da derivada de

f⁢(x)=sen⁡(x+2)−e−x2x2+ln⁡(x+2)+x (1.17)

no ponto x=2.5 dadas pelas seguintes fórmulas de diferenças finitas com h=10−2:

  1. a)

    progressiva de ordem h.

  2. b)

    regressiva de ordem h.

  3. c)

    central de ordem h2.

Resposta.

a) D+,h⁢f⁢(2.5)=1,05949; b) D−,h⁢f⁢(2.5)=1,05877; c) D0,h2⁢f⁢(2.5)=1,05913;

E. 1.1.5.

Considere a seguinte tabela de pontos

i xi yi
1 2.0 1.86
2 2.1 1.90
3 2.2 2.01
4 2.3 2.16
5 2.4 2.23
6 2.5 2.31

Calcule aproximações de d⁢y/d⁢x usando diferenças finitas centrais de ordem h2 quando possível e, caso contrário, diferenças finitas progressiva ou regressiva conforme o caso.

Resposta.
i d⁢y/d⁢x
1 4.0⁢e−2
2 7.5⁢e−1
3 1.3⁢e+0
4 1.1⁢e+0
5 7.5⁢e−1
6 8.0⁢e−1
E. 1.1.6.

Use uma combinação de polinômios de Taylor de grau 2 para desenvolver a fórmula de diferenças finitas progressiva de ordem h2

D+,h2⁢(x):=12⁢h⁢[−3⁢f⁢(x)+4⁢f⁢(x+h)−f⁢(x+2⁢h)]. (1.18)

Então, aplique-a para computar f′⁢(π/3) com f⁢(x)=sen⁡(x) e verifique o comportamento do erro |D+,h2⁢(π/3)−f′⁢(π/3)| em relação à ordem de truncamento da fórmula.

E. 1.1.7.

Use uma combinação de polinômios de Taylor de grau 2 para desenvolver a fórmula de diferenças finitas regressiva de ordem h2

D−,h2⁢(x):=12⁢h⁢[3⁢f⁢(x)−4⁢f⁢(x−h)+f⁢(x−2⁢h)]. (1.19)

Então, aplique-a para computar f′⁢(π/3) com f⁢(x)=sen⁡(x) e verifique o comportamento do erro |D+,h2⁢(π/3)−f′⁢(π/3)| em relação à ordem de truncamento da fórmula.

E. 1.1.8.

Refaça as computações do Exercício 1.1.5 usando fórmulas de diferenças finitas de ordem h2 para todos os pontos.

Resposta.
i d⁢y/d⁢x
1 5.0⁢e−2
2 7.5⁢e−1
3 1.3⁢e+0
4 1.1⁢e+0
5 7.5⁢e−1
6 8.5⁢e−1

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |