Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

2 Derivadas 2.4 Derivada de Funções Exponenciais e Logarítmicas 2.6 Derivadas de funções trigonométricas

2.5 Regas Básicas de Derivação

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.5.1 Regras da multiplicação por constante e da soma

Sejam $k$ um número real, $u=u(x)$ e $v=v(x)$ funções deriváveis. Temos as seguintes regras básicas de derivação:

•

$\boldsymbol{(k\cdot u)^{\prime}=k\cdot u^{\prime}}$ .

De fato, pela definição da derivada temos

$\displaystyle(k\cdot u)^{\prime}(x)$ $\displaystyle=\lim_{h\to 0}\frac{k\cdot u(x+h)-k\cdot u(x)}{h}$ (2.235)

$\displaystyle=\lim_{h\to 0}k\cdot\left(\frac{u(x+h)-u(x)}{h}\right)$ (2.236)

$\displaystyle=k\cdot\lim_{h\to 0}\cancelto{u^{\prime}}{\frac{u(x+h)-u(x)}{h}}$ (2.237)

$\displaystyle=k\cdot u^{\prime}.$ (2.238)

No SymPy, podemos usar os seguintes comandos para obtermos esta regra de derivação:

Código 40: Python

⬇

1    from sympy import *

2    k = Symbol('k', real=True)

3    u = Function('u', real=True)

4    diff(k*u(x),x)

•

$\boldsymbol{(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}}$ .

De fato, temos

$\displaystyle(u+v)^{\prime}(x)$	$\displaystyle=\lim_{h\to 0}\frac{(u+v)(x+h)-(u+v)(x)}{h}$	(2.239)
	$\displaystyle=\lim_{h\to 0}\frac{u(x+h)+v(x+h)-[u(x)+v(x)]}{h}$	(2.240)
	$\displaystyle=\lim_{h\to 0}\left[\cancelto{u^{\prime}}{\frac{u(x+h)-u(x)}{h}}\right.$	(2.241)
	$\displaystyle+\left.\cancelto{v^{\prime}}{\frac{v(x+h)-v(x)}{h}}\right]$	(2.242)
	$\displaystyle=u^{\prime}(x)+v^{\prime}(x).$	(2.243)

Também, como $(-v)^{\prime}=(-1\cdot v)^{\prime}=-1\cdot v^{\prime}=-v^{\prime}$ , temos

(u-v)^{\prime}=[u+(-v)]^{\prime}=u^{\prime}+(-v)^{\prime}=u^{\prime}-v^{\prime}.

(2.244)

No SymPy, podemos usar os seguintes comandos para obtermos a regra de derivação para soma:

Código 41: Python

⬇

1 from sympy import *

2 u = Function('u', real=True)

3 v = Function('v', real=True)

4 diff(u(x)+v(x),x)

Exemplo 2.5.1.

Vejamos os seguintes casos:

a)

$f(x)=2x$ .

Para calcularmos $f^{\prime}$ , podemos identificar $f=k\cdot u$ , com $k=2$ e $u(x)=x$ . Então, usando a regra da multiplicação por constante $(ku)^{\prime}=ku^{\prime}$ , temos

$f^{\prime}(x)=(2x)^{\prime}=2(x^{\prime})=2\cdot 1=2.$ (2.245)

No SymPy, podemos computar esta derivada com o comando:

Código 42: Python

⬇

1    from sympy import *

2    x = Symbol('x')

3    diff(2*x,x)
b)

$f(x)=2x+3$ .

Observamos que $f=u+v$ , com $u(x)=2x$ e $v(x)\equiv 3$ . Então, da regra da soma $(u+v)^{\prime}=u^{\prime}+v^{\prime}$ , temos

$f^{\prime}(x)=(2x+3)^{\prime}=(2x)^{\prime}+(3)^{\prime}=2+0=2.$ (2.246)

No SymPy, podemos computar esta derivada com o comando:

Código 43: Python

⬇

1      from sympy import *

2      x = Symbols('x')

3      diff(2*x+3,x)
c)

$f(x)=e^{x}-x^{2}$ .

Observamos que $f=u-v$ , com $u(x)=e^{x}$ e $v(x)=x^{2}$ . Usando a regra da subtração $(u-v)^{\prime}=u^{\prime}-v^{\prime}$ temos

$f^{\prime}(x)=(e^{x}-x^{2})^{\prime}=(e^{x})^{\prime}-(x^{2})^{\prime}=e^{x}-2x.$ (2.247)

No SymPy, podemos computar esta derivada com o comando:

Código 44: Python

⬇

1      from sympy import *

2      x = Symbols('x')

3      diff(exp(x)-x**2,x)

2.5.2 Regras do produto e do quociente

Sejam $y=u(x)$ e $y=v(x)$ funções deriváveis. Então:

•

$\boldsymbol{(u\cdot v)^{\prime}=u^{\prime}\cdot v+u\cdot v^{\prime}}$ .

De fato, da definição da derivada temos

$\displaystyle(uv)^{\prime}(x)$	$\displaystyle=\lim_{h\to 0}\frac{(uv)(x+h)-(uv)(x)}{h}$	(2.248)
	$\displaystyle=\lim_{h\to 0}\frac{u(x+h)v(x+h)-u(x)v(x)}{h}$	(2.249)
	$\displaystyle=\lim_{h\to 0}\left[\frac{u(x+h)v(x+h)-u(x)v(x+h)}{h}\right.$	(2.250)
	$\displaystyle\qquad\quad+\left.\frac{u(x)v(x+h)-u(x)v(x)}{h}\right]$	(2.251)
	$\displaystyle=\lim_{h\to 0}\frac{u(x+h)-u(x)}{h}v(v+h)$	(2.252)
	$\displaystyle+\lim_{h\to 0}u(x)\frac{v(x+h)-v(x)}{h}$	(2.253)
	$\displaystyle=u^{\prime}(x)v(x)+u(x)v^{\prime}(x).$	(2.254)

No SymPy, podemos usar os seguintes comandos para obtermos tal regra de derivação:

Código 45: Python

⬇

1 u = Function('u', real=True)

2 v = Function('v', real=True)

3 diff(u(x)*v(x), x)

•

$\displaystyle\boldsymbol{\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-% uv^{\prime}}{v^{2}}}$ , no caso de $v(x)\neq 0$ .

De fato, da definição de derivada temos

$\displaystyle\left(\frac{u}{v}\right)^{\prime}(x)$	$\displaystyle=\lim_{h\to 0}\frac{\left(\frac{u}{v}\right)(x+h)-\left(\frac{u}{% v}\right)(x)}{h}$	(2.255)
	$\displaystyle=\lim_{h\to 0}\frac{\frac{u(x+h)v(x)-u(x)v(x+h)}{v(x+h)v(x)}}{h}$	(2.256)
	$\displaystyle=\lim_{h\to 0}\left[\frac{u(x+h)v(x)-u(x)v(x)}{h}\right.$	(2.257)
	$\displaystyle\qquad\quad-\left.\frac{u(x)v(x+h)-u(x)v(x)}{h}\right]\frac{1}{v(% x)v(x+h)}$	(2.258)
	$\displaystyle=\left[\lim_{h\to 0}\cancelto{u^{\prime}(x)v(x)}{\frac{u(x+h)-u(x% )}{h}v(x)}\right.$	(2.259)
	$\displaystyle\left.-\lim_{h\to 0}\cancelto{u(x)v^{\prime}(x)}{u(x)\frac{v(x+h)% -v(x)}{h}}\right]\lim_{h\to 0}\cancelto{\frac{1}{v^{2}(x)}}{\frac{1}{v(x)v(x+h% )}}$	(2.260)
	$\displaystyle=\frac{u^{\prime}(x)v(x)-u(x)v^{\prime}(x)}{v^{2}(x)}.$	(2.261)

No SymPy, podemos usar os seguintes comandos para obtermos tal regra de derivação:

Código 46: Python

⬇

1 from sympy import *

2 x = Symbol('x')

3 u = Function('u', real=True)

4 v = Function('v', real=True)

5 simplify(diff(u(x)/v(x),x))

Exemplo 2.5.2.

Vamos calcular a derivada em relação a $x$ da função $f(x)=x^{2}(x-1)$ de duas formas.

1.

Por expansão da expressão e utilização da regra da subtração.

$\displaystyle f^{\prime}(x)$ $\displaystyle=[x^{2}(x-1)]^{\prime}$ (2.262)

$\displaystyle=(x^{3}-x^{2})^{\prime}$ (2.263)

$\displaystyle=\overbrace{(x^{3})^{\prime}-(x^{2})^{\prime}}^{(u-v)^{\prime}=u^% {\prime}-v^{\prime}}$ (2.264)

$\displaystyle=3x^{2}-2x,\quad\quad(x^{n})^{\prime}=nx^{n-1}.$ (2.265)
2.

Utilizando a regra do produto.

Observamos que $f=u\cdot v$ , com $u(x)=x^{2}$ e $v(x)=x-1$ . Então, da regra do produto $(uv)^{\prime}=u^{\prime}v+uv^{\prime}$ , com $u^{\prime}(x)=2x$ e $v^{\prime}(x)=1$ , temos

$\displaystyle f^{\prime}(x)$ $\displaystyle=[\overbrace{x^{2}}^{u}\overbrace{(x-1)}^{v}]^{\prime}$ (2.266)

$\displaystyle=\overbrace{2x\cdot(x-1)}^{u^{\prime}\cdot v}+\overbrace{x^{2}% \cdot 1}^{u\cdot v^{\prime}}$ (2.267)

$\displaystyle=2x^{2}-2x+x^{2}$ (2.268)

$\displaystyle=3x^{2}-2x.$ (2.269)

Exemplo 2.5.3.

Vamos calcular a derivada em relação a $x$ de $f(x)=1/x^{2}$ para $x\neq 0$ . Observamos que $f=(u/v)$ com $u(x)\equiv 1$ e $v(x)=x^{2}$ . Tendo em vista que $u^{\prime}(x)\equiv 0$ e $v^{\prime}(x)=2x$ , temos da regra do quociente que

$\displaystyle f^{\prime}(x)$	$\displaystyle=\left(\frac{1}{x^{2}}\right)^{\prime}$	(2.270)
	$\displaystyle=\frac{0\cdot x^{2}-1\cdot 2x}{(x^{2})^{2}},\quad\quad\left[\left% (\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{v^{2}}\right]$	(2.271)
	$\displaystyle=-\frac{2x}{x^{4}}=-\frac{2}{x^{3}}$	(2.272)
	$\displaystyle=-2x^{-3}.$	(2.273)

Observação 2.5.1.

Com abuso de linguagem, temos

\boldsymbol{(x^{n})^{\prime}=nx^{n-1}},

(2.274)

com $n$ inteiro. No caso de $n=1$ , temos $(x)^{\prime}\equiv 1$ . No caso de $n<=0$ , devemos ter $x\neq 0$ ¹⁷¹⁷endnote: ¹⁷Devido a indeterminação de $0^{0}$ e a inexistência de $0^{n}$ com $n$ negativo. Mais ainda, a regra também vale para $n=1/2$ , veja o Exemplo 2.2.2.

Exemplo 2.5.4.

Voltando ao exemplo anterior (Exemplo 2.5.3), temos

\left(\frac{1}{x^{2}}\right)^{\prime}=\overbrace{(x^{-2})^{\prime}}^{(x^{n})^{% \prime}}=\overbrace{-2x^{-2-1}}^{nx^{n-1}}=-2x^{-3}.

(2.275)

Exemplo 2.5.5.

Vamos calcular a derivada em relação a $x$ de $f(x)=xe^{x}$ . Usando a regra do produto $(uv)^{\prime}=u^{\prime}v+uv^{\prime}$ com $u(x)=x$ e $v(x)=e^{x}$ , temos

$\displaystyle f^{\prime}(x)$	$\displaystyle=\overbrace{(xe^{x})^{\prime}}^{(uv)^{\prime}}$	(2.276)
	$\displaystyle=\overbrace{1\cdot e^{x}}^{u^{\prime}\cdot v}+\overbrace{x\cdot e% ^{x}}^{u\cdot v^{\prime}}$	(2.277)
	$\displaystyle=(x+1)e^{x}.$	(2.278)

2.5.3 Lista de derivadas

	$\displaystyle(k\cdot u)^{\prime}=k\cdot u^{\prime}$		(2.279)
	$\displaystyle(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}$		(2.280)
	$\displaystyle(uv)^{\prime}=u^{\prime}v+uv^{\prime}$		(2.281)
	$\displaystyle\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{% v^{2}}$		(2.282)
	$\displaystyle(k)^{\prime}=0$		(2.283)
	$\displaystyle(x)^{\prime}=1$		(2.284)
	$\displaystyle(x^{n})^{\prime}=nx^{n-1}$		(2.285)
	$\displaystyle(a^{x})^{\prime}=a^{x}\ln a$		(2.286)
	$\displaystyle(e^{x})^{\prime}=e^{x}$		(2.287)
	$\displaystyle(\log_{a}x)^{\prime}=\frac{1}{x\ln a}$		(2.288)
	$\displaystyle(\ln x)^{\prime}=\frac{1}{x}$		(2.289)

2.5.4 Exercícios resolvidos

ER 2.5.1.

Calcule a derivada em relação a $x$ da função

f(x)=(x^{2}+x)(1+x^{3})-2x^{2}.

(2.290)

Solução.

$\displaystyle f^{\prime}(x)$	$\displaystyle=\overbrace{\left[(x^{2}+x)(1+x^{3})-2x^{2}\right]^{\prime}}^{(u-% v)^{\prime}}$	(2.291)
	$\displaystyle=\overbrace{\left[(x^{2}+x)(1+x^{3})\right]^{\prime}}^{(uv)^{% \prime}}-\overbrace{(2x^{2})^{\prime}}^{(ku)^{\prime}}$	(2.292)
	$\displaystyle=(x^{2}+x)^{\prime}(1+x^{3})+(x^{2}+x)(1+x^{3})^{\prime}-2(x^{2})% ^{\prime}$	(2.293)
	$\displaystyle=(2x+1)(1+x^{3})+(x^{2}+x)3x^{2}-4x$	(2.294)
	$\displaystyle=2x+2x^{4}+1+x^{3}+3x^{4}+3x^{3}-4x$	(2.295)
	$\displaystyle=5x^{4}+4x^{3}-2x+1.$	(2.296)

Com o SymPy, podemos computar esta derivada com os seguintes comandos:

Código 47: Python

⬇

1 from sympy import *

2 x = Symbol('x')

3 d = diff((x**2+x)*(1+x**3)-2x^2,x)

4 simplify(d)

ER 2.5.2.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{x^{2}+x}{1-x^{3}}\right).

(2.297)

Solução.

Da regra de derivação do quociente, temos

$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{x^{2}+x}{1-x^{3}}\right)$	$\displaystyle=\frac{(x^{2}+x)^{\prime}(1-x^{3})-(x^{2}+x)(1-x^{3})^{\prime}}{(% 1-x^{3})^{2}}$	(2.298)
	$\displaystyle=\frac{(2x+1)(1-x^{3})+(x^{2}+x)3x^{2}}{1-2x^{3}+x^{6}}$	(2.299)
	$\displaystyle=\frac{2x-2x^{4}+1-x^{3}+3x^{4}+3x^{3}}{1-2x^{3}+x^{6}}$	(2.300)
	$\displaystyle=\frac{x^{4}+2x^{3}+2x+1}{x^{6}-2x^{3}+1}$	(2.301)

Com o SymPy, podemos computar esta derivada com os seguintes comandos:

Código 48: Python

⬇

1 from sympy import *

2 x = Symbol('x')

3 d = diff((x**2+x)/(1-x**3),x)

4 simplify(d)

ER 2.5.3.

Encontre a equação da reta tangente ao gráfico de $f(x)=xe^{-x}$ no ponto $x=1$ .

Solução.

A equação da reta tangente ao gráfico de uma função $f$ no ponto $x=x_{0}$ é

y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0}).

(2.302)

No caso, temos $f(x)=xe^{-x}$ e $x_{0}=1$ . Calculamos

$\displaystyle f^{\prime}(x)$	$\displaystyle=[xe^{-x}]^{\prime}=\left[\frac{x}{e^{x}}\right]$	(2.303)
	$\displaystyle=\frac{(x)^{\prime}e^{x}-x(e^{x})^{\prime}}{(e^{x})^{2}}$	(2.304)
	$\displaystyle=\frac{e^{x}-xe^{x}}{e^{2x}}$	(2.305)
	$\displaystyle=\frac{(1-x)e^{x}}{e^{2x}}$	(2.306)
	$\displaystyle=(1-x)e^{x}e^{-2x}=(1-x)e^{-x}.$	(2.307)

Logo, a equação da reta tangente é

	$\displaystyle y=f^{\prime}(1)(x-1)+f(1)$		(2.308)
	$\displaystyle y=0\cdot(x-1)+e^{-1}$		(2.309)
	$\displaystyle y=\frac{1}{e}.$		(2.310)

Na Figura 2.7, temos os esboços dos gráfico da função $f$ e sua reta tangente no ponto $x=1$ .

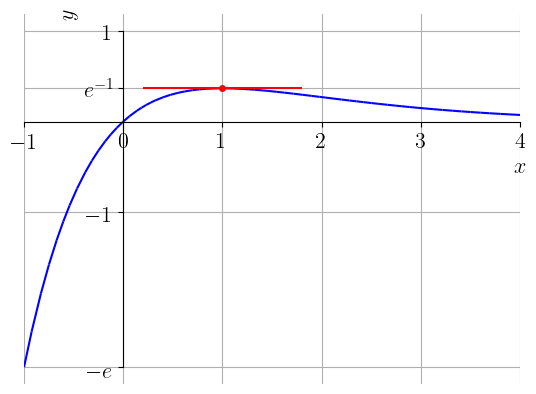
Refer to caption — Figura 2.7: Esboço da reta tangente ao gráfico de $f(x)=xe^{-x}$ no ponto $x=1$ .

Com o SymPy, podemos computar a expressão desta reta tangente com os seguintes comandos:

Código 49: Python

⬇

1 from sympy import *

2 x = Symbol('x')

3 f = x*exp(-x)

4 x0 = 1

5 fl = diff(f,x)

6 # y =

7 fl.subs(x,1)*(x-1)+f.subs(x,1)