Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Aplicações da derivada 3.3 Teorema do valor médio 3.5 Concavidade e o Teste da segunda derivada

3.4 Teste da primeira derivada

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Na Seção 3.2, vimos que os extremos de uma função ocorrem nos extremos de seu domínio ou em um ponto crítico. Aliado a isso, o Corolário 3.3.3 nos fornece condições suficientes para classificar os pontos críticos como extremos locais.

Mais precisamente, seja $c$ um ponto crítico de uma função contínua $f$ e diferenciável em todos os pontos de um intervalo aberto $(a,b)$ contendo $c$ , exceto possivelmente no ponto $c$ . Movendo-se no sentido positivo em $x$ :

•

se $f^{\prime}(x)$ muda de negativa para positiva em $c$ , então $f$ possui um mínimo local em $c$ ;
•

se $f^{\prime}(x)$ muda de positiva para negativa em $c$ , então $f$ possui um máximo local em $c$ ;
•

se $f^{\prime}$ não muda de sinal em $c$ , então $c$ não é um extremo local de $f$ .

Veja a Figura 3.14.

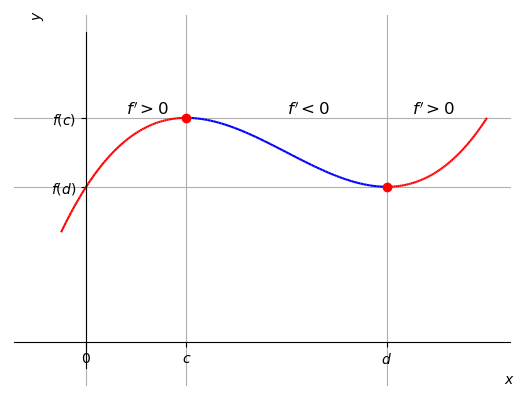
Refer to caption — Figura 3.14: Ilustração do teste da primeira derivada com $c$ ponto de máximo local e $d$ ponto de mínimo local.

Exemplo 3.4.1.

Consideremos a função $\displaystyle f(x)=\frac{x^{3}}{3}-2x^{2}+3x+3$ . Como $f$ é diferenciável em toda parte, seus pontos críticos são aqueles tais que

f^{\prime}(x)=0.

(3.72)

Temos $f^{\prime}(x)=x^{2}-4x+3$ . Segue, que os pontos críticos são

	$\displaystyle x^{2}-4x+3=0$	$\displaystyle\Rightarrow x=\frac{4\pm\cancelto{2}{\sqrt{16-12}}}{2}$		(3.73)
		$\displaystyle\Rightarrow x_{1}=1,\quad x_{2}=3.$		(3.74)

Com isso, temos

Intervalo	$x<1$	$1<x<3$	$3<x$
$f^{\prime}$	+	-	+
$f$	crescente	decrescente	crescente

Então, do teste da primeira derivada, concluímos que $x_{1}=1$ é ponto de máximo local e que $x_{2}=3$ é ponto de mínimo local.

Podemos usar o SymPy para computarmos a derivada de $f$ com o comando³⁰³⁰endnote: ³⁰Veja a Observação 3.0.1.

fl = diff(x**3/3-2*x**2+3*x+3)

Então, podemos resolver $f^{\prime}(x)=0$ com o comando

solve(fl)

e, por fim, podemos fazer o estudo de sinal da $f^{\prime}$ com os comandos

reduce_inequalities(fl<0)
reduce_inequalities(fl>0)

3.4.1 Exercícios resolvidos

ER 3.4.1.

Determine e classifique os extremos da função

f(x)=x^{4}-4x^{3}+4x^{2}.

(3.75)

Solução.

Como o domínio da $f$ é $(-\infty,\infty)$ e $f$ é diferenciável em toda parte, temos que seus extremos ocorrem em pontos críticos tais que

f^{\prime}(x)=0.

(3.76)

Resolvendo, obtemos

\displaystyle 4x^{3}-12x^{2}+8x=0

\displaystyle\Rightarrow 4x(x^{2}-3x+2)=0

(3.77)

Logo,

$\displaystyle 4x=0\quad\text{ou}\quad$	$\displaystyle x^{2}-3x+2=0$	(3.78)
$\displaystyle x_{1}=0$	$\displaystyle x=\frac{3\pm 1}{2}.$	(3.79)
	$\displaystyle x_{2}=1,\quad x_{3}=2$	(3.80)

Portanto, os ponto críticos são $x_{1}=0$ , $x_{2}=1$ e $x_{3}=2$ . Fazendo o estudo de sinal da $f^{\prime}$ , temos

	$x<0$	$0<x<1$	$1<x<2$	$2<x$
$4x$	-	+	+	+
$x^{2}-3x+2$	+	+	-	+
$f^{\prime}(x)$	-	+	-	+
$f$	decrescente	crescente	decrescente	crescente

Então, do teste da primeira derivada, concluímos que $x_{1}=0$ é ponto de mínimo local, $x_{2}=-2$ é ponto de máximo local e $x_{3}=-1$ é ponto de mínimo local.

Podemos usar os seguintes comandos do SymPy³¹³¹endnote: ³¹Veja a Observação 3.0.1. para resolvermos este exercício:

# f’
fl = Lambda(x, diff(x**4 - 4*x**3 + 4*x**2,x))
# f’(x) = 0
solve(fl(x))
# fl(x) < 0
reduce_inequalities(fl(x)<0)
# fl(x) > 0
reduce_inequalities(fl(x)>0)

ER 3.4.2.

Encontre o valor máximo global de $f(x)=(x-1)e^{-x}$ .

Solução.

Como $f$ é diferenciável em toda parte, temos que seu máximo ocorre em ponto crítico tal que

$\displaystyle f^{\prime}(x)=0$	$\displaystyle\Rightarrow(2-x)e^{-x}=0$	(3.81)
	$\displaystyle\Rightarrow 2-x=0$	(3.82)
	$\displaystyle\Rightarrow x=2.$	(3.83)

Fazendo o estudo de sinal da derivada, obtemos

	x<0	0<x
f’	+	-
f	crescente	decrescente

Portanto, do teste da primeira derivada, podemos concluir que $x=2$ é ponto de máximo local. O favor da função neste ponto é $f(2)=e^{-2}$ . Ainda, temos

	$\displaystyle\lim_{x\to-\infty}(x-1)e^{-x}=-\infty,$		(3.84)
	$\displaystyle\lim_{x\to\infty}(x-1)e^{-x}=0.$		(3.85)

Por tudo isso, concluímos que o valor máximo global de $f$ é $f(2)=e^{-2}$ .

Podemos usar os seguintes comandos do SymPy³²³²endnote: ³²Veja a Observação 3.0.1. para resolvermos este exercício:

# f(x)
f = Lambda(x, (x-1)*exp(-x))
# f’(x)
fl = Lambda(x, diff(f(x),x))
# pontos críticos
xc = solve(fl(x))
# f’(x) < 0
reduce_inequalities(fl(x)<0)
# f’(x) > 0
reduce_inequalities(fl(x)>0)
# lim f(x), x->-oo
limit(f(x),x,-oo)
# lim f(x), x->oo
limit(f(x),x,oo)
# f(2)
f(xc[0])

3.4.2 Exercícios

E. 3.4.1.

Use o teste da primeira derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $f(x)=x^{2}-2x$ .

Resposta.

$x=1$ ponto de mínimo global

E. 3.4.2.

Use o teste da primeira derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $\displaystyle f(x)=\frac{x^{3}}{3}-x$ .

Resposta.

$x_{1}=-1$ ponto de máximo local; $x_{2}=1$ ponto de mínimo local;

E. 3.4.3.

Use o teste da primeira derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $\displaystyle f(x)=x^{2/3}(x-1)$ .

Resposta.

$x_{1}=0$ ponto de máximo local; $x_{2}=2/5$ ponto de mínimo local;

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |