Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Aplicações da derivada 3.1 Regra de L’Hôpital 3.3 Teorema do valor médio

3.2 Extremos de funções

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Seja $f$ uma função com domínio $D$ . Dizemos que $f$ tem o valor máximo global²³²³endnote: ²³Também chamado de máximo absoluto. $f(a)$ no ponto $x=a$ quando

f(x)\leq f(a),

(3.41)

para todo $x\in D$ . Analogamente, dizemos que $f$ tem o valor mínimo global²⁴²⁴endnote: ²⁴Também chamado de mínimo absoluto. $f(b)$ no ponto $x=b$ quando

f(x)\geq f(b),

(3.42)

para todo $x\in D$ . Em tais pontos, dizemos que a função têm seus valores extremos globais (ou extremos absolutos).

Exemplo 3.2.1.

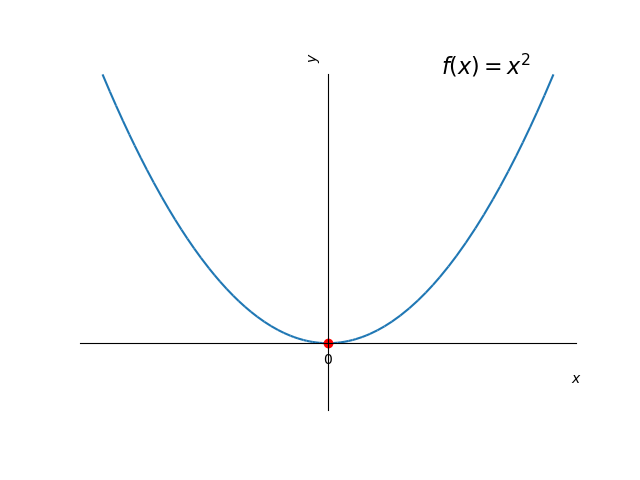
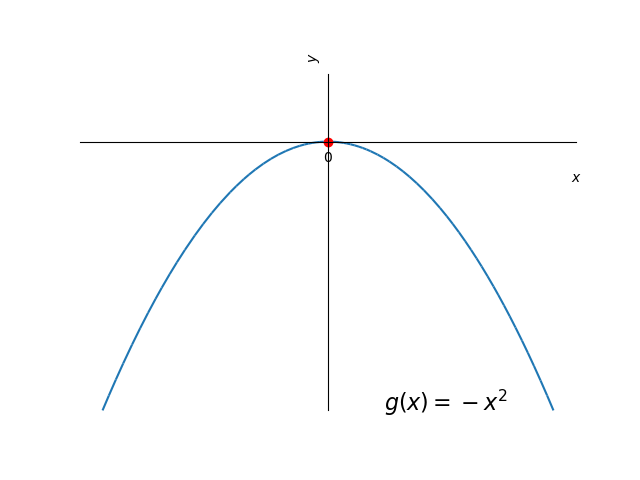
A função $f(x)=x^{2}$ tem valor mínimo global no ponto $x=0$ e não assume valor máximo global. A função $g(x)=-x^{2}$ tem valor máximo global no ponto $x=0$ e não assume valor mínimo global. A função $h(x)=x^{3}$ não assume valores mínimo e máximo globais. Veja a Figura 3.1.

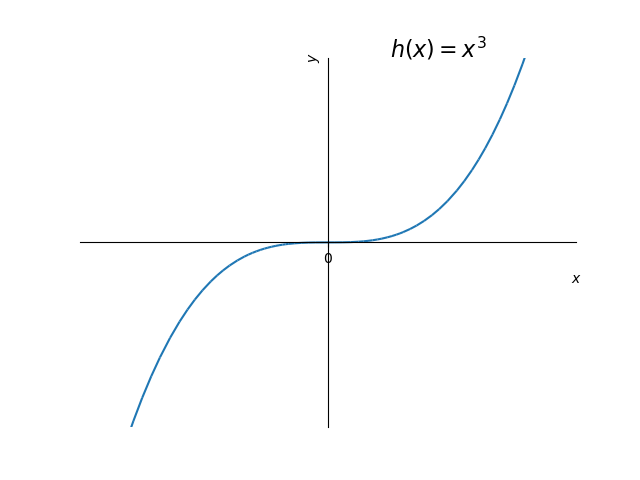
Refer to caption — Figura 3.1: Esboço das funções discutidas no Exemplo 3.2.1.

Teorema 3.2.1.

(Teorema do valor extremo²⁵²⁵endnote: ²⁵Este é uma versão do chamado Teorema de Weierstrass) Se $f$ é uma função contínua em um intervalo fechado $[a,b]$ , então $f$ assume tanto um valor máximo como um valor mínimo global em $[a,b]$ .

Demonstração.

A demonstração foge dos objetivos deste texto. Caso tenha interesse, consulte [2]. ∎

Exemplo 3.2.2.

Vejamos os seguintes casos:

a)

A função $\boldsymbol{f(x)=(x-1)^{2}+1}$ é contínua no intervalo fechado $\displaystyle\left[0,\frac{3}{2}\right]$ . Assume valor mínimo global $1$ no ponto $x=1$ . Ainda, assume valor máximo global igual a $2$ no ponto $x=0$ . Veja Figura 3.2.

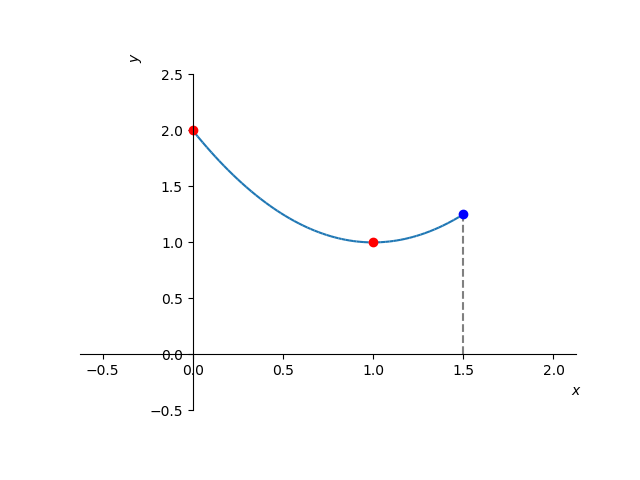
Figura 3.2: Esboço do gráfico de $f(x)=(x-1)^{2}+1$ no intervalo $\displaystyle\left[0,\frac{3}{2}\right]$ . Veja o Exemplo 3.2.2 a).
b)

A função $\boldsymbol{g(x)=\ln x}$ é contínua no intervalo $(0,e]$ . Neste intervalo, assume valor máximo global no ponto $x=e$ , mas não assume valor mínimo global. Veja Figura 3.3.

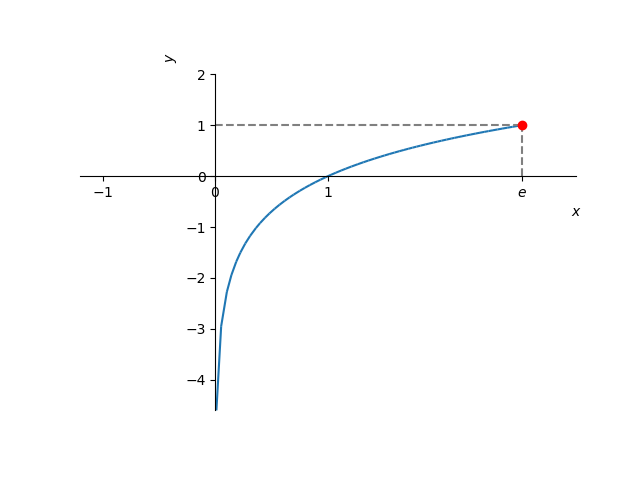
Figura 3.3: Esboço do gráfico de $g(x)=\ln x$ no intervalo $(0,e]$ . Veja o Exemplo 3.2.2 b).
c)

A função

$h(x)=\left\{\begin{array}[]{ll}x&,0\leq x<1,\\ 0&,x=1,\end{array}\right.$ (3.43)

definida no intervalo $[0,1]$ é descontínua no ponto $x=1$ . Neste intervalo, assume valor mínimo global no ponto $x=0$ , mas não assume valor máximo global. Veja a Figura 3.4.

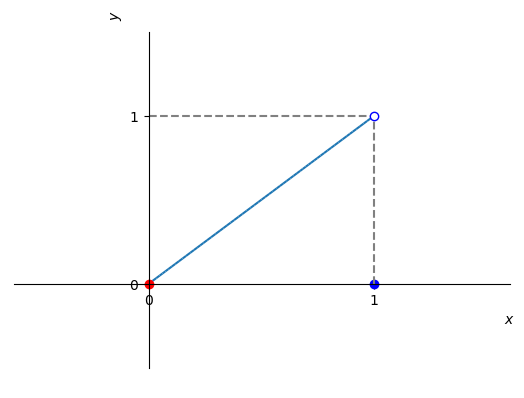
Figura 3.4: Esboço do gráfico de $h(x)$ no intervalo $[0,1]$ . Veja o Exemplo 3.2.2 c).

Uma função $f$ tem um valor máximo local em um ponto interior $x=a$ de seu domínio, se $f(x)<f(a)$ para todo $x$ em um intervalo aberto em torno de $a$ , excluindo-se $x=a$ . Analogamente, $f$ tem um valor mínimo local em um ponto interior $x=b$ de seu domínio, se $f(x)>f(b)$ para todo $x$ em um intervalo aberto em torno de $b$ , excluindo-se $x=b$ . Em tais pontos, dizemos que a função têm valores extremos locais (ou relativos). Um tal ponto é chamado de ponto de máximo local ou de mínimo local, conforme o caso.

Exemplo 3.2.3.

Consideremos a função

f(x)=\left\{\begin{array}[]{ll}-(x+1)^{2}-2&,-2\leq x<-\frac{1}{2},\\ |x|&,-\frac{1}{2}\leq x<1,\\ (x-2)^{3}+2&,1\leq x<3.\end{array}\right.

(3.44)

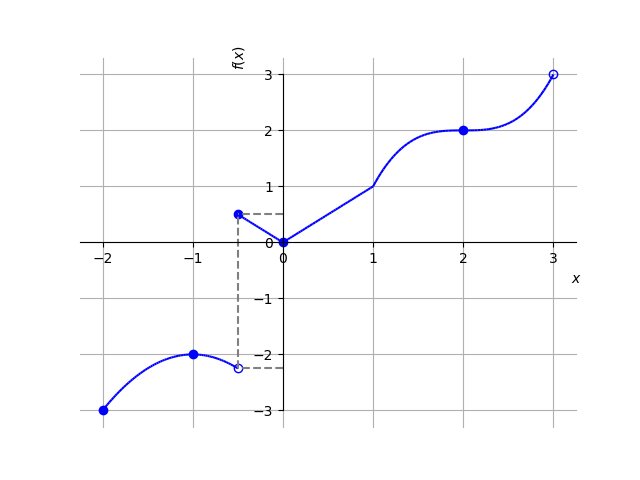
Na Figura 3.5 temos o esboço de seu gráfico. Por inferência, temos que $f$ tem valores máximos locais nos pontos $x=-1$ e $x=-1/2$ . No ponto $x=0$ tem um valor mínimo local. Observamos que $x=-2$ , $x=2$ e $x=3$ não são pontos de extremos locais desta função. No ponto $x=-2$ , $f$ tem seu valor mínimo global. Ainda, $f$ não tem valor máximo global.

Teorema 3.2.2.

(Teorema da derivada para pontos extremos locais.) Se $f$ possui um valor extremo local em um ponto $x=a$ e $f$ é diferenciável neste ponto, então

f^{\prime}(a)=0.

(3.45)

Demonstração.

Vamos considerar o caso em que $f$ possui um máximo local em $x=a$ . Então, segue que

	$\displaystyle f^{\prime}(a)=\lim_{h\to 0^{+}}\frac{f(x+h)-f(x)}{h}\leq 0$		(3.46)
	$\displaystyle f^{\prime}(a)=\lim_{h\to 0^{-}}\frac{f(x+h)-f(x)}{h}\geq 0$		(3.47)

Logo, $f^{\prime}(a)=0$ . Para o caso em que $f$ possui um mínimo local em $x=a$ , consulte o Exercício 3.2.6. ∎

Deste teorema, podemos concluir que uma função $f$ pode ter valores extremos em:

a)

pontos interiores de seu domínio onde $f^{\prime}=0$ ,
b)

pontos interiores de seu domínio onde $f^{\prime}$ não existe, ou
c)

pontos extremos de seu domínio.

Um ponto interior do domínio de uma função $f$ onde $f^{\prime}=0$ ou $f^{\prime}$ não existe, é chamado de ponto crítico da função.

Observação 3.2.1.

Uma função tem valores extremos em pontos críticos ou nos extremos de seu domínio.

Exemplo 3.2.4.

Consideramos a função $f(x)$ discutida no Exemplo 3.2.3. No ponto $x=-1$ , $f^{\prime}(-1)=0$ e $f$ tem valor máximo local neste ponto. Entretanto, no ponto $x=2$ , também temos $f^{\prime}(2)=0$ , mas $f$ não tem valor extremo neste ponto.

No ponto $x=0$ , $f^{\prime}(0)$ não existe e $f$ tem valor mínimo local neste ponto. No ponto, $x=-1/2$ , $f^{\prime}(1/2)$ não existe e $f$ tem valor máximo local neste ponto.

Nos extremos do domínio, temos que $f$ tem valor mínimo global no ponto $x=-2$ , mas não tem extremo global no ponto $x=3$ .

3.2.1 Exercícios resolvidos

ER 3.2.1.

Determine os pontos extremos da função $f(x)=(x+1)^{2}-1$ no intervalo $[-2,1]$ .

Solução.

Os valores extremos de um função podem ocorrer, somente, em seus pontos críticos ou nos extremos de seu domínio. Como $f(x)=(x+1)^{2}-1$ é diferenciável no intervalo $(-2,1)$ , seus pontos críticos são pontos tais que $f^{\prime}=0$ . Para identificá-los, calculamos

	$\displaystyle f^{\prime}(x)=0$	$\displaystyle\Rightarrow 2(x+1)=0$		(3.48)
		$\displaystyle\Rightarrow x=-1.$		(3.49)

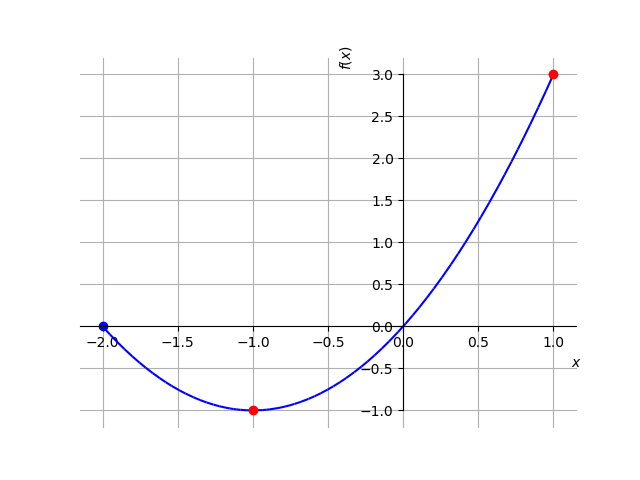
Desta forma, $f$ pode ter valores extremos nos ponto $x=-2$ , $x=-1$ e $x=1$ . Analisamos, então, o esboço do gráfico da função (Figura 3.6) e a seguinte tabela:

$x$	-2	-1	1
$f(x)$	0	-1	3

Daí, podemos concluir que $f$ tem o valor mínimo global (e local) de $f(-1)=-1$ no ponto $x=-1$ e tem valor máximo global de $f(1)=3$ no ponto $x=1$ .

Podemos usar o Python+SymPy para computar os pontos extremos e plotar a função. Por exemplo, com os seguintes comandos:

Código 61: Python

⬇

1import sympy as sp

2x = sp.Symbol('x')

3f = sp.lambdify(x, (x+1)**2-1)

4# f' == 0

5xc = sp.solve(sp.diff(f(x),x), x)

6print(f"Pto. crítico xc = {xc}")

7print(f"f(-2) = {f(-2)}")

8print(f"f({xc[0]}) = {f(xc[0])}")

9print(f"f(1) = {f(1)}")

10sp.plot(f(x), (x,-2,1))

ER 3.2.2.

Determine os pontos extremos da função $f(x)=x^{3}$ no intervalo $[-1,1]$ .

Solução.

Como $f$ é diferenciável no intervalo $(-1,1)$ , temos que seus pontos críticos são tais que $f^{\prime}(x)=0$ . Neste caso, temos

3x^{2}=0\Rightarrow x=0

(3.50)

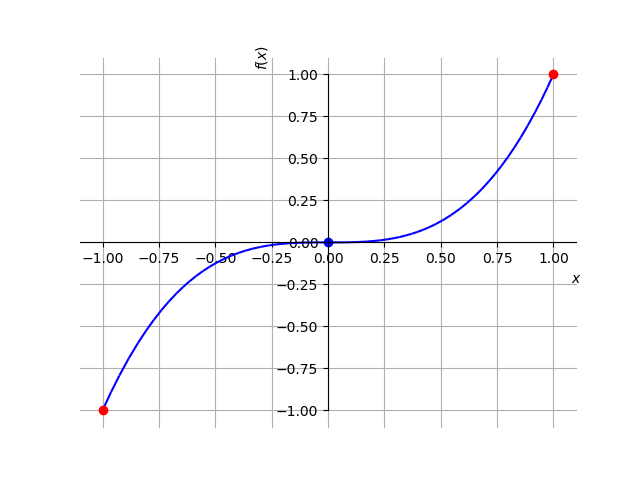
é o único ponto crítico de $f$ . Entretanto, analisando o gráfico desta função (Figura 3.7) vemos que $f$ não tem valor extremo local neste ponto. Assim, seus pontos extremos só podem ocorrer nos extremos do domínio $[-1,1]$ . Concluímos que $f(-1)=-1$ é o valor mínimo global de $f$ e $f(1)=1$ é seu valor máximo global.

3.2.2 Exercícios

E. 3.2.1.

Considere que uma dada função $f$ tenha o seguinte esboço de gráfico:

Determine e classifique os pontos extremos desta função.

Resposta.

$x=-1$ ponto de mínimo global; $x=1$ ponto de máximo local; $x=2$ ponto de mínimo local; $x=\frac{5}{2}$ ponto de máximo global.

E. 3.2.2.

Dada a função $f(x)=x^{2}-2x+3$ restrita ao intervalo $[-1,2]$ , determine:

a)

seu(s) ponto(s) crítico(s).
b)

seu(s) ponto(s) extremo(s) e o(s) classifique.
c)

seu(s) valor(es) extremo(s) e o(s) classifique.

Resposta.

a) $x=1$ ; b) $x=-1$ ponto de máximo global; $x=1$ ponto de mínimo local e global; c) $f(-1)=6$ valor máximo global; $f(1)=2$ valor mínimo local e global;

E. 3.2.3.

Dada a função $f(x)=-x^{2}+2x+1$ restrita ao intervalo $[0,3]$ , determine:

a)

seu(s) ponto(s) crítico(s).
b)

seu(s) ponto(s) extremo(s) e o(s) classifique.
c)

seu(s) valor(es) extremo(s) e o(s) classifique.

Resposta.

a) $x=1$ ; b) $x=1$ ponto de máximo local e global; $x=3$ ponto de mínimo global; c) $f(1)=2$ valor máximo local e global; $f(3)=-2$ valor mínimo global;

E. 3.2.4.

Dada a função $f(x)=x^{3}-3x^{2}+3x$ restrita ao intervalo $[0,\infty)$ , determine:

a)

seu(s) ponto(s) crítico(s).
b)

seu(s) ponto(s) extremo(s) e o(s) classifique.
c)

seu(s) valor(es) extremo(s) e o(s) classifique.

Resposta.

a) $x=1$ ; b) $x=0$ ponto de mínimo global;c) $f(0)=0$ valor mínimo global;

E. 3.2.5.

Dada a função $f(x)=x^{1/3}$ restrita ao intervalo $[-1,1]$ , determine:

a)

seu(s) ponto(s) crítico(s).
b)

seu(s) ponto(s) extremo(s) e o(s) classifique.
c)

seu(s) valor(es) extremo(s) e o(s) classifique.

Resposta.

a) $x=0$ ; b) $x=-1$ ponto de mínimo global; $x=1$ ponto de máximo global; c) $f(-1)=-1$ valor mínimo global; $f(1)=1$ valor máximo global;

E. 3.2.6.

Mostre que se $f$ tem um mínimo local em $x=a$ e é diferenciável neste ponto, então $f^{\prime}(a)=0$ .

Resposta.

Dica: consulte a demonstração do Teorema 3.2.2.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |