Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

2 Equação com Uma Incógnita 2.4 Método de Steffensen 2.6 Método da Secante

2.5 Método de Newton

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Seja $x^{*}$ um zero de uma dada função $f$ , i.e.

f(x^{*})=0.

(2.123)

A expansão em polinômio de Taylor²¹²¹endnote: ²¹Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor. de $f$ em um ponto $\tilde{x}$ dado, é

f(x^{*})=f(\tilde{x})+f^{\prime}(\tilde{x})(x^{*}-\tilde{x})+O\left(\left|x^{*% }-\tilde{x}\right|^{2}\right).

(2.124)

Como $f(x^{*})=0$ , temos

	$\displaystyle 0=f(\tilde{x})+f^{\prime}(\tilde{x})(x^{}-\tilde{x})+O\left(% \left\|x^{}-\tilde{x}\right\|^{2}\right)$		(2.125)
	$\displaystyle x^{}=\tilde{x}-\frac{f(\tilde{x})}{f^{\prime}(\tilde{x})}+O% \left(\left\|x^{}-\tilde{x}\right\|^{2}\right)$		(2.126)

Esta última expressão nos indica que dada uma aproximação $\tilde{x}$ do zero de $f$ a expressão

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\tilde{x}-% \frac{f(\tilde{x})}{f^{\prime}(\tilde{x})},

(2.127)

aproxima $x^{*}$ com um erro da ordem de $|x^{*}-\tilde{x}|^{2}$ .

Estas observações nos levam a iteração de Newton²²²²endnote: ²²Sir Isaac Newton, matemático e físico inglês, 1642 - 1726/27. Fonte: Wikipedia.

	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x^{(0)}$	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}=\text{aprox. % inicial},$		(2.128)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x^{(k+1)}$	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}=x^{(k)}-\frac% {f(x^{(k)})}{f^{\prime}(x^{(k)})},$		(2.129)

com $k=0,1,2,\ldots$ .

Exemplo 2.5.1.

Consideramos o problema de encontrar o zero da função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.130)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.130)

no intervalo $[2,3]$ (Consulte a Figura 2.8).

Refer to caption — Figura 2.8: Função $f$ do Exemplo 2.5.1.

Fazendo as iterações de Newton com aproximação inicial $x^{(0)}=2.6$ , obtemos os resultados apresentados na Tabela 2.6.

Tabela 2.6: Resultados referentes ao Exemplo 2.5.1.

$k$	$x^{(k)}$	$\|x^{(k)}-x^{(k-1)}\|$
0	$2.6000$	-x-
1	$2.3836$	$2.2\mathrm{e}\!-\!1$
2	$2.3566$	$2.7\mathrm{e}\!-\!2$
3	$2.3562$	$3.9\mathrm{e}\!-\!4$
4	$2.3562$	$8.3\mathrm{e}\!-\!8$

⬇

1import numpy as np

3# fun obj

4f = lambda x: np.sin(x+np.pi/4)**2 \

5 - x**3 + np.pi/4*x**2 + 5*np.pi**2/16*x \

6 + 3*np.pi**3/64

8fl = lambda x: 2*np.sin(x+np.pi/4)*np.cos(x+np.pi/4) \

9 -3*x**2 + np.pi/2*x + 5*np.pi**2/16

11# aprox. inicial

12x0 = 2.6

13print(f'0: {x0:.4e}')

15# iterações

16for k in range(4):

17 x = x0 - f(x0)/fl(x0)

18 print(f'{k+1}: {x:.4e}')

19 x0 = x

Observação 2.5.1.

O método de Newton é uma iteração de ponto fixo ótima. Do Teorema do Ponto Fixo (Teorema 2.3.1), a iteração

	$\displaystyle x^{k+1}$	$\displaystyle=g(x^{(k)})$		(2.131)
		$\displaystyle:=x^{(k)}-\alpha f(x)$		(2.132)

tem taxa de convergência²³²³endnote: ²³Supondo verdadeiras as demais hipóteses do Teorema 2.3.1.

|x^{(k+1)}-x^{(k)}|\leq K|x^{(k)}-x^{(k-1)}|,

(2.133)

com $K$ tal que $|g^{\prime}(x)|=|1-\alpha f^{\prime}(x)|<K<1$ . Isto nos indica que a melhor escolha para $\alpha$ é

\alpha=\frac{1}{f^{\prime}(x)},

(2.134)

de forma que (2.132) coincide com a iteração de (2.129).

2.5.1 Interpretação Geométrica

Dadas uma aproximação $x^{(k)}$ de um zero de uma função $f$ , a iteração de Newton fornece uma nova aproximação $x^{(k+1)}$ com

x^{(k+1)}=x^{(k)}-\frac{f(x^{(k)})}{f^{\prime}(x^{(k)})}.

(2.135)

Subtraindo $x^{(k+1)}$ e multiplicando por $-f^{\prime}(x^{(k)})$ , obtemos

0=f^{\prime}(x^{(k)})(x^{(k+1)}-x^{(k)})+f(x^{(k)}),

(2.136)

Observemos que o lado direito desta última equação corresponde a expressão da reta tangente ao gráfico de $f$ pelo ponto $(x^{(k)},f(x^{(k)}))$ , avaliada em $x^{(k+1)}$ . Mais precisamente, a equação desta reta tangente é

y=f^{\prime}(x^{(k)})(x-x^{(k)})+f(x^{(k)})

(2.137)

e a equação (2.136) nos informa que em $x=x^{(k+1)}$ a reta tangente cruza o eixo $x$ .

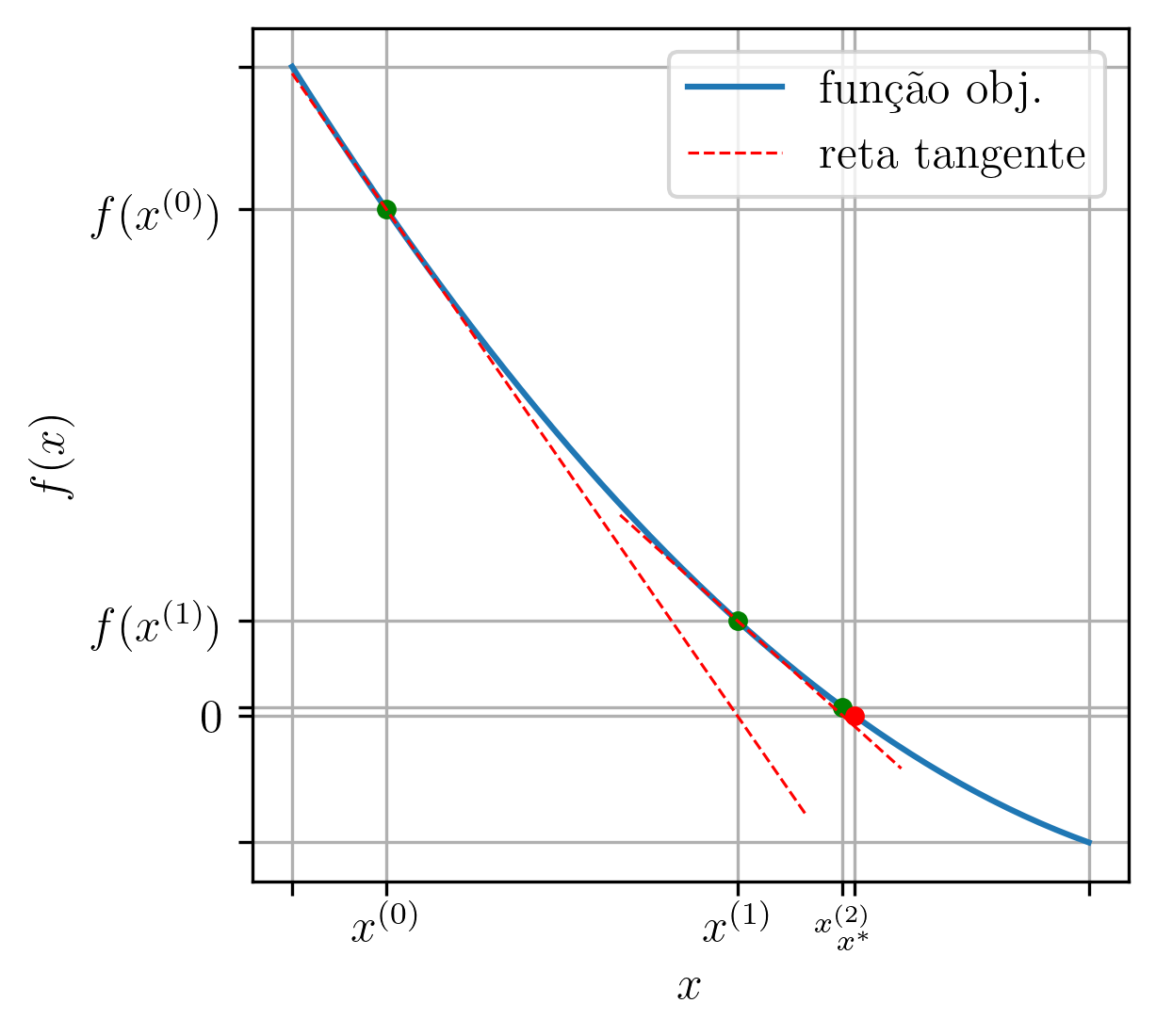
Destas observações, concluímos que a iterada $x^{(k+1)}$ do método de Newton corresponde ao ponto de interseção da reta tangente ao gráfico da $f$ pelo ponto $(x^{k},f(x^{k}))$ com o eixo das abscissas²⁴²⁴endnote: ²⁴Eixo $x$ .. Consulte a Figura 2.9.

Exemplo 2.5.2.

Consideremos que o método de Newton seja usado para aproximarmos o zero de

f(x)=(x-1)e^{-x^{2}}.

(2.138)

Observemos que esta função tem $x=1$ como seu único zero. Agora, se escolhermos $x^{(0)}=0.5$ as iterações de Newton convergem para este zero, mas, se escolhermos $\tilde{x}^{(0)}=1.5$ não (consulte a Tabela 2.7).

Tabela 2.7: Resultados referentes ao Exemplo 2.5.2

$k$	$x^{(k)}$	$\tilde{x}^{(k)}$
0	$5.0000\mathrm{e}\!-\!1$	$1.5000\mathrm{e}\!+\!0$
1	$8.3333\mathrm{e}\!-\!1$	$2.5000\mathrm{e}\!+\!0$
2	$9.6377\mathrm{e}\!-\!1$	$2.7308\mathrm{e}\!+\!0$
3	$9.9763\mathrm{e}\!-\!1$	$2.9355\mathrm{e}\!+\!0$
4	$9.9999\mathrm{e}\!-\!1$	$3.1223\mathrm{e}\!+\!0$
5	$1.0000\mathrm{e}\!+\!0$	$3.2955\mathrm{e}\!+\!0$

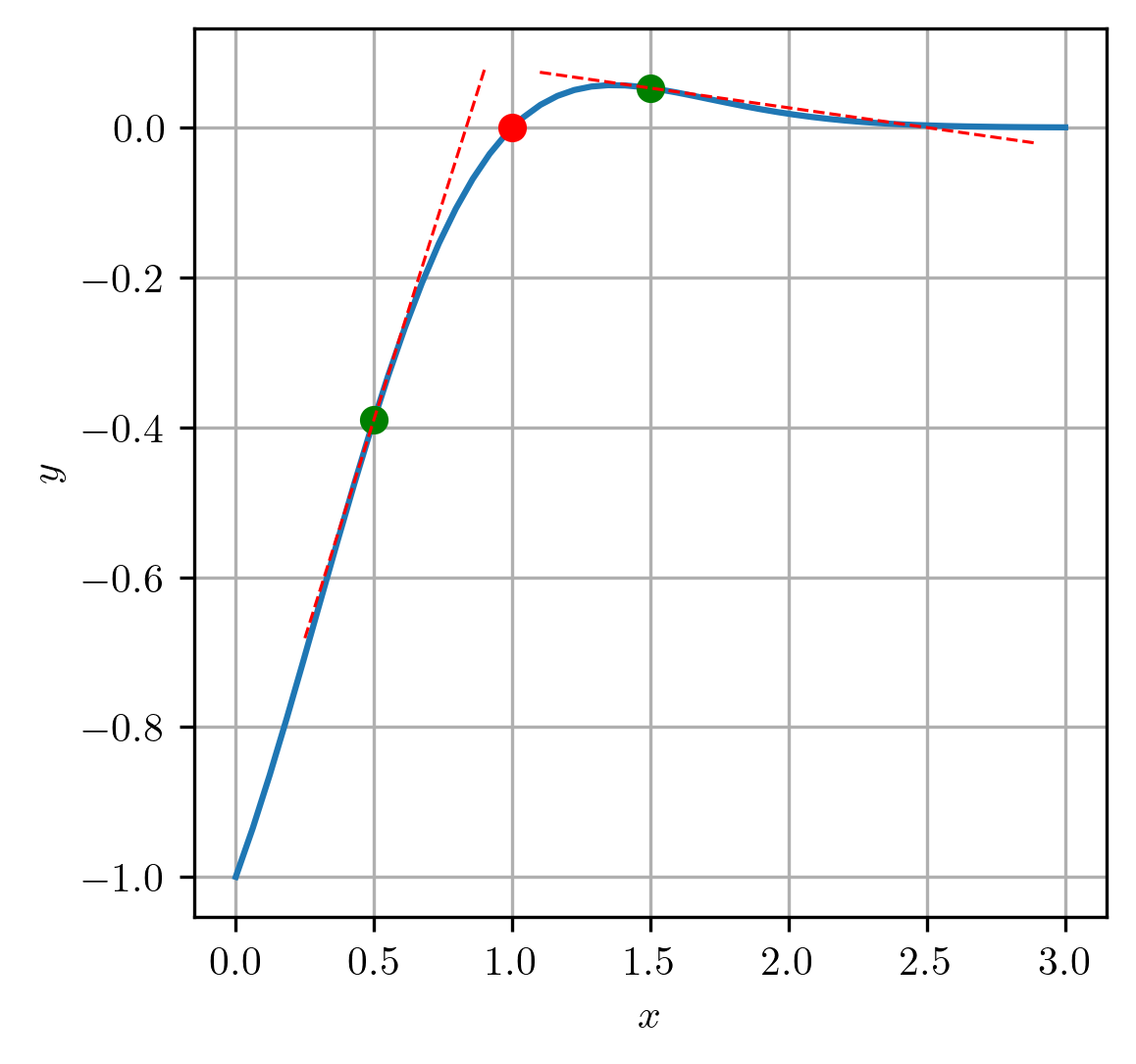
Embora ambas aproximações iniciais estão a mesma distância da solução $x=1$ , quando tomamos $x^{(0)}=1.5$ as iterações irão divergir, como podemos observar da interpretação geométrica dada na Figura 2.10.

2.5.2 Análise de Convergência

Seja $x^{*}$ o zero de uma dada função $f$ duas vezes continuamente diferenciável com $f^{\prime}(x)\neq 0$ para todo $x\in[x^{*}-\varepsilon_{0},x^{*}+\varepsilon_{0}]$ para algum $\varepsilon_{0}>0$ . Seja, também, $(x^{(k)})_{k=0}^{\infty}$ a sequência das iteradas de Newton

x^{(k+1)}=x^{(k)}-\frac{f(x^{(k)})}{f^{\prime}(x^{(k)})},\quad k=0,1,2,\ldots,

(2.139)

com aproximação inicial $x^{(0)}\in(x^{*}-\varepsilon_{0},x^{*}+\varepsilon_{0})$ . Então, do polinômio de Taylor de grau 1 de $f$ em torno de $x^{(0)}$ , temos

f(x^{*})=f(x^{(0)})+f^{\prime}(x^{(0)})(x^{*}-x^{(0)})+\frac{f^{\prime\prime}(% \xi^{(0)})}{2!}(x^{*}-x^{(0)})^{2},

(2.140)

onde $\xi^{(0)}$ está entre $x^{(0)}$ e $\xi^{(0)}$ . Daí, rearranjamos os termos e notamos que $f(x^{*})=0$ para obtermos

x^{*}-\left[x^{(0)}-\frac{f(x^{(0)})}{f^{\prime}(x^{(0)})}\right]=\frac{f^{% \prime\prime}(\xi^{(0)})}{2f^{\prime}(x^{(0)})}(x^{*}-x^{(0)})^{2}.

(2.141)

Então, da iteração de Newton (2.139), temos

x^{*}-x^{(1)}=\frac{f^{\prime\prime}(\xi^{(0)})}{2f^{\prime}(x^{(0)})}(x^{*}-x% ^{(0)})^{2}

(2.142)

Logo,

|x^{*}-x^{(1)}|\leq C|x^{*}-x^{(0)}|^{2},

(2.143)

com

C=\sup_{x,y\in[x^{*}-\varepsilon,x^{*}+\varepsilon]}\left|\frac{f^{\prime% \prime}(x)}{2f^{\prime}(y)}\right|.

(2.144)

Segue, então, que se $x^{(0)}\in(x^{*}-\varepsilon,x^{*}+\varepsilon)$ para algum $\varepsilon>0$ tal que

C|x^{*}-x^{(0)}|^{2}<1,\quad\forall x\in(x^{*}-\varepsilon,x^{*}+\varepsilon),

(2.145)

então $x^{(1)}\in(x^{*}-\varepsilon,x^{*}+\varepsilon)$ .

Logo, por indução matemática²⁵²⁵endnote: ²⁵Veja o exercício 2.5.6., temos que o método de Newton tem ordem de convergência quadrática

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}|x^{(k+1)}-x^{% *}|\leq C|x^{(k)}-x^{*}|^{\boldsymbol{2}},

(2.146)

para qualquer escolha de $x^{(0)}$ suficientemente próximo de $x^{*}$ , i.e. $x^{(0)}\in(x^{*}-\varepsilon,x^{*}+\varepsilon)$ .

Observação 2.5.2.

O intervalo $(x^{*}-\varepsilon,x^{*}+\varepsilon)$ é chamado de bacia de atração do método de Newton.

Exemplo 2.5.3.

Retornamos ao problema de encontrar o zero da função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.147)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.147)

no intervalo $[2,3]$ . Este problema foi construído de forma que $x^{*}=3\pi/4$ é um zero de $f$ . Então, fazendo as iterações de Newton com aproximação inicial $x^{(0)}=2.6$ , obtemos os resultados apresentados na Tabela 2.8, os quais evidenciam a convergência quadrática das iterações computadas.

Tabela 2.8: Resultados referentes ao Exemplo 2.5.3.

$k$	$x^{(k)}$	$\|x^{(k)}-x^{*}\|$
0	$2.6000$	$2.4\mathrm{e}\!-\!01$
1	$2.3836$	$2.7\mathrm{e}\!-\!02$
2	$2.3566$	$3.9\mathrm{e}\!-\!04$
3	$2.3562$	$8.3\mathrm{e}\!-\!08$
4	$2.3562$	$3.6\mathrm{e}\!-\!15$

2.5.3 Zeros Múltiplos

Na análise de convergência acima foi necessário assumir que $f^{\prime}(x)\neq 0$ para todo $x$ em uma vizinha do zero $x^{*}$ da função $f$ . Isto não é possível no caso de $x^{*}$ ser um zero duplo pois, então, $f^{\prime}(x^{*})=0$ . Neste caso, podemos aplicar o método de Newton a $f^{\prime}(x)$ , a qual tem $x^{*}$ como um zero simples.

Exemplo 2.5.4.

Consideremos o problema de aproximar o zero da função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.148)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.148)

no intervalo $[-1.0]$ . Este problema foi construído de forma que $x^{*}=-\pi/4$ é um zero duplo de $f$ . Então, aplicamos o método de Newton a

	$\displaystyle f^{\prime}(x)$	$\displaystyle=2\operatorname{sen}\left(x+\frac{\pi}{4}\right)\cos\left(x+\frac% {\pi}{4}\right)$		(2.149)
		$\displaystyle-3x²+\frac{\pi}{2}x+\frac{5\pi^{2}}{16}.$		(2.149)

Ou seja, as iterações de Newton são

x^{(k+1)}=x^{(k)}-\frac{f^{\prime}(x^{(k)})}{f^{\prime\prime}(x^{(k)})},\quad k% =0,1,2,\ldots,

(2.150)

sendo $x^{(1)}$ uma aproximação inicial. Na Tabela 2.9, temos os resultados obtidos da computação destas iterações com $x^{(1)}=-0.5$ .

Tabela 2.9: Resultados referentes ao Exemplo LABEL:cap_eq1d_sec_newton:ex:Newton_multpar.

$k$	$x^{(k)}$	$\|x^{(k)}-x^{*}\|$
0	-0.5000
1	-0.8341	3.3e-01
2	-0.7862	4.8e-02
3	-0.7854	7.9e-04
4	-0.7854	2.3e-07
5	-0.7854	1.9e-14

Observação 2.5.3.

(Zeros múltiplos.) No caso de zeros de multiplicidade $m>1$ de uma dada função $f$ , podemos aplicar o método de Newton à derivada $m-1$ de $f$ , o que requer o cálculo de $m$ derivadas de $f$ . Alternativamente, consideramos aplicar o método à função auxiliar

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\mu(x):=\frac{% f(x)}{f^{\prime}(x)}.

(2.151)

De fato, se $x^{*}$ é zero de multiplicidade $m\geq 1$ de $f$ , então existe uma função $g$ tal que $g(x^{*})\neq 0$ e

f(x)=\left(x-x^{*}\right)^{m}g(x)

(2.152)

Com isso, temos

	$\displaystyle\mu(x)$	$\displaystyle=\frac{\left(x-x^{}\right)^{m}g(x)}{m\left(x-x^{}\right)^{m-1}g% (x)+\left(x-x^{*}\right)^{m}g^{\prime}(x)}$
		$\displaystyle=\frac{\left(x-x^{}\right)g(x)}{mg(x)+\left(x-x^{}\right)g^{% \prime}(x)}$

Como $g\left(x^{*}\right)\neq 0$ , temos que

\frac{g(x^{*})}{mg\left(x^{*}\right)+\left(x^{*}-x^{*}\right)g^{\prime}\left(x% ^{*}\right)}=\frac{1}{m}\neq 0.

(2.153)

Ou seja, $x^{*}$ é um zero simples de $\mu$ . A iteração do Método de Newton aplicado à $\mu$ fornece

	$\displaystyle x^{(k+1)}$	$\displaystyle=x^{(k)}-\frac{\mu\left(x^{(k)}\right)}{\mu^{\prime}\left(x^{k+1}% \right)}$		(2.154)
		$\displaystyle=x^{(k)}=\frac{\frac{f\left(x^{(k)}\right)}{f^{\prime}\left(x^{(k% )}\right)}}{\frac{\left[f^{\prime}\left(x^{(k)}\right)\right]^{2}-f\left(x^{(k% )}\right)f^{\prime\prime}\left(x^{(k)}\right)}{\left[f^{\prime}\left(x^{(k)}% \right)\right]^{2}}}$		(2.155)

Rearranjando os termos, obtemos a iteração modificada de Newton para zeros de multiplicidade maior que 1

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x^{(k+1)}=x^{(% k)}-\frac{f\left(x^{(k)}\right)f^{\prime}\left(x^{(k)}\right)}{\left[f^{\prime% }\left(x^{(k)}\right)\right]^{2}-f\left(x^{(k)}\right)f^{\prime\prime}\left(x^% {(k)}\right)}.

(2.156)

Para uma aplicação, consulte o exercício 2.5.3.

Exercícios

E. 2.5.1.

Use o método de Newton para obter uma aproximação do zero de $f(x)=x^{3}\operatorname{sen}(x)-\cos(x)$ no intervalo $[0.5,1]$ com precisão de $10^{-6}$ .

Resposta.

$9.15811\times 10^{-1}$

E. 2.5.2.

Use o método de Newton para obter uma aproximação do zero de

	$\displaystyle f(x)$	$\displaystyle=(-x^{2}+1.154x-0.332929)\cos(x)$		(2.157)
		$\displaystyle+x^{2}-1.154x+0.332929$		(2.157)

no intervalo $(0.55,0.65)$ com precisão de $10^{-5}$ .

Resposta.

$5.7700\times 10^{-1}$

E. 2.5.3.

A função (2.148) tem um zero de multiplicidade par em $x=-\pi/4$ . Assumindo a aproximação inicial $x^{(0)}=-0.5$ , aplique a iteração modificada de Newton dada em (2.156) e compare os resultados com apresentados na Tabela 2.9.

E. 2.5.4.

Assumindo a aproximação inicial $x^{(0)}=1$ , aproxime o zero de

f(x)=e^{x}-x-1

(2.158)

usando:

a)

a iteração de Newton para $f$ .
b)

a iteração de Newton para $f^{\prime}$ .
c)

a iteração modificada de Newton²⁶²⁶endnote: ²⁶Equação (2.156). para $f$ .

Qual a melhor abordagem? Justifique sua resposta.

Resposta.

Dica: Analise a convergência das iteradas para cada abordagem.

E. 2.5.5.

Use o Método de Newton para obter a aproximação do zero de

p(x)=x^{3}-3\pi x^{2}+3\pi^{2}x-\pi^{3}.

(2.159)

Resposta.

Dica: $x=\pi$ é zero de multiplicidade 3.

Análise Numérica

E. 2.5.6.

Complete a demonstração por indução matemática de que o método de Newton tem taxa de convergência quadrática.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |