Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

2 Equação com Uma Incógnita 2.5 Método de Newton 2.7 Raízes de Polinômios

2.6 Método da Secante

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

O Método da Secante é um método tipo de Newton. Observamos que para duas aproximações $x^{(k)}$ e $x^{(k-1)}$ suficientemente próximas, temos²⁷²⁷endnote: ²⁷Razão fundamental do Cálculo.

f^{\prime}(x^{(k)})\approx\frac{f(x^{(k)})-f(x^{(k-1)})}{x^{(k)}-x^{(k-1)}}.

(2.160)

Assim sendo, substituindo esta aproximação na iteração de Newton (Eq. (2.129)), obtemos a iteração do Método da Secante

	$\displaystyle x^{(0)}$	$\displaystyle,x^{(1)}=\text{aprox. iniciais},$		(2.161a)
	$\displaystyle x^{(k+1)}$	$\displaystyle=x^{(k)}-f(x^{(k)})\frac{x^{(k)}-x^{(k-1)}}{f(x^{(k)})-f(x^{(k-1)% })},$		(2.161b)

para $k=1,2,3,\ldots$ .

Exemplo 2.6.1.

Consideramos o problema de encontrar o zero da função

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.162)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.162)

no intervalo $[2,3]$ . Fazendo as iterações do Método da Secante com aproximações iniciais $x^{(0)}=2.6$ e $x^{(1)}=2.5$ , obtemos os resultados apresentados na Tabela 2.10.

Tabela 2.10: Resultados referentes ao Exemplo LABEL:cap_eq1d_sec_secante:ex:secante_exec.

$k$	$x^{(k-1)}$	$x^{(k)}$	$\|x^{(k)}-x^{(k-1)}\|$
0	$2.6000$	$2.5000$	-x-
1	$2.5000$	$2.3728$	$1.3\mathrm{e}\!-\!1$
2	$2.3728$	$2.3574$	$1.5\mathrm{e}\!-\!2$
3	$2.3574$	$2.3562$	$1.2\mathrm{e}\!-\!3$
4	$2.3562$	$2.3562$	$1.1\mathrm{e}\!-\!5$
5	$2.3562$	$2.3562$	$7.0\mathrm{e}\!-\!9$

⬇

1import numpy as np

3# fun obj

4f = lambda x: np.sin(x+np.pi/4)**2 \

5 - x**3 + np.pi/4*x**2 + 5*np.pi**2/16*x \

6 + 3*np.pi**3/64

8# aprox. iniciais

9x0 = 2.6

10x1 = 2.5

11print(f'\n0: {x0:.4f}, {x1:.4f}')

13# iterações

14for k in range(5):

15 x = x1 - f(x1)*(x1-x0)/(f(x1)-f(x0))

16 x0 = x1

17 x1 = x

18 print(f'{k+1}: {x0:.4f}, {x1:.4f}, {np.fabs(x1-x0):.1e}')

2.6.1 Interpretação Geométrica

A iteração do Método da Secante é

x^{(k+1)}=x^{(k)}-f(x^{(k)})\frac{x^{(k)}-x^{(k-1)}}{f(x^{(k)})-f(x^{(k-1)})},

(2.163)

donde segue que

0=x^{(k+1)}-x^{(k)}+f(x^{(k)})\frac{x^{(k)}-x^{(k-1)}}{f(x^{(k)})-f(x^{(k-1)})},

(2.164)

bem como que

0=\frac{f(x^{(k)})-f(x^{(k-1)})}{x^{(k)}-x^{(k-1)}}(x^{(k+1)}-x^{(k)})+f(x^{(k% )}).

(2.165)

Ou seja, $x^{(k+1)}$ é o ponto de interseção da reta

y=\frac{f(x^{(k)})-f(x^{(k-1)})}{x-x^{(k-1)}}(x^{(k+1)}-x^{(k)})+f(x^{(k)}).

(2.166)

com o eixo $x$ . Esta é a reta secante ao gráfico de $f$ pelos pontos $(x^{(k)},f(x^{(k)}))$ e $(x^{(k-1)},f(x^{(k-1)}))$ .

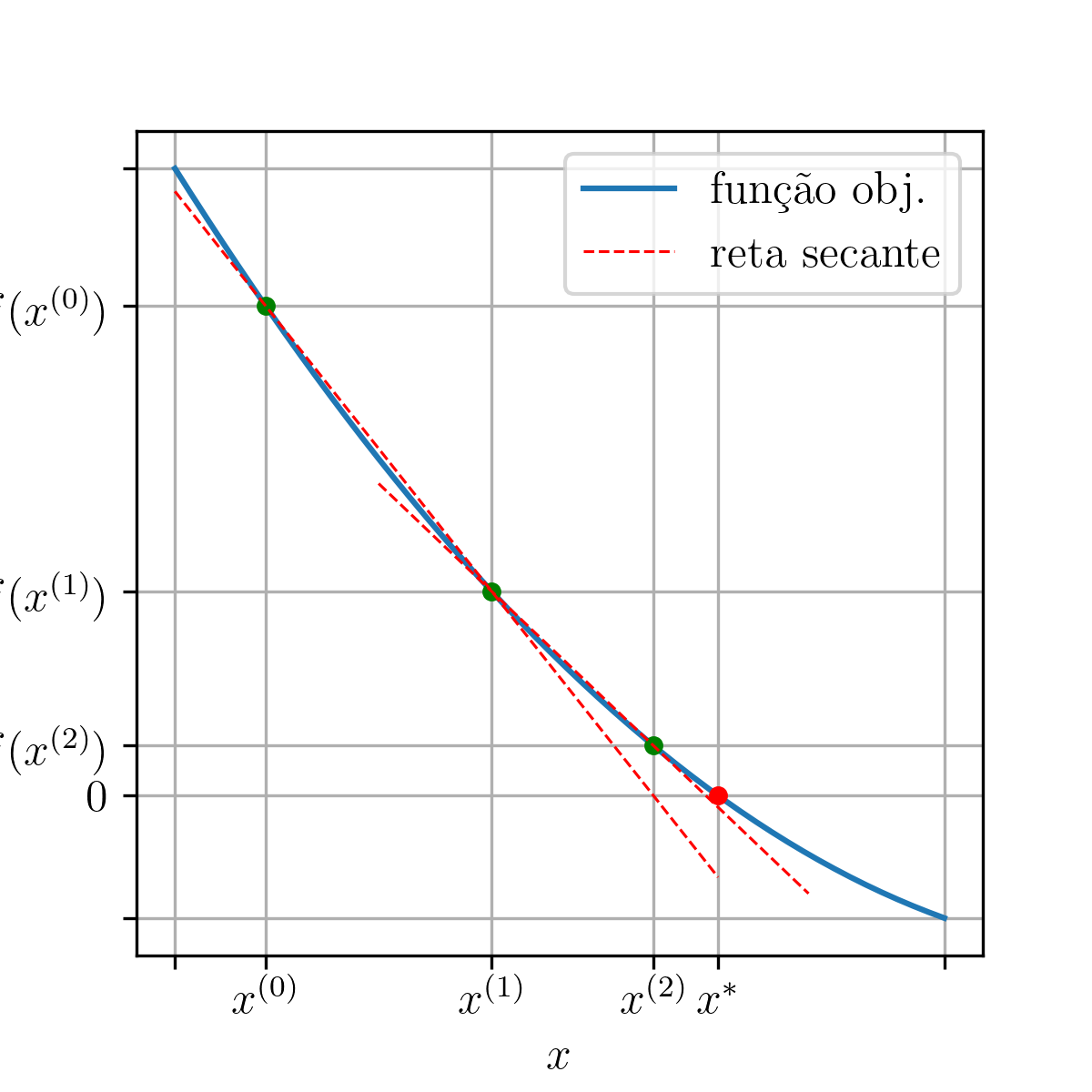
Refer to caption — Figura 2.11: Interpretação geométrica do Método da Secante.

Observação 2.6.1.

(Aproximações iniciais.) A interpretação geométrica do método da secante pode nos ajudar a escolher as aproximações iniciais $x^{(1)}$ e $x^{(2)}$ . Como uma boa prática, escolhemo-las próximas do zero (por inspeção gráfica), tomando $x^{(1)}$ como uma aproximação melhor que $x^{(0)}$ .

Observação 2.6.2.

(Ordem de convergência super-linear.) A ordem de convergência do Método da Secante é superlinear com

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}|x^{(k+1)}-x^{% *}|\leq C|x^{(k)}-x^{*}|^{\boldsymbol{\varphi}},

(2.167)

onde $\varphi=(1+\sqrt{5})/2\approx 1.618$ (razão áurea) e $x^{*}$ é o zero de $f$ .

Observação 2.6.3.

(Zeros de multiplicidade par.) A ordem de convergência super-linear do método da secante não se mantém para o caso de $x^{*}$ ser um zero múltiplo. Para contornar este problema, pode-se aplicar o método à derivada $n-1$ de $f$ , a fim de se aproximar um zero de multiplicidade $n$ .

Observação 2.6.4.

(Cancelamento catastrófico.) Conforme convergem as iterações do método da secante, o denominador $f(x^{(k)})-f(x^{(k-1)})$ pode convergir rapidamente para zero, ocasionando uma divisão por zero.

Exercícios

E. 2.6.1.

Use o Método da Secante para obter uma aproximação do zero de

f(x)=x^{3}\operatorname{sen}(x)-\cos(x)

(2.168)

no intervalo $[0.5,1]$ com precisão de $10^{-5}$ .

Resposta.

$9.1581\times 10^{-1}$

E. 2.6.2.

Use o Método da Secante para computar a(s) solução(ões) das seguintes equações com precisão de 8 dígitos significativos.

a)

$x=2^{-x}$ para $0\leq x\leq 2$ .
b)

$e^{-x^{2}}=3x-x^{2}$ para $-1\leq x\leq 4$ .

Resposta.

a) $6.4118574\times 10^{-1}$ ; b) $3.3536470\times 10^{-1}$ ; $2.9999589$

E. 2.6.3.

Use o Método da Secante para obter uma aproximação do zero de

	$\displaystyle f(x)$	$\displaystyle=\operatorname{sen}^{2}\left(x+\frac{\pi}{4}\right)-x^{3}$		(2.169)
		$\displaystyle+\frac{\pi}{4}x^{2}+\frac{5\pi^{2}}{16}x+\frac{3\pi^{3}}{64}.$		(2.169)

no intervalo $[-1,0]$ com precisão de $10^{-}5$ . Compare a convergência entre as seguintes abordagens:

a)

aplicando a iteração (2.6) diretamente à $f$ .
b)

aplicando a iteração (2.6) diretamente à $f^{\prime}$ .

Qual das duas abordagens tem convergência mais rápida? Justifique sua resposta.

Resposta.

Dica: $f$ tem um zero de multiplicidade par no intervalo $[-1,0]$ .

E. 2.6.4.

Use o Sétodo da Secante para obter uma aproximação do zero de

	$\displaystyle f(x)$	$\displaystyle=(-x^{2}+1.154x-0.332929)\cos(x)$		(2.170)
		$\displaystyle+x^{2}-1.154x+0.332929$		(2.170)

no intervalo $[0.55,0.65]$ com precisão de $10^{-}5$ .

Resposta.

$5.7700\times 10^{-1}$

E. 2.6.5.

Use o Método da Secante para encontrar uma aproximação com precisão de $4$ dígitos significativos do zero de

	$\displaystyle f(x)$	$\displaystyle=(-x^{2}+1.154x-0.332929)\cos(x)+x^{2}$		(2.171)
		$\displaystyle-1.154x+0.332929$		(2.171)

no intervalo $[-1,0]$ .

Resposta.

$-7.861\times 10^{-1}$

bootstra

E. 2.6.6.

Use o Método da Secante para encontrar o ponto crítico²⁸²⁸endnote: ²⁸Definimos que $x$ é ponto crítico de uma dada $f$ , quando $f^{\prime}(x)=0$ ou $\nexists f^{\prime}(x)$ . de

f(x)=(1-x^{2})e^{-x^{2}}

(2.172)

no intervalo $[0,2]$ . Obtenha o resultado com precisão de $5$ dígitos significativos por arredondamento.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |