Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

5 EDO linear de ordem mais alta com coeficientes variáveis 5.1 EDO de ordem 2 com coeficientes variáveis: fundamentos 5.3 Equação de Bessel

5.2 Integrais de Euler

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Nesta seção, vamos estudar as integrais de Euler de primeiro tipo (ou, função beta) e a de segundo tipo (ou, função gama).

5.2.1 Função gama

Assista no YouTube

Assista no archive.org!

Escute a audioleitura!

A função gama (ou integral de Euler de segundo tipo) é definida por

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\Gamma(x)=\int% _{0}^{\infty}z^{x-1}e^{-z}\,dz},

(5.116)

para qualquer $x$ número real positivo.

Ela pode ser interpretada como a generalização para números reais da função fatorial de números naturais. Isto se deve ao fato de que

	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1% }\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\Gamma(n+1)}$	$\displaystyle={\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{% 0,0,1}\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}n!}$		(5.117)
		$\displaystyle=n\cdot(n-1)\cdot(n-2)\cdot\,\cdots\,\cdot 1$		(5.118)

para qualquer $n$ número natural²⁷²⁷endnote: ²⁷Por definição, $0!=1$ ..

De fato, temos ${\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\Gamma(1)=1}$ , pois da definição (5.116) temos

$\displaystyle\Gamma(1)$	$\displaystyle=\int_{0}^{\infty}z^{1-1}e^{-z}\,dz$	(5.119)
	$\displaystyle=\int_{0}^{\infty}e^{-z}\,dz$	(5.120)
	$\displaystyle=\left.-e^{-z}\right\|_{0}^{\infty}$	(5.121)
	$\displaystyle=\lim_{z\to\infty}\cancelto{0}{\left(-e^{-z}\right)}-\lim_{z\to 0% }\cancelto{-1}{\left(-e^{-z}\right)}$	(5.122)
	$\displaystyle=1.$	(5.123)

Além disso, vale a propriedade

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\Gamma(x+1)=x% \Gamma(x)}.

(5.124)

De fato, da definição (5.116) e por integração por partes, temos

$\displaystyle\Gamma(x+1)$	$\displaystyle=\int_{0}^{\infty}z^{x+1-1}e^{-z}\,dz$	(5.125)
	$\displaystyle=\int_{0}^{\infty}\underbrace{z^{x}}_{u}\cdot\underbrace{e^{-z}\,% dz}_{dv}$	(5.126)
	$\displaystyle=\cancelto{0}{\left.\underbrace{z^{x}}_{u}\cdot\underbrace{\left(% -e^{-z}\right)}_{v}\right\|_{z=0}^{\infty}}-\int_{0}^{\infty}\underbrace{-e^{-z% }}_{v}\cdot\underbrace{xz^{x-1}\,dz}_{du}$	(5.127)
	$\displaystyle=x\int_{0}^{\infty}z^{x-1}e^{-z}\,dz$	(5.128)
	$\displaystyle=x\Gamma(x).$	(5.129)

Logo, para $n$ número natural, temos

$\displaystyle\Gamma(n+1)$	$\displaystyle=n\Gamma(n)$	(5.130)
	$\displaystyle=n\cdot(n-1)\Gamma(n-1)$	(5.131)
	$\displaystyle=n\cdot(n-1)\cdot(n-2)\Gamma(n-2)$	(5.132)
	$\displaystyle\vdots$	(5.133)
	$\displaystyle=n\cdot(n-1)\cdot(n-2)\cdot\,\cdots\,\cdot 1\Gamma(1)$	(5.134)
	$\displaystyle=n\cdot(n-1)\cdot(n-2)\cdot\,\cdots\,\cdot 1$	(5.135)
	$\displaystyle=n!$	(5.136)

Exemplo 5.2.1.

$\displaystyle\Gamma(5)$	$\displaystyle=4!$	(5.137)
	$\displaystyle=4\cdot 3\cdot 2\cdot 1$	(5.138)
	$\displaystyle=24.$	(5.139)

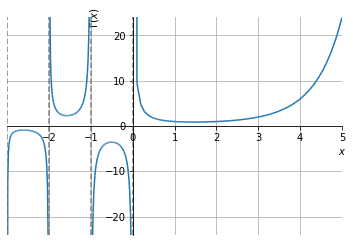
Refer to caption — Figura 5.1: Esboço do gráfico da função gama $\Gamma(x)$ .

Observação 5.2.1.

Vejamos as seguintes observações:

a)

$\nexists\Gamma(0)$

De fato, $\Gamma(0)$ não está definido pois

$\lim_{x\to 0^{-}}\Gamma(x)=\lim_{x\to 0^{-}}\frac{\cancelto{\Gamma(1)=1}{% \Gamma(x+1)}}{x}=-\infty$ (5.140)

e

$\lim_{x\to 0^{+}}\Gamma(x)=\lim_{x\to 0^{+}}\frac{\cancelto{\Gamma(1)=1}{% \Gamma(x+1)}}{x}=\infty$ (5.141)
b)

$\nexists\Gamma(p)$ , com $p$ inteiro negativo

De fato, isto pode ser mostrado por indução a partir do item a) e da propriedade (5.124). Verifique!

Observação 5.2.2.

Para números não naturais $x$ , o valor de $\Gamma(x)$ só pode ser computado via técnicas de cálculo numérico. Uma das exceções, $\Gamma(\frac{1}{2})$ , de fato

	$\displaystyle\Gamma\left(\frac{1}{2}\right)$	$\displaystyle=\int_{0}^{\infty}z^{\frac{1}{2}-1}e^{-z}\,dz$		(5.142)
		$\displaystyle=\int_{0}^{\infty}\frac{e^{-z}}{\sqrt{z}}\,dz$		(5.143)

Fazendo a substituição $u=\sqrt{z}$ , temos $\displaystyle du=\frac{dz}{2\sqrt{z}}=\frac{dz}{2u}$ , obtemos

$\displaystyle\Gamma\left(\frac{1}{2}\right)$	$\displaystyle=\int_{0}^{\infty}\frac{e^{-u^{2}}}{u}\cdot 2u\,du$	(5.144)
	$\displaystyle=2\int_{0}^{\infty}e^{-u^{2}}\,du$	(5.145)
	$\displaystyle=\int_{-\infty}^{\infty}e^{-u^{2}}\,du$	(5.146)

Esta última é a conhecida integral de Gauss, a qual tem valor

\int_{-\infty}^{\infty}e^{-u^{2}}\,du=\sqrt{\pi}.

(5.147)

Logo, concluímos que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\Gamma\left(% \frac{1}{2}\right)=\sqrt{\pi}}.

(5.148)

5.2.2 Função beta

Assista no YouTube

Assista no archive.org!

Escute a audioleitura!

A função beta (ou, integral de Euler de primeiro tipo) é definida por

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}B(x,y)=\int_{0% }^{1}z^{x-1}(1-z)^{y-1}\,dz},

(5.149)

para quaisquer números reais positivos $x$ e $y$ .

Sua relação com a função gama é dada por

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}B(x,y)=\frac{% \Gamma(x)\Gamma(y)}{\Gamma(x+y)}}.

(5.150)

De fato, temos

	$\displaystyle\Gamma(x)\Gamma(y)$	$\displaystyle=\int_{0}^{\infty}u^{x-1}e^{-u}\,du\cdot\int_{0}^{\infty}v^{y-1}e% ^{-v}\,dv$		(5.151)
		$\displaystyle=\int_{v=0}^{\infty}\int_{u=0}^{\infty}u^{x-1}v^{y-1}e^{-(u+v)}\,% du\,dv$		(5.152)

Fazendo a mudança de variáveis $u=zt$ e $v=z(1-t)$ , temos a jacobiana

$\displaystyle J(u,v)$	$\displaystyle=\begin{vmatrix}\frac{\partial u}{\partial z}&\frac{\partial u}{% \partial t}\\ \frac{\partial v}{\partial z}&\frac{\partial v}{\partial t}\end{vmatrix}$	(5.155)
	$\displaystyle=\begin{vmatrix}t&z\\ (1-t)&-z\end{vmatrix}$	(5.158)
	$\displaystyle=-z.$	(5.159)

Logo,

$\displaystyle\Gamma(x)\Gamma(y)$	$\displaystyle=\int_{z=0}^{\infty}\int_{t=0}^{1}(zt)^{x-1}[z(1-t)]^{y-1}e^{-[zt% +z(1-t)]}\,\|J(u,v)\|\,dt\,dz$	(5.160)
	$\displaystyle=\int_{z=0}^{\infty}z^{x+y-1}e^{-z}\,dz\cdot\int_{t=0}^{1}t^{x-1}% (1-t)^{y-1}\,dt$	(5.161)
	$\displaystyle=\Gamma(x+y)B(x,y),$	(5.162)

o que nos fornece (5.150).

Exemplo 5.2.2.

B\left(\frac{1}{2},\frac{1}{2}\right)=\pi.

(5.163)

De fato, de (5.150), temos

$\displaystyle B\left(\frac{1}{2},\frac{1}{2}\right)$	$\displaystyle=\frac{\Gamma\left(\frac{1}{2}\right)\Gamma\left(\frac{1}{2}% \right)}{\Gamma\left(\frac{1}{2}+\frac{1}{2}\right)}$	(5.164)
	$\displaystyle=\frac{\sqrt{\pi}\sqrt{\pi}}{\Gamma(1)}$	(5.165)
	$\displaystyle=\pi.$	(5.166)

Para $n$ e $m$ números naturais não nulos, a propriedade (5.150) mostra que a função beta guarda a seguinte relação com os coeficientes binomiais

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}B(n,m)=\frac{n% +m}{nm}\cdot\frac{1}{\binom{n+m}{n}}},

(5.167)

onde no denominador do último termo temos o coeficiente binomial

\binom{n+m}{n}=\frac{(n+m)!}{n!(n+m-n)!}=\frac{(n+m)!}{n!m!}.

(5.168)

De fato, (5.167) decorre de (5.150), pois

$\displaystyle B(n,m)$	$\displaystyle=\frac{\Gamma(n)\Gamma(m)}{\Gamma(n+m)}$	(5.169)
	$\displaystyle=\frac{(n-1)!(m-1)!}{(n+m-1)!}$	(5.170)
	$\displaystyle=\frac{n!m!}{(n+m)!}\frac{n+m}{nm}$	(5.171)
	$\displaystyle=\frac{n+m}{nm}\cdot\frac{1}{\frac{(n+m)!}{n!m!}}$	(5.172)
	$\displaystyle=\frac{n+m}{nm}\cdot\frac{1}{\binom{n+m}{n}}.$	(5.173)

Exercícios resolvidos

ER 5.2.1.

Calcule $\displaystyle\Gamma\left(\frac{3}{2}\right)$ .

Solução.

Da propriedade (5.124) e de (5.148) , temos

$\displaystyle\Gamma\left(\frac{3}{2}\right)$	$\displaystyle=\Gamma\left(\frac{1}{2}+1\right)$	(5.174)
	$\displaystyle=\frac{1}{2}\Gamma\left(\frac{1}{2}\right)$	(5.175)
	$\displaystyle=\frac{1}{2}\sqrt{\pi}.$	(5.176)

ER 5.2.2.

Verifique que

n!=\int_{0}^{1}(-\ln s)^{n}\,ds.

(5.177)

Solução.

Fazemos as mudanças de variáveis $t=-\ln s$ , donde

	$\displaystyle dt=-\frac{1}{s}\,ds$		(5.178)
	$\displaystyle\Rightarrow ds=-e^{-t}\,dt$		(5.179)

Logo, temos

$\displaystyle\int_{0}^{1}(-\ln s)^{n}\,ds$	$\displaystyle=-\int_{\infty}^{0}t^{n}e^{-t}\,dt$	(5.180)
	$\displaystyle=\int_{0}^{\infty}t^{n}e^{-t}\,dt$	(5.181)
	$\displaystyle=\Gamma(n+1)$	(5.182)
	$\displaystyle=n!$	(5.183)

ER 5.2.3.

Calcule $B(2,3)$ .

Solução.

Da propriedade (5.150), temos

$\displaystyle B(2,3)$	$\displaystyle=\frac{\Gamma(2)\Gamma(3)}{\Gamma(2+3)}$	(5.184)
	$\displaystyle=\frac{1!\cdot 2!}{4!}$	(5.185)
	$\displaystyle=\frac{2}{24}$	(5.186)
	$\displaystyle=\frac{1}{12}.$	(5.187)

Exercícios

E. 5.2.1.

Calcule

a)

$\Gamma(1)$
b)

$\Gamma(3)$
c)

$\Gamma(5)$
d)

$\Gamma(7)$

Resposta.

a) 1; b) 2; c) 24; d) 720

E. 5.2.2.

Calcule

a)

$\Gamma\left(\frac{3}{2}\right)$
b)

$\Gamma\left(\frac{5}{2}\right)$
c)

$\Gamma\left(\frac{7}{2}\right)$

Resposta.

a) $\frac{\sqrt{\pi}}{2}$ ; b) $\frac{3\sqrt{\pi}}{4}$ ; c) $\frac{15\sqrt{\pi}}{8}$

E. 5.2.3.

Calcule

a)

$\Gamma\left(-\frac{1}{2}\right)$
b)

$\Gamma\left(-\frac{3}{2}\right)$

Resposta.

a) $-2\sqrt{\pi}$ ; b) $\frac{4\sqrt{\pi}}{3}$

E. 5.2.4.

Calcule

a)

$B(1,1)$
b)

$B(2,2)$
c)

$B(3,2)$

Resposta.

a) 1; b) $\frac{1}{6}$ ; c) $\frac{1}{12}$ ;

E. 5.2.5.

Calcule

a)

$B\left(\frac{1}{2},\frac{1}{2}\right)$
b)

$B\left(1,\frac{1}{2}\right)$
c)

$B\left(\frac{1}{2},\frac{3}{2}\right)$

Resposta.

a) $\pi$ ; b) 2; c) $\frac{\pi}{2}$

E. 5.2.6.

Verifique que

B(1,x)=\frac{1}{x},

(5.188)

para todo $x$ número real positivo.

Resposta.

Dica: use (5.150).

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |