Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

1 Limites 1.5 Limites infinitos 1.7 Limites e desigualdades

1.6 Continuidade

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.6.1 Definição de função contínua

Dizemos que uma função $f$ é contínua em um ponto $x_{0}$ , quando $f(x_{0})$ está definida, existe o limite

\lim_{x\to x_{0}}f(x)

(1.274)

\lim_{x\to x_{0}}f(x)=f(x_{0}).

(1.275)

Usando de limites laterais, definimos os conceitos de função contínua à esquerda ou à direta. Quando a função $f$ não é contínua em um dado ponto $x_{0}$ , dizemos que $f$ é descontínua neste ponto.

Exemplo 1.6.1.

Consideremos a seguinte função

f(x)=\left\{\begin{array}[]{ll}\frac{x-2}{(x+1)(x-2)}&,x\neq 2,\\ -4&,x=2.\end{array}\right.

(1.276)

Na Figura 1.23, temos um esboço do gráfico de $f$ .

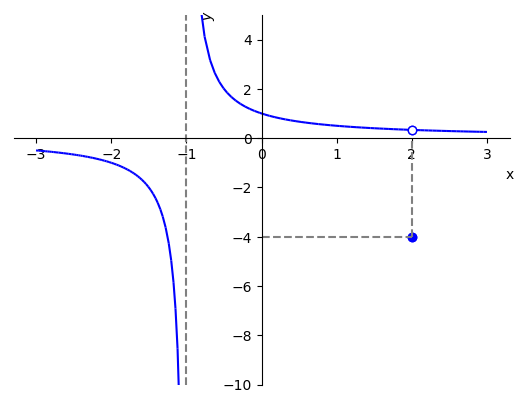
Refer to caption — Figura 1.23: Esboço do gráfico da função $f$ definida no Exemplo 1.6.1.

Vejamos a continuidade desta função nos seguintes pontos:

a)

$x=-2$ . Neste ponto, temos $f(-2)=-1$ e

$\displaystyle\lim_{x\to-2}\frac{x-2}{(x+1)(x-2)}$ (1.277)

$\displaystyle=\frac{-4}{-1\cdot(-4)}=-1=f(-2).$ (1.278)

Com isso, concluímos que $f$ é contínua no ponto $x=-2$ .
b)

$x=-1$ . Neste ponto,

$\displaystyle f(-1)=\frac{(x-2)}{(x+1)(x-2)}$ (1.279)

$\displaystyle=\frac{1}{x-1}=\frac{1}{0}$ (1.280)

logo, f(-1) não está definido e, portanto, $f$ é descontínua neste ponto. Observemos que $f$ tem uma assíntota vertical em $x=-1$ , verifique!
c)

$x=2$ . Neste ponto, temos $f(2)=-4$ e

$\displaystyle\lim_{x\to 2}\frac{x-2}{(x+1)(x-2)}$ (1.281)

$\displaystyle=\lim_{x\to 2}\frac{1}{x+1}=\frac{1}{3}\neq f(2).$ (1.282)

Portanto, concluímos que $f$ é descontínua em $x=2$ .

Uma função $f$ é dita ser contínua em um intervalo $(a,b)$ , quando $f$ é contínua em todos os pontos $x_{0}\in(a,b)$ . Para intervalos, $[a,b)$ , $(a,b]$ ou $[a,b]$ , empregamos a noção de continuidade lateral nos pontos de extremos fechados dos intervalos. Quando uma função é contínua em $(-\infty,\infty)$ , dizemos que ela é contínua em toda parte.

Exemplo 1.6.2.

(Continuidade da função valor absoluto.) A função valor absoluto é contínua em toda parte. De fato, ela é definida por

|x|=\left\{\begin{array}[]{ll}x&,x\geq 0,\\ -x&,x<0.\end{array}\right.

(1.283)

Veja o esboço do gráfico desta função na Figura 1.24.

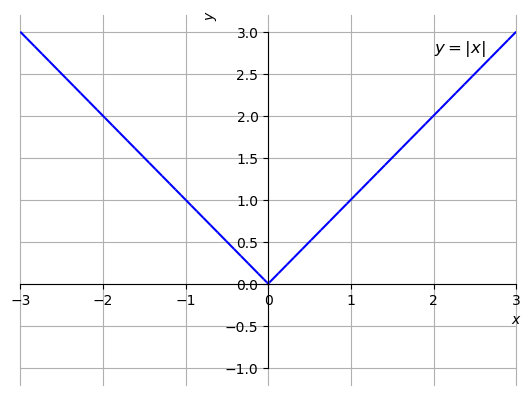
Observamos que para $x\in(-\infty,0)$ temos $|x|=x$ que é contínua para todos estes valores de $x$ . Também, para $x\in(0,\infty)$ temos $|x|=-x$ que é contínua para todos estes valores de $x$ . Agora, em $x=0$ , temos $|0|=0$ e

	$\displaystyle\lim_{x\to 0^{+}}\|x\|$	$\displaystyle=\lim_{x\to 0^{+}}x=0,$		(1.284)
	$\displaystyle\lim_{x\to 0^{-}}\|x\|$	$\displaystyle=\lim_{x\to 0^{-}}-x=0.$		(1.285)

Logo,

\lim_{x\to 0}|x|=0=|0|.

(1.286)

Com tudo isso, concluímos que a função valor absoluto é contínua em toda parte.

1.6.2 Propriedades de funções contínuas

Se $f$ e $g$ são funções contínuas em $x=c_{0}$ e $k$ um número real, então também são contínuas em $x=x_{0}$ as funções:

a)

$k\cdot f$
b)

$f\pm g$
c)

$f\cdot g$
d)

$f/g$ , se $g(x_{0})\neq 0$
e)

$f^{k}$ , se existe $f^{k}(x_{0})$ .

Exemplo 1.6.3.

Temos que $f(x)=x$ e $g(x)=|x|$ são exemplos de funções contínuas em toda parte. Segue das propriedades acima que:

a)

$f_{a}(x)=2x$ é contínua em toda parte.
b)

$f_{b}(x)=x+|x|$ é contínua em toda parte.
c)

$f_{c}(x)=2x|x|$ é contínua em toda parte.
d)

$f_{d}(x)=\frac{|x|}{x}$ é contínua para todo $x\in\mathbb{R}\setminus\{0\}$ .
e)

$f_{e}(x)=x^{2}$ é contínua em toda parte.

Exemplo 1.6.4.

Polinômios são contínuos em toda parte. Isto é, se $p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_{1}x+a_{0}$ , então

\lim_{x\to x_{0}}p(x)=p(x_{0}),

(1.287)

para qualquer $x_{0}\in\mathbb{R}$ . Por exemplo,

\lim_{x\to-1}2-x^{2}+x^{5}=2-(-1)^{2}+(-1)^{5}=0.

(1.288)

Exemplo 1.6.5.

Funções racionais $r(x)=p(x)/q(x)$ são contínuas em todos os pontos de seus domínios. Por exemplo, a função racional

f(x)=\frac{x-1}{x^{2}-1},

(1.289)

é descontínua nos pontos

x^{2}-1=0\Rightarrow x=\pm 1,

(1.290)

pois $f$ não está definida nestes pontos. Agora, para $x_{0}\neq 1$ e $x_{0}\neq-1$ , temos

	$\displaystyle\lim_{x\to x_{0}}f(x)$		(1.291)
	$\displaystyle=\lim_{x\to x_{0}}\frac{x-1}{x^{2}-1}$		(1.292)
	$\displaystyle=\frac{x_{0}-1}{x_{0}^{2}-1}=f(x_{0}).$		(1.293)

Por exemplo,

\lim_{x\to 0}f(x)=\frac{0-1}{0^{2}-1}=1=f(0).

(1.294)

Ou seja, $f$ é contínua nos intervalos $(-\infty,-1)\cup(-1,1)\cup(1,\infty)$ , que coincide com seu domínio.

Observação 1.6.1.

São contínuas em todo seu domínio as funções potência, polinomiais, racionais, trigonométricas, exponenciais e logarítmicas.

Se $f$ é contínua no ponto $x_{0}$ e $g$ é contínua no ponto $f(x_{0})$ , então $g\circ f$ é contínua no ponto $x_{0}$ .

Exemplo 1.6.6.

Vejamos os seguintes casos:

a)

$y=\sqrt{x^{2}-1}$ é descontínua nos pontos $x$ tais que

$x^{2}-1<0\Rightarrow-1<x<1.$ (1.295)

Isto é, esta função é contínua em $(-\infty,-1]\cup[1,\infty)$ .
b)

$\displaystyle y=\left|\frac{x-1}{x^{2}-1}\right|$ é descontínua nos pontos $x$ tais que

$x^{2}-1=0\Rightarrow x=\pm 1.$ (1.296)

Exemplo 1.6.7.

Podemos explorar a continuidade para calcularmos limites. Por exemplo,

\lim_{x\to 0}\sqrt{x+4}\cdot e^{\operatorname{sen}x}=\sqrt{\lim_{x\to 0}x+4}% \cdot e^{\operatorname{sen}\lim_{x\to 0}x}=\sqrt{4}\cdot e^{0}=2.

(1.297)

Teorema do Valor Intermediário

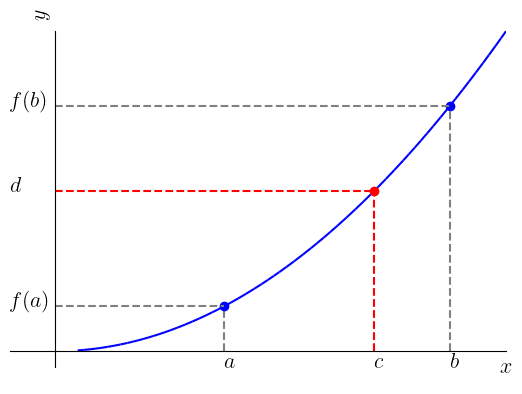
O Teorema do Valor Intermediário estabelece que qualquer dada função $f$ contínua em um intervalo $[a,b]$ , assume todos os valores entre $f(a)$ e $f(b)$ . Consulte a Figura 1.25.

Teorema 1.6.1.

(Teorema do valor intermediário) Seja $f$ função contínua em um intervalo fechado $[a,b]$ . Se $d$ é um número entre $f(a)$ e $f(b)$ , então existe $c\in[a,b]$ tal que $f(c)=d$ .

Exemplo 1.6.8.

Podemos afirmar que $f(x)=x^{3}-x-1$ tem (pelo menos) um zero no intervalo $(0,2)$ . De fato, $f$ é contínua no intervalo $[0,2]$ e, pelo teorema do valor intermediário, assume todos os valores entre $f(0)=-1<0$ e $f(2)=5>0$ . Observemos que $y=0$ está entre $f(0)$ e $f(2)$ . Veja a Figura 1.26.

1.6.3 Exercícios resolvidos

ER 1.6.1.

Encontre os pontos de continuidade da função

f(x)=\frac{|x|}{x}.

(1.298)

Solução.

Observamos que a função é descontínua em $x=0$ , pois não está definida neste ponto. Agora, para $x<0$ , temos

f(x)=\frac{|x|}{x}=\frac{-x}{x}=-1.

(1.299)

Ou seja, para $x<0$ a função é constante igual a $-1$ e, portanto, contínua.

Para $x>0$ , temos

f(x)=\frac{|x|}{x}=\frac{x}{x}=1.

(1.300)

I.e., para $x>0$ a função é constante igual a $1$ e, portanto, contínua.

Concluímos que $f(x)$ é contínua em $\mathbb{R}\setminus\{0\}$ . Faça o esboço do gráfico desta função!

ER 1.6.2.

Encontre os pontos de continuidade da função

f(x)=\ln\left(\frac{x+1}{x-1}\right).

(1.301)

Solução.

A função $f$ pode ser vista como a composição da função logaritmo natural $g(x)=\ln x$ com a função racional $\displaystyle h(x)=\frac{x+1}{x-1}$ . Observamos que:

a)

a função logaritmo natural é contínua em todo o seu domínio, i.e. $g$ é contínua para todo $x>0$ ;
b)

a função racional $\displaystyle h(x)=\frac{x+1}{x-1}$ é contínua para todo $x\neq 1$ .

Lembrando que a composição de funções contínuas é contínua, temos que a função $f(x)=g(h(x))$ é contínua nos pontos de continuidade da função $h$ tais que $h(x)>0$ , i.e. para $x\neq 1$ e

\displaystyle\frac{x+1}{x-1}>0.

(1.302)

Fazendo o estudo de sinal

vemos que $h(x)>0$ em $(-\infty,-1)\cup(1,\infty)$ .

Em resumo, $h$ é contínua em $(0,\infty)$ e $g$ é contínua e positiva em $(-\infty,-1)\cup(1,\infty)$ . A função $f=(h\circ g)$ é contínua na interseção destes conjuntos, i.e. $f$ é contínua em $(1,\infty)$ .

1.6.4 Exercícios

E. 1.6.1.

Encontre os pontos de continuidade da função

f(x)=\frac{x^{3}-27}{x^{2}-3x+2}.

(1.303)

Resposta.

$\mathbb{R}\setminus\{1,2\}$ .

E. 1.6.2.

Encontre os pontos de continuidade da função

f(x)=\sqrt{\frac{x^{3}-27}{x^{2}-3x+2}}.

(1.304)

Resposta.

$(1,2)\cup(3,\infty)$ .

E. 1.6.3.

Calcule

a)

$\displaystyle\lim_{x\to-1}e^{x^{2}-1}$
b)

$\displaystyle\lim_{x\to\sqrt{2}}\ln|x^{2}-1|$

Resposta.

a) $1$ ; b) $0$

E. 1.6.4.

Calcule

\lim_{x\to\pi}\ln\left(\frac{\operatorname{sen}\frac{x}{2}-\cos x}{2}\right).

(1.305)

Resposta.

$0$

E. 1.6.5.

Calcule o valor de $c$ de forma que a seguinte função seja contínua em $x=1$ .

f(x)=\left\{\begin{array}[]{ll}\frac{x-1}{x^{2}-1}&,x\neq 1\\ c&,x=1\end{array}\right.

(1.306)

Resposta.

$c=\frac{1}{2}$

E. 1.6.6.

(Aplicação.) O fenômeno de desintegração espontânea do núcleo de um átomo com a emissão de algumas radiações é chamado de radioatividade¹¹¹¹endnote: ¹¹Fonte: Wikipédia.. A lei fundamental do decaimento radiativo estabelece que a taxa de decaimento é proporcional ao número de átomos que ainda não decaíram. Isto nos fornece a equação da lei básica da radioatividade

N=N_{0}e^{-\lambda t}

(1.307)

onde, $N=N(t)$ é o número de átomos no tempo $t$ , $N_{0}\geq 0$ é o número de átomos presentes no tempo inicial $t=0$ e $\lambda>0$ é a constante de decaimento. Qual a tendência de $N=N(t)$ quando a taxa de decaimento $\lambda\to 0^{+}$ .

Resposta.

$N(t)\to N_{0}$ quando $\lambda\to 0^{+}$

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |

	$\displaystyle\lim_{x\to-2}\frac{x-2}{(x+1)(x-2)}$		(1.277)
	$\displaystyle=\frac{-4}{-1\cdot(-4)}=-1=f(-2).$		(1.278)

	$\displaystyle f(-1)=\frac{(x-2)}{(x+1)(x-2)}$		(1.279)
	$\displaystyle=\frac{1}{x-1}=\frac{1}{0}$		(1.280)

	$\displaystyle\lim_{x\to 2}\frac{x-2}{(x+1)(x-2)}$		(1.281)
	$\displaystyle=\lim_{x\to 2}\frac{1}{x+1}=\frac{1}{3}\neq f(2).$		(1.282)