Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

1 Limites 1.6 Continuidade 1.8 Exercícios finais

1.7 Limites e desigualdades

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Se $f$ e $g$ são funções tais que $f(x){\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}<}g(x)$ para todo $x$ em um certo intervalo aberto contendo $x_{0}$ , exceto possivelmente em $x=x_{0}$ , e existem os limites de $f$ e $g$ no ponto $x=x_{0}$ , então

\lim_{x\to x_{0}}f(x){\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{% rgb}{0,0,1}\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}% \leq}\lim_{x\to x_{0}}g(x).

(1.308)

Observe que a tomada do limite não preserva a desigualdade estrita.

Exemplo 1.7.1.

As funções $f(x)=x^{2}/3$ e $g(x)=x^{2}/2$ são tais que $f(x)<g(x)$ para todo $x\neq 0$ . Ainda, temos

\lim_{x\to 0}f(x)=0\quad\text{e}\quad\lim_{x\to 0}g(x)=0.

(1.309)

Observação 1.7.1.

A preservação da desigualdade também ocorre para limites laterais. Mais precisamente, se $f$ e $g$ são funções tais que $f(x)<g(x)$ para todo $x<x_{0}$ e existem os limites laterais à esquerda de $f$ e $g$ no ponto $x=x_{0}$ , então

\lim_{x\to x_{0}^{-}}f(x)\leq\lim_{x\to x_{0}^{-}}g(x).

(1.310)

Vale o resultado análogo para limite lateral à direita e limites no infinito.

1.7.1 Limites de funções limitadas

Se $f(x)\leq L$ para todo $x$ em um intervalo aberto contendo $x_{0}$ , exceto possivelmente em $x_{0}$ , então

\lim_{x\to x_{0}}f(x)\leq L.

(1.311)

Resultados análogos valem para limites laterais e limites no infinito.

Exemplo 1.7.2.

Vamos calcular o seguinte limite

\lim_{x\to\infty}e^{-x}\operatorname{sen}x.

(1.312)

Como $|\operatorname{sen}x|\leq 1$ , temos

	$\displaystyle\lim_{x\to\infty}e^{-x}\operatorname{sen}x\leq\lim_{x\to\infty}e^% {-x}=0,$		(1.313)
	$\displaystyle\lim_{x\to\infty}e^{-x}\operatorname{sen}x\geq\lim_{x\to\infty}-e% ^{-x}=0.$		(1.314)

Logo, temos

\lim_{x\to\infty}e^{-x}\operatorname{sen}x=0.

(1.315)

1.7.2 Teorema do confronto

Teorema 1.7.1.

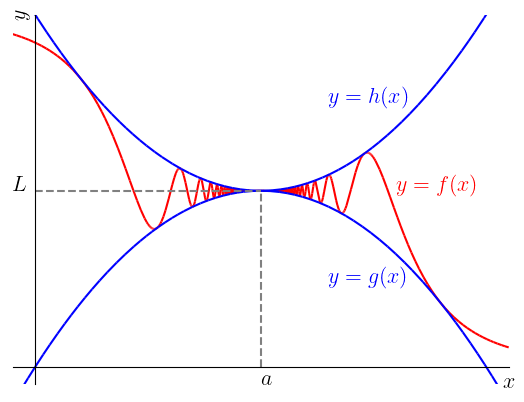
(Teorema do confronto) Se $g(x)\leq f(x)\leq h(x)$ para todo $x$ em um intervalo aberto contendo $a$ , exceto possivelmente em $x=a$ (consulte a Figura 1.27), e

\lim_{x\to a}g(x)=\lim_{x\to a}h(x)=L,

(1.316)

então

\lim_{x\to a}f(x)=L.

(1.317)

Refer to caption — Figura 1.27: Ilustração sobre o Teorema 1.7.1.

Demonstração.

Da preservação da desigualdade, temos

\lim_{x\to a}g(x)\leq\lim_{x\to a}f(x)\leq\lim_{x\to a}h(x)

(1.318)

donde

L\leq\lim_{x\to a}f(x)\leq L.

(1.319)

∎

Exemplo 1.7.3.

Toda função $f(x)$ tal que $-1+x^{2}/2\leq f(x)\leq-1+x^{2}/3$ , para todo $x\neq 0$ , tem

\lim_{x\to 0}f(x)=-1.

(1.320)

Observação 1.7.2.

O Teorema do confronto também se aplica a limites laterais.

Exemplo 1.7.4.

\lim_{x\to 0}\operatorname{sen}x=0.

(1.321)

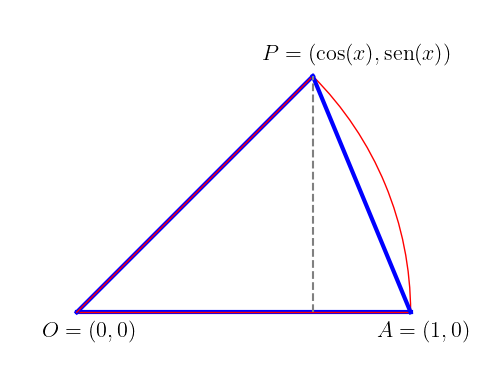
De fato, começamos assumindo $0<x<\pi/2$ . Tomando $O=(0,0)$ , $A=(1,0)$ e $P=(\cos x,\operatorname{sen}x)$ (consulte a Figura 1.28), observamos que

\text{\'{A}rea do tri\^{a}ng.}OAP<\text{\'{A}rea do setor}OAP,

(1.322)

i.e.

\frac{\operatorname{sen}x}{2}<\frac{x}{2}\Rightarrow\operatorname{sen}x<x,

(1.323)

para todo $0<x<\pi/2$ .

É certo que $\operatorname{sen}x<-x$ para $-\pi/2<x<0$ . Com isso e o resultado acima, temos

\operatorname{sen}x\leq|x|,\quad-\pi/2<x<\pi/2.

(1.324)

Lembrando que $\operatorname{sen}x$ é uma função ímpar, temos

-|x|\leq-\operatorname{sen}x=\operatorname{sen}-x,\quad-\pi/2<x<\pi/2.

(1.325)

Logo, de (1.324) e (1.325), temos

-|x|\leq\operatorname{sen}x\leq|x|.

(1.326)

Por fim, como

\lim_{x\to 0}-|x|=\lim_{x\to 0}|x|=0,

(1.327)

do Teorema do confronto, concluímos

\lim_{x\to 0}\operatorname{sen}x=0.

(1.328)

Observação 1.7.3.

Do exemplo anterior (Exemplo 1.7.4), podemos mostrar que

\lim_{x\to 0}\cos x=1.

(1.329)

De fato, da identidade trigonométrica de ângulo metade

\operatorname{sen}^{2}\frac{x}{2}=\frac{1-\cos x}{2}

(1.330)

temos

\cos x=1+2\operatorname{sen}^{2}\frac{x}{2}.

(1.331)

Então, aplicando as regras de cálculo de limites, obtemos

	$\displaystyle\lim_{x\to 0}\cos x$	$\displaystyle=\lim_{x\to 0}\left[1+2\operatorname{sen}^{2}\frac{x}{2}\right]$		(1.332)
		$\displaystyle=1+2\left(\lim_{x\to 0}\operatorname{sen}\frac{x}{2}\right)^{2}.$		(1.333)

Agora, fazemos a mudança de variável $y=x/2$ . Neste caso, temos $y\to 0$ quando $x\to 0$ e, então

\lim_{x\to 0}\operatorname{sen}\frac{x}{2}=\lim_{y\to 0}\operatorname{sen}y=0.

(1.334)

Então, retornando a equação (1.333), concluímos

\lim_{x\to 0}\cos x=1.

(1.335)

1.7.3 Limites envolvendo $(\operatorname{sen}x)/x$

Verificamos o seguinte resultado

\lim_{x\to 0}\frac{\operatorname{sen}x}{x}=1.

(1.336)

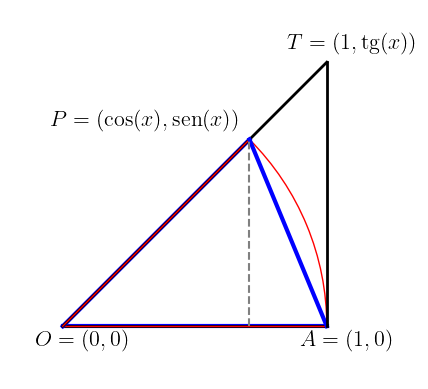
Para verificarmos este resultado, calcularemos os limites laterais à esquerda e à direita. Começamos com o limite lateral a direita e assumimos $0<x<\pi/2$ . Sendo os pontos $O=(0,0)$ , $P=(\cos x,\operatorname{sen}x)$ , $A=(1,0)$ e $T=(1,\operatorname{tg}x)$ (consulte Figura 1.29), observamos que

\text{\'{A}rea do tri\^{a}ng. }OAP<\text{\'{A}rea do setor}OAP<\text{\'{A}rea % do tri\^{a}ng. }OAT.

(1.337)

Ou seja, temos

\frac{\operatorname{sen}x}{2}<\frac{x}{2}<\frac{\operatorname{tg}x}{2}.

(1.338)

Multiplicando por $2$ e dividindo por $\operatorname{sen}x$ ¹²¹²endnote: ¹² $\operatorname{sen}x>0$ para todo $0<x<\pi/2$ ., obtemos

1<\frac{x}{\operatorname{sen}x}<\frac{1}{\cos x}.

(1.339)

Tomando os recíprocos, temos

1>\frac{\operatorname{sen}x}{x}>\cos x.

(1.340)

Agora, passando ao limite

1=\lim_{x\to 0^{+}}1\geq\lim_{x\to 0^{+}}\frac{\operatorname{sen}x}{x}\geq\lim% _{x\to 0^{+}}\cos x=1.

(1.341)

Logo, concluímos que

\lim_{x\to 0^{+}}\frac{\operatorname{sen}x}{x}=1.

(1.342)

Agora, usando o fato de que $\operatorname{sen}x/x$ é uma função par, temos

	$\displaystyle\lim_{x\to 0^{-}}\frac{\operatorname{sen}x}{x}$	$\displaystyle=\lim_{x\to 0^{-}}\frac{\operatorname{sen}(-x)}{-x}$		(1.343)
		$\displaystyle=\lim_{x\to 0^{+}}\frac{\operatorname{sen}x}{x}=1.$		(1.344)

Calculados os limites laterais, concluímos o que queríamos.

Exemplo 1.7.5.

Com o resultado acima e as regras de cálculo de limites, temos

\lim_{x\to 0}\frac{\cos(x)-1}{x}=0.

(1.345)

Veja o Exercício 1.7.4.

1.7.4 Exercícios resolvidos

ER 1.7.1.

Sabendo que $x^{3}\leq f(x)\leq\sqrt{x}$ para $0<x<1$ , calcule

\lim_{x\to 0^{+}}f(x).

(1.346)

Solução.

Pelo Teorema do Confronto, temos

\lim_{x\to 0^{+}}\cancelto{0}{x^{3}}\leq\lim_{x\to 0^{+}}f(x)\leq\lim_{x\to 0^% {+}}\cancelto{0}{\sqrt{x}}.

(1.347)

Logo,

\lim_{x\to 0^{+}}f(x)=0.

(1.348)

1.7.5 Exercícios

| | | |

1.7 Limites e desigualdades

Exemplo 1.7.1.

Observação 1.7.1.

1.7.1 Limites de funções limitadas

Exemplo 1.7.2.

1.7.2 Teorema do confronto

Teorema 1.7.1.

Demonstração.

Exemplo 1.7.3.

Observação 1.7.2.

Exemplo 1.7.4.

Observação 1.7.3.

1.7.3 Limites envolvendo (sen⁡x)/x

Exemplo 1.7.5.

1.7.4 Exercícios resolvidos

ER 1.7.1.

Solução.

1.7.5 Exercícios

E. 1.7.1.

Resposta.

E. 1.7.2.

Resposta.

E. 1.7.3.

Resposta.

E. 1.7.4.

Resposta.

E. 1.7.5.

Resposta.

Envie seu comentário

1.7.3 Limites envolvendo $(\operatorname{sen}x)/x$