Cálculo I

3 Derivadas 3.5 Regras básicas de derivação 3.7 Linearização e diferenciais

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.6 Derivadas de funções trigonométricas

Começamos pela derivada da função seno. Pela definição da derivada, temos

	$\displaystyle\operatorname{sen}^{\prime}x=\lim_{h\to 0}\frac{\operatorname{sen% }(x+h)-\operatorname{sen}x}{h}$		(3.327)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\operatorname{sen}(x)\cos(h)+\cos% (x)\operatorname{sen}(h)-\operatorname{sen}x}{h}$		(3.328)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\operatorname{sen}(x)\frac{\cos(h)-1}{h% }+\cos(x)\frac{\operatorname{sen}h}{h}$		(3.329)
	$\displaystyle\text{}\quad=\operatorname{sen}(x)\lim_{h\to 0}\frac{\cos(h)-1}{h% }+\cos(x)\lim_{h\to 0}\frac{\operatorname{sen}h}{h}.$		(3.330)

Usando do teorema do confronto para limites de funções, podemos mostrar que⁶⁶6Consultemos aSeção 2.7.4.

\lim_{h\to 0}\frac{\operatorname{sen}h}{h}=1\quad\text{e}\quad\lim_{h\to 0}% \frac{\cos(h)-1}{h}=0.

(3.331)

Logo, temos

\boldsymbol{\operatorname{sen}^{\prime}x=\cos x}.

(3.332)

De forma similar, temos

	$\displaystyle\cos^{\prime}x=\lim_{h\to 0}\frac{\cos(x+h)-\cos x}{h}$		(3.333)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\frac{\cos(x)\cos(h)-\operatorname{sen}% (x)\operatorname{sen}(h)-\cos x}{h}$		(3.334)
	$\displaystyle\text{}\quad=\lim_{h\to 0}\cos(x)\frac{\cos(h)-1}{h}-% \operatorname{sen}(x)\frac{\operatorname{sen}h}{h}$		(3.335)
	$\displaystyle\text{}\quad=\cos(x)\lim_{h\to 0}\cancelto{0}{\frac{\cos(h)-1}{h}% }-\operatorname{sen}(x)\lim_{h\to 0}\cancelto{0}{\frac{\operatorname{sen}h}{h}}.$		(3.336)

Ou seja,

\boldsymbol{\cos^{\prime}x=-\operatorname{sen}x}.

(3.337)

Exemplo 3.6.1.

A derivada de $f(x)=\operatorname{sen}^{2}x+\cos^{2}x$ é

	$\displaystyle f^{\prime}(x)=(\operatorname{sen}^{2}x+\cos^{2}x)^{\prime}$		(3.338)
	$\displaystyle\text{}\quad=(\operatorname{sen}^{2}x)^{\prime}+(\cos^{2}x)^{\prime}$		(3.339)
	$\displaystyle\text{}\quad=(\operatorname{sen}x\cdot\operatorname{sen}x)^{% \prime}+(\cos x\cdot\cos x)^{\prime}$		(3.340)
	$\displaystyle\text{}\quad=\cos x\cdot\operatorname{sen}x+\operatorname{sen}x% \cdot\cos x-\operatorname{sen}x\cdot\cos x-\cos x\cdot\operatorname{sen}x$		(3.341)
	$\displaystyle\text{}\quad=0,$		(3.342)

conforme esperado⁷⁷7Lembremos da identidade trigonométrica fundamental $\operatorname{sen}^{2}(x)+\cos^{2}(x)\equiv 1$ ..

Código 59: Python

⬇

1from sympy import diff, sin, cos

2from sympy.abc import x

3diff(sin(x)**2 + cos(x)**2, x)

Conhecidas as derivadas da função seno e cosseno, podemos obter as derivadas das demais funções trigonométricas pela regra do quociente. Temos:

•

$\boldsymbol{\operatorname{tg}^{\prime}x=\sec^{2}x}$

	$\displaystyle\operatorname{tg}^{\prime}x=\left(\frac{\operatorname{sen}x}{\cos x% }\right)^{\prime}$		(3.343)
	$\displaystyle\text{}\quad=\frac{\operatorname{sen}^{\prime}x\cos x-% \operatorname{sen}x\cos^{\prime}x}{\cos^{2}x}$		(3.344)
	$\displaystyle\text{}\quad=\frac{\cos x\cos x+\operatorname{sen}x\operatorname{% sen}x}{\cos^{2}x}$		(3.345)
	$\displaystyle\text{}\quad=\frac{1}{\cos^{2}x}=\left(\frac{1}{\cos x}\right)^{2}$		(3.346)
	$\displaystyle\text{}\quad=\sec^{2}x.$		(3.347)

Código 60: Python

⬇

1from sympy import diff, tan

2from sympy.abc import x

3diff(tan(x), x)

tan(x)**2 + 1

•

$\boldsymbol{\operatorname{cotg}^{\prime}x=-\operatorname{cossec}^{2}x}$

Consultemos a demonstração deste resultado no E.3.6.4.

Código 61: Python

⬇

1from sympy import diff, cot

2from sympy.abc import x

3diff(cot(x), x)

⬇

-cot(x)**2 - 1
•

$\boldsymbol{\sec^{\prime}x=\sec x\operatorname{tg}x}$

$\displaystyle\sec^{\prime}x=\left(\frac{1}{\cos x}\right)^{\prime}$ (3.348)

$\displaystyle\text{}\quad=\frac{-\cos^{\prime}x}{\cos^{2}x}$ (3.349)

$\displaystyle\text{}\quad=\frac{\operatorname{sen}x}{\cos^{2}x}$ (3.350)

$\displaystyle\text{}\quad=\frac{\operatorname{sen}x}{\cos x}\cdot\frac{1}{\cos x}$ (3.351)

$\displaystyle\text{}\quad=\operatorname{tg}x\sec x.$ (3.352)

Código 62: Python

⬇

1from sympy import diff, sec

2from sympy.abc import x

3diff(sec(x), x)

⬇

sec(x)*tan(x)
•

$\boldsymbol{\operatorname{cossec}^{\prime}x=-\operatorname{cossec}x% \operatorname{cotg}x}$

Consultemos a demonstração deste resultado no E.3.6.5.

Código 63: Python

⬇

1from sympy import diff, csc

2from sympy.abc import x

3diff(csc(x), x)

⬇

-cot(x)*csc(x)

Observação 3.6.1.

Os cálculos acima, mostram que as funções trigonométricas são deriváveis em todos os pontos de seus domínios.

Exemplo 3.6.2.

A derivada em relação a $x$ de

f(x)=\frac{x+\operatorname{tg}x}{\sec x}

(3.353)

pode ser calculada como segue

	$\displaystyle f^{\prime}(x)=\left(\frac{x+\operatorname{tg}x}{\sec x}\right)^{\prime}$		(3.354)
	$\displaystyle\text{}\quad=\frac{(x+\operatorname{tg}x)^{\prime}\sec x-(x+% \operatorname{tg}x)\sec^{\prime}x}{\sec^{2}x}$		(3.355)
	$\displaystyle\text{}\quad=\frac{(1+\sec^{2}x)\sec x-(x+\operatorname{tg}x)\sec x% \operatorname{tg}x}{\sec^{2}x}$		(3.356)
	$\displaystyle\text{}\quad=\frac{1+\sec^{2}x-(x+\operatorname{tg}x)% \operatorname{tg}x}{\sec x}.$		(3.357)

3.6.1 Lista de derivadas

	$\displaystyle(ku)^{\prime}=ku^{\prime}$		(3.358)
	$\displaystyle(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}$		(3.359)
	$\displaystyle(uv)^{\prime}=u^{\prime}v+uv^{\prime}$		(3.360)
	$\displaystyle\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{% v^{2}}$		(3.361)
	$\displaystyle(k)^{\prime}=0$		(3.362)
	$\displaystyle(x)^{\prime}=1$		(3.363)
	$\displaystyle(x^{n})^{\prime}=nx^{n-1}$		(3.364)
	$\displaystyle(a^{x})^{\prime}=a^{x}\ln a$		(3.365)
	$\displaystyle(e^{x})^{\prime}=e^{x}$		(3.366)
	$\displaystyle(\log_{a}x)^{\prime}=\frac{1}{x\ln a}$		(3.367)
	$\displaystyle(\ln x)^{\prime}=\frac{1}{x}$		(3.368)
	$\displaystyle\operatorname{sen}^{\prime}x=\cos x$		(3.369)
	$\displaystyle\cos^{\prime}x=-\operatorname{sen}x$		(3.370)
	$\displaystyle\operatorname{tg}^{\prime}x=\sec^{2}x$		(3.371)
	$\displaystyle\operatorname{cotg}^{\prime}x=-\operatorname{cossec}^{2}x$		(3.372)
	$\displaystyle\sec^{\prime}x=\sec x\operatorname{tg}x$		(3.373)
	$\displaystyle\operatorname{cossec}^{\prime}x=-\operatorname{cossec}x% \operatorname{cotg}x$		(3.374)

3.6.2 Exercícios resolvidos

ER 3.6.1.

Encontre a equação da reta tangente ao gráfico da função $y=\operatorname{sen}x$ no ponto $x=0$ . Então, faça os esboços desta função e da reta tangente, em uma mesma figura.

Resolução.

A equação da reta tangente ao gráfico de uma função $y=f(x)$ no ponto $x=x+0$ é

y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0}).

(3.375)

No caso deste exercício, temos $f(x)=\operatorname{sen}x$ e $x_{0}=0$ . Assim sendo, calculamos a derivada em relação a $x$ de $f(x)$ , i.e.

f^{\prime}(x)=\operatorname{sen}^{\prime}x=\cos x.

(3.376)

Segue que a equação da reta tangente é

	$\displaystyle y=f^{\prime}(0)(x-0)+f(0)$		(3.377)
	$\displaystyle y=\cos(0)(x-0)+\operatorname{sen}(0)$		(3.378)
	$\displaystyle y=x.$		(3.379)

Na Figura 3.9, temos os gráficos da função seno e da reta tangente calculada no ponto $x=0$ .

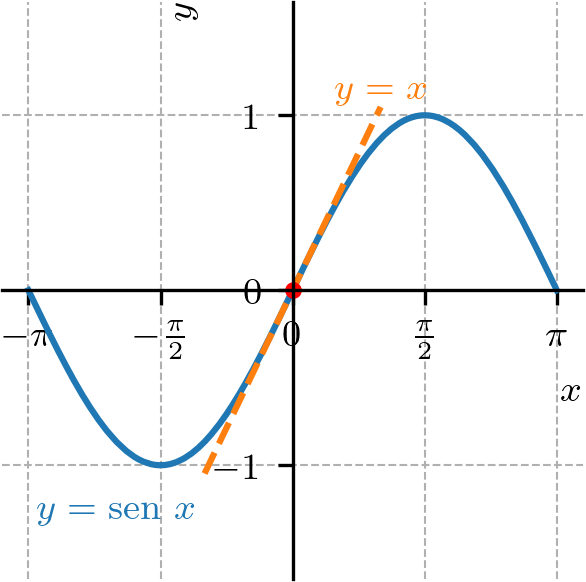Refer to caption — Figura 3.9: Gráficos da função seno e de sua reta tangente no ponto $x=0$ .

Código 64: Python

⬇

1from sympy import diff, sin, plot

2from sympy.abc import x

3f = lambda x: sin(x)

4x0 = 0

5# reta tangente

6rt = lambda x: diff(f(x),x).subs(x,x0)*(x-x0)+f(x).subs(x,x0)

7print("y =", rt(x))

8# graficos

9plot(f(x),rt(x),(x,-3.14,3.14))

ER 3.6.2.

Resolva a equação

\sec^{\prime}(x)=0,

(3.380)

para $x\in\left(\frac{\pi}{2},\frac{3\pi}{2}\right)$ .

Resolução.

Temos

	$\displaystyle 0=\sec^{\prime}(x)$		(3.381)
	$\displaystyle\text{}\quad=\sec(x)\operatorname{tg}(x)$		(3.382)
	$\displaystyle\text{}\quad=\frac{1}{\cos(x)}\frac{\operatorname{sen}(x)}{\cos(x)}$		(3.383)
	$\displaystyle\text{}\quad=\frac{\operatorname{sen}(x)}{\cos^{2}(x)}$		(3.384)

donde segue que

\operatorname{sen}(x)=0.

(3.385)

Por fim, observamos que para $x\in\left(\frac{\pi}{2},\frac{3\pi}{2}\right)$ , a função seno se anula somente em $x=\pi$ , a qual é a solução da equação.

3.6.3 Exercícios

E. 3.6.1.

Calcule a derivada em relação a $x$ de

a)

$\displaystyle f(x)=\operatorname{sen}(x)-\cos^{2}(x)$
b)

$\displaystyle g(x)=\operatorname{sen}^{2}(x)\cos(x)$
c)

$\displaystyle h(x)=\frac{2\operatorname{tg}(x)}{\sec(x)}$

a) $f^{\prime}(x)=\operatorname{sen}(2x)+\cos(x)$ ; b) $g^{\prime}(x)=\operatorname{sen}(x)\cdot(2-3\sin^{2}(x)))$ ; c) $h^{\prime}(x)=2\cos(x)$

E. 3.6.2.

Encontre a equação da reta tangente ao gráfico da função $y=\cos x$ no ponto $x=0$ . Então, faça os esboços desta função e da reta tangente, em uma mesma figura.

$y=1$ . Dica: use um pacote de matemática simbólica para verificar os esboços dos gráficos.

E. 3.6.3.

Calcule a derivada em relação a $x$ de

a)

$\displaystyle f(x)=\operatorname{tg}(x)-\operatorname{cotg}(x)$
b)

$\displaystyle g(x)=\sec(x)-\operatorname{cossec}(x)$
c)

$\displaystyle h(x)=\frac{\operatorname{sen}(x)}{2\cos(x)}$

a) $f^{\prime}(x)=\sec^{2}(x)+\operatorname{cossec}^{2}(x)$ ; b) $g^{\prime}(x)=\sec(x)\operatorname{tg}(x)+\operatorname{cossec}(x)% \operatorname{cotg}(x)$ ; c) $h^{\prime}(x)=\frac{1}{2}\sec^{2}(x)$

E. 3.6.4.

Mostre que $\displaystyle(\operatorname{cotg}x)^{\prime}=-\operatorname{cossec}^{2}(x)$ .

	$\displaystyle\operatorname{cotg}^{\prime}x=\left(\frac{\cos x}{\operatorname{% sen}x}\right)^{\prime}$
	$\displaystyle\text{}\quad=-\operatorname{cossec}^{2}x$

E. 3.6.5.

Mostre que $\displaystyle(\operatorname{cossec}x)^{\prime}=-\operatorname{cotg}x% \operatorname{cossec}x$ .

	$\displaystyle\operatorname{cossec}^{\prime}x=\left(\frac{1}{\operatorname{sen}% x}\right)^{\prime}$
	$\displaystyle\text{}\quad=-\operatorname{cotg}x\operatorname{cossec}x$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Cálculo I

3.6 Derivadas de funções trigonométricas

Exemplo 3.6.1.

Observação 3.6.1.

Exemplo 3.6.2.

3.6.1 Lista de derivadas

3.6.2 Exercícios resolvidos

ER 3.6.1.

Resolução.

ER 3.6.2.

Resolução.

3.6.3 Exercícios

E. 3.6.1.

E. 3.6.2.

E. 3.6.3.

E. 3.6.4.

E. 3.6.5.

Envie seu comentário

	$\displaystyle\sec^{\prime}x=\left(\frac{1}{\cos x}\right)^{\prime}$		(3.348)
	$\displaystyle\text{}\quad=\frac{-\cos^{\prime}x}{\cos^{2}x}$		(3.349)
	$\displaystyle\text{}\quad=\frac{\operatorname{sen}x}{\cos^{2}x}$		(3.350)
	$\displaystyle\text{}\quad=\frac{\operatorname{sen}x}{\cos x}\cdot\frac{1}{\cos x}$		(3.351)
	$\displaystyle\text{}\quad=\operatorname{tg}x\sec x.$		(3.352)