Cálculo I

3 Derivadas 3.6 Derivadas de funções trigonométricas 3.8 Regra da cadeia

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.7 Linearização e diferenciais

Uma função diferenciável em um ponto $x_{0}$ pode ser aproximada pela reta tangente ao seu gráfico neste ponto. Esta aproximação é chamada de linearização da função em $x_{0}$ . Este fato, também pode ser usado para aproximar o valor da função em pontos próximos a $x_{0}$ , através do conceito de diferencial.

3.7.1 Linearização

Se $f$ é diferenciável em $x_{0}$ , então a linearização de $f$ em $x_{0}$ é a função

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}l(x)=f^{% \prime}(x_{0})(x-x_{0})+f(x_{0}).

(3.388)

Trata-se de uma aproximação linear de $f$ em torno de $x_{0}$ , i.e. $f(x)\approx l(x)$ para $x$ próximo de $x_{0}$ . Consultemos a Figura 3.10.

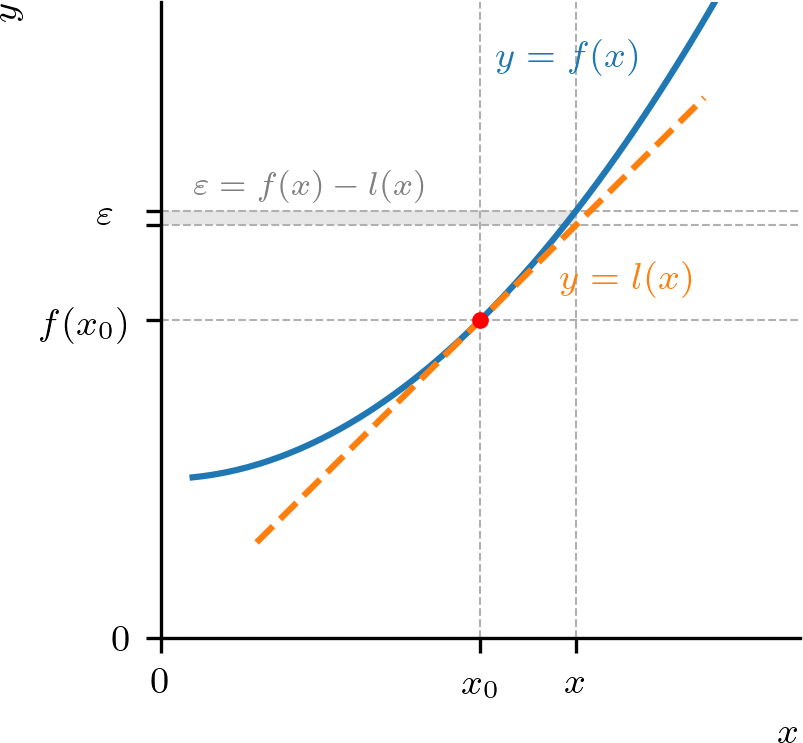
Refer to caption — Figura 3.10: Gráficos de $f$ e sua linearização $l$ em $x_{0}$ .

Observemos que o gráfico de $l$ é a reta tangente ao gráfico de $f$ no ponto $(x_{0},f(x_{0}))$ . Podemos usar a linearização para aproximar o valor de $f$ em pontos próximos a $x_{0}$ , temos

f(x)=l(x)+\varepsilon,

(3.389)

onde $\varepsilon=\varepsilon(|x-x_{0}|)$ é um erro que tende a zero quando $x$ tende a $x_{0}$ .

Exemplo 3.7.1.

Temos que $\ln(1+x)\approx x$ para $x$ próximo de $0$ . Isto é consequência da linearização de $f(x)=\ln(1+x)$ em $x_{0}=0$ , pois

	$\displaystyle f^{\prime}(x)=\frac{1}{1+x}$		(3.390)
	$\displaystyle f^{\prime}(0)=1$		(3.391)
	$\displaystyle f(0)=\ln(1+0)=0.$		(3.392)

Logo, a linearização de $f$ em $x_{0}=0$ é

	$\displaystyle l(x)=f^{\prime}(x_{0})(x-x_{0})+f(x_{0})$		(3.393)
	$\displaystyle\text{}\quad=1\cdot(x-0)+0=x.$		(3.394)

A seguinte tabela contém o erro desta aproximação, i.e. $\varepsilon=|l(x)-f(x)|$ para alguns valores de $x$ próximos de $0$ .

$x$	$\ln(1+x)$	$l(x)$	$\varepsilon$
$1.0$	$0.6931$	$1.0$	$0.3068$
$0.5$	$0.4055$	$0.5$	$0.0945$
$0.1$	$0.0953$	$0.1$	$0.0047$

Código 35: Python

⬇

1from sympy import Symbol, ln, diff, Lambda

2x = Symbol('x')

3f = Lambda(x, ln(x+1))

4print(f'f(x) = {f(x)}')

5fl = Lambda(x, diff(f(x), x))

6x0 = 0

7l = Lambda(x, fl(x0)*(x-x0) + f(x0))

8print(f'l(x) = {l(x)}')

f(x) = log(x + 1)

l(x) = x

3.7.2 Diferenciais

Se $y=f(x)$ é uma função diferenciável em $x$ , então definimos a diferencial de $y$ como sendo

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\mathrm{d}y=f% ^{\prime}(x)\mathrm{d}x,

(3.395)

onde $\mathrm{d}x$ é a diferencial de $x$ , i.e. uma variação infenitesimal de $x$ . A diferencial $\mathrm{d}y$ é uma aproximação da variação de $y$ quando $x$ varia de $x$ para $x+\mathrm{d}x$ . Esta é uma consequência da linearização de $f$ em $x$ , pois

	$\displaystyle f(x+\mathrm{d}x)\approx L(x+\mathrm{d}x)$		(3.396)
	$\displaystyle\text{}\quad=f^{\prime}(x)(x+\mathrm{d}x-x)+f(x)$		(3.397)
	$\displaystyle\text{}\quad=f^{\prime}(x)\mathrm{d}x+f(x),$		(3.398)

onde segue que

f(x+\mathrm{d}x)-f(x)\approx f^{\prime}(x)\mathrm{d}x,

(3.400)

i.e. a variação de $y$ é aproximadamente igual a diferencial $\mathrm{d}y$ . A relação entre as diferenciais motiva a notação de Leibniz¹¹¹¹endnote: ¹¹Gottfried Wilhelm Leibniz, 1646 - 1716, matemático e filósofo alemão. Fonte: Wikipédia: Gottfried Wilhelm Leibniz., onde

\frac{\mathrm{d}y}{\mathrm{d}x}=f^{\prime}(x).

(3.401)

Exemplo 3.7.2.

Seja $C$ o comprimento de uma círcunferência de raio $r$ . Sabemos que $C=2\pi r$ . Usando de diferenciais, podemos estimar a variação de $A$ quando $r$ varia de $5$ m para $5.5$ m. Calculamos

	$\displaystyle\mathrm{d}C=(2\pi r)^{\prime}\mathrm{d}r$		(3.402)
	$\displaystyle\text{}\quad=2\pi\mathrm{d}r.$		(3.403)

Assim sendo, para $\mathrm{d}r=0.5$ m, temos

\mathrm{d}C=2\pi\cdot 0.5=\pi\text{m}\approx 3.14\text{m}.

(3.404)

Ou seja, quando o raio varia de $5$ m para $5.5$ m, o comprimento da circunferência varia aproximadamente $3.14$ m.

Notemos que a variação exata do comprimento é

	$\displaystyle\Delta C=C(5.5)-C(5)$		(3.405)
	$\displaystyle\text{}\quad=2\pi\cdot 5.5-2\pi\cdot 5$		(3.406)
	$\displaystyle\text{}\quad=2\pi\cdot 0.5=\pi\text{m}\approx 3.14\text{m}.$		(3.407)

Ou seja, neste caso, a aproximação pela diferencial é exata.

Exemplo 3.7.3.

Seja $V=x^{3}$ o volume de um cubo de aresta $x$ . Usando de diferenciais, podemos estimar a variação de $V$ quando $x$ varia de $2$ m para $2.1$ m. Calculamos

	$\displaystyle\mathrm{d}V=(x^{3})^{\prime}\mathrm{d}x$		(3.408)
	$\displaystyle\text{}\quad=3x^{2}\mathrm{d}x.$		(3.409)

Assim sendo, para $x=2$ m e $\mathrm{d}x=0.1$ m, temos

\mathrm{d}V=3\cdot 2^{2}\cdot 0.1=1.2\text{m}^{3}.

(3.410)

Ou seja, quando a aresta varia de $2$ m para $2.1$ m, o volume do cubo varia aproximadamente $1.2\text{m}^{3}$ . Qual é o erro desta aproximação? Verifique!

3.7.3 Exercícios resolvidos

ER 3.7.1.

Use a linearização para aproximar o valor de $\sqrt{4.1}$ .

Resolução.

Seja $f(x)=\sqrt{x}$ . Podemos aproximá-la por sua linearização $l(x)$ em $x_{0}=4$ . Para tanto, calculamos

	$\displaystyle f^{\prime}(x)=\left(x^{\frac{1}{2}}\right)^{\prime}$		(3.411)
	$\displaystyle\text{}\quad=\frac{1}{2}x^{-\frac{1}{2}}=\frac{1}{2\sqrt{x}}$		(3.412)
	$\displaystyle f^{\prime}(4)=\frac{1}{2\sqrt{4}}=\frac{1}{4}$		(3.413)
	$\displaystyle f(4)=\sqrt{4}=2.$		(3.414)

Logo, a linearização de $f$ em $x_{0}=4$ é

	$\displaystyle l(x)=f^{\prime}(x_{0})(x-x_{0})+f(x_{0})$		(3.415)
	$\displaystyle\text{}\quad=\frac{1}{4}(x-4)+2$		(3.416)
	$\displaystyle\text{}\quad=\frac{x}{4}+1.$		(3.417)

Assim sendo, para $x=4.1$ , temos

	$\displaystyle\sqrt{4.1}=f(4.1)\approx l(4.1)$		(3.418)
	$\displaystyle\text{}\quad=\frac{4.1}{4}+1=2.025.$		(3.419)

O valor exato é $\sqrt{4.1}\approx 2.02485$ , i.e. o erro da aproximação é aproximadamente $0.00015$ .

ER 3.7.2.

Use de diferenciais para estimar a variação da área de um círculo quando seu raio varia de $5$ cm para $5.1$ cm. Então, verifique o erro desta aproximação.

Resolução.

Seja $A=\pi r^{2}$ a área de um círculo de raio $r$ . Usando de diferenciais, podemos estimar a variação de $A$ quando $r$ varia de $5$ cm para $5.1$ cm. Calculamos

	$\displaystyle\mathrm{d}A=(\pi r^{2})^{\prime}\mathrm{d}r$		(3.420)
	$\displaystyle\text{}\quad=2\pi r\mathrm{d}r.$		(3.421)

Assim sendo, para $r=5$ cm e $\mathrm{d}r=0.1$ cm, temos

	$\displaystyle\mathrm{d}A=2\pi\cdot 5\cdot 0.1$		(3.422)
	$\displaystyle\text{}\quad=\pi\text{cm}^{2}\approx 3.14\text{cm}^{2}.$		(3.423)

Ou seja, quando o raio varia de $5$ cm para $5.1$ cm, a área do círculo varia aproximadamente $3.14\text{cm}^{2}$ .

O erro desta aproximação é

	$\displaystyle\varepsilon=\|\Delta A-\mathrm{d}A\|$		(3.424)
	$\displaystyle\text{}\quad=\|\pi(5.1)^{2}-\pi(5)^{2}-\pi\|$		(3.425)
	$\displaystyle\text{}\quad=\|\pi(26.01-25-1)\|$		(3.426)
	$\displaystyle\text{}\quad=\|\pi(0.01)\|$		(3.427)
	$\displaystyle\text{}\quad=0.01\pi\text{cm}^{2}\approx 0.0314\text{cm}^{2}.$		(3.428)

Erro na aproximação diferencial

Seja $f$ uma função diferenciável em $x$ . A aproximação da variação de $f$ pela diferencial é dada por

	$\displaystyle\Delta y=f(x+\Delta x)-f(x)$		(3.429)
	$\displaystyle\text{}\quad\approx\mathrm{d}y=f^{\prime}(x)\Delta x,$		(3.430)

onde $\Delta x$ é uma variação finita de $x$ e $\mathrm{d}x$ é uma variação infinitesimal de $x$ . O erro desta aproximação é

	$\displaystyle\Delta y-\mathrm{d}y=f(x+\Delta x)-f(x)-f^{\prime}(x)\Delta x.$		(3.431)
	$\displaystyle\text{}\quad=\underbrace{\left(\frac{f(x+\Delta x)-f(x)}{\Delta x% }-f^{\prime}(x)\right)}_{\varepsilon}\Delta x.$		(3.432)

Com isso, podemos escrever

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\Delta y=f^{% \prime}(x)\Delta x+\varepsilon\Delta x,

(3.433)

em que $\varepsilon\to 0$ quando $\Delta x\to 0$ .

3.7.4 Exercícios

E. 3.7.1.

Calcule a linearização de $f(x)=\sqrt{1+x}$ em $x_{0}=0$ . Então, use-a para aproximar o valor de $\sqrt{1.1}$ .

$l(x)=\frac{x}{2}+1$ , $l(0.1)=1.05$ .

E. 3.7.2.

Qual é a linearização de $y=\operatorname{sen}(x)$ em $x=0$ . Então, use-a para aproximar o valor de $\operatorname{sen}(0.1)$ .

$l(x)=x$ , $l(0.1)=0.1$ .

E. 3.7.3.

Mostre que valem as seguintes aproximações para $x$ próximo de $0$ :

a)

$\cos x\approx 1$
b)

$\operatorname{tg}x\approx x$
c)

$e^{x}\approx 1+x$
d)

$\ln(1+x)\approx x$

Basta calcular as linearizações de cada função em $x_{0}=0$ : a) $l(x)=1$ ; b) $l(x)=x$ ; c) $l(x)=1+x$ ; d) $l(x)=x$ .

E. 3.7.4.

Mostre que $(1+x)^{k}\approx 1+kx$ para $x$ próximo de $0$ .

Basta calcular a linearização de $f(x)=(1+x)^{k}$ em $x_{0}=0$ : $l(x)=kx+1$ .

E. 3.7.5.

Lembrando-se que o volume de uma esfera de raio $r$ é $V=\frac{4}{3}\pi r^{3}$ , use de diferenciais para estimar a variação do volume quando o raio varia de $10$ cm para $10.1$ cm. Então, verifique o erro desta aproximação.

A variação aproximada do volume é $40\pi\text{cm}^{3}$ . O erro desta aproximação é aproximadamente $0.4\text{cm}^{3}$ .

E. 3.7.6.

Lembrando-se que a área da superfície de uma esfera de raio $r$ é $A=4\pi r^{2}$ , use de diferenciais para estimar a variação da área quando o raio varia de $10$ cm para $10.1$ cm.

A variação aproximada da área é $8\pi\text{cm}^{2}$ .

E. 3.7.7.

Use de diferenciais para estimar a variação da área de superfície de um cubo quando sua aresta varia de $2$ m para $2.05$ m. Então, verifique o erro desta aproximação.

A variação aproximada da área é $1.2\text{m}^{2}$ . O erro desta aproximação é aproximadamente $0.2025\text{m}^{2}$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Cálculo I

3.7 Linearização e diferenciais

3.7.1 Linearização

Exemplo 3.7.1.

3.7.2 Diferenciais

Exemplo 3.7.2.

Exemplo 3.7.3.

3.7.3 Exercícios resolvidos

ER 3.7.1.

Resolução.

ER 3.7.2.

Resolução.

Erro na aproximação diferencial

3.7.4 Exercícios

E. 3.7.1.

E. 3.7.2.

E. 3.7.3.

E. 3.7.4.

E. 3.7.5.

E. 3.7.6.

E. 3.7.7.

Envie seu comentário