Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.3 Bases e Coordenadas
Seja o conjunto de todos os vetores no espaço tridimensional. Conforme discutido na Seção 2.2, se , e são l.i., então qualquer vetor pode ser escrito como uma combinação linear destes vetores, i.e. existem escalares , e tal que
| (2.49) |
Isso motiva a seguinte definição: uma base de é uma sequência de três vetores l.i. de .
A seguinte proposição vai nos fornecer a noção de coordenadas no espaço.
Proposição 2.3.1.
Seja uma base de . Então, dado qualquer , existe uma única tripla de escalares tais que
| (2.50) |
Demonstração.
A existência dos escalares , e segue imediatamente do fato de que , e são l.i. e, portanto, pode ser escrito como uma combinação linear destes vetores (Consulte a Subseção 2.2.3).
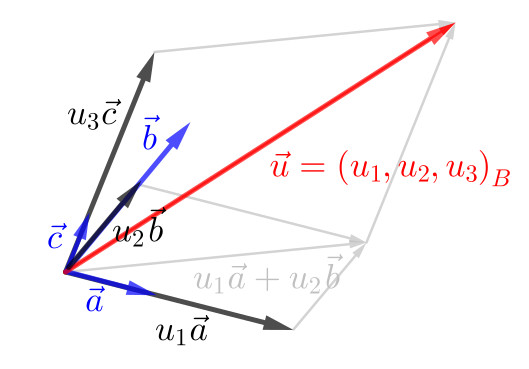
Desta última proposição, fixada uma base , cada vetor é representado de forma única como combinação linear dos vetores da base, digamos
| (2.54) |
onde a sequência de escalares é chamada de coordenadas do vetor na base e escrevemos
| (2.55) |
para expressar o vetor nas suas coordenadas na base . Consulte a Figura 2.7.
Exemplo 2.3.1.
Fixada uma base , o vetor de coordenadas
| (2.56) |
é o vetor
| (2.57) |
2.3.1 Operações de Vetores com Coordenadas
Na Seção 1.2, definimos as operações de adição, subtração e multiplicação por escalar do ponto de vista geométrico. Aqui, estudamos como estas operações são definidas a partir das coordenadas de vetores.
A partir daqui, assumimos dada uma base de vetores .
Adição
Dados vetores e , i.e.
| (2.58) | ||||
| (2.59) |
a adição de com é a soma
| (2.60) | ||||
| (2.61) |
Ou seja,
| (2.62) |
Exemplo 2.3.2.
A adição do vetor
| (2.63) |
com o vetor
| (2.64) |
resulta no vetor
| (2.65) | ||||
| (2.66) |
Vetor Oposto
O vetor oposto ao vetor é
| (2.67) | ||||
| (2.68) |
ou seja,
| (2.69) |
Exemplo 2.3.3.
Dado o vetor , temos
| (2.70) |
Subtração de Vetores
Lembrando que subtração de com é definida por
| (2.71) |
temos que
| (2.72) | ||||
| (2.73) | ||||
| (2.74) | ||||
| (2.75) |
Em resumo, a subtração de com é o vetor
| (2.76) |
Exemplo 2.3.4.
Sejam os vetores
| (2.77) |
e
| (2.78) |
temos que
| (2.79) | ||||
| (2.80) |
Multiplicação por Escalar
Dado um escalar e um vetor , temos a multiplicação por escalar
| (2.81) | ||||
| (2.82) |
ou seja,
| (2.83) |
Exemplo 2.3.5.
Dado o vetor , temos
| (2.84) | ||||
| (2.85) | ||||
| (2.86) |
2.3.2 Dependência linear
Vamos estudar como podemos analisar a dependência linear de vetores a partir de suas coordenadas. Assumimos fixada uma base .
Dois vetores
Na Proposição 2.2.1, provamos que dois vetores , são linearmente dependentes (l.d.) se, e somente se, um for múltiplo do outro, i.e. existe um número real tal que
| (2.87) |
sem perda de generalidade99endnote: 9Formalmente, pode ocorrer .. Em coordenadas, temos
| (2.88) | ||||
| (2.89) |
donde
| (2.90) | ||||
| (2.91) | ||||
| (2.92) |
Concluímos que dois vetores são l.d. se, e somente se, as coordenadas de um deles forem, respectivamente, múltiplas (de mesmo fator) das coordenadas do outro.
Exemplo 2.3.6.
Estudamos os seguintes casos:
-
a)
Dois vetores l.d..
Sejam
(2.93) e
(2.94) Ao buscarmos por um escalar tal que
(2.95) temos
(2.96) (2.97) donde segue que
(2.98) (2.99) (2.100) Concluímos que , logo e são l.d..
-
b)
Dois vetores l.i..
Sejam, agora, os vetores
(2.101) e
(2.102) Buscando por tal que
(2.103) chegamos no sistema de equações
(2.104) que não tem solução. De fato, na primeira equação , mas na segunda , logo não existe tal que . Concluímos que e são l.i..
Três Vetores
Na Subseção 2.2.2, estudamos que três vetores , e são linearmente independentes (l.i.), quando
| (2.105) | ||||
Assumimos fixada uma base no espaço. Então, temos que
| (2.106) |
é equivalente a
| (2.107) |
ou, ainda,
| (2.108) |
Esta, por sua vez, nos leva ao seguinte sistema linear
| (2.109) |
Agora, lembremos que um tal sistema tem solução única1010endnote: 10Neste caso, a solução trivial se, e somente se, o determinante de sua matriz dos coeficientes é não nulo, i.e.
| (2.110) |
Neste caso, concluímos que é um conjunto de vetores l.i. e, noutro caso, é l.d..
Exemplo 2.3.7.
Os vetores
| (2.111) |
formam um conjunto l.d., pois
| (2.112) | ||||
| (2.113) | ||||
| (2.114) |
2.3.3 Bases Ortonormais
Uma base é dita ser ortonormal1111endnote: 11Quando ortogonal a , denotamos ., quando
-
•
, e são dois a dois ortogonais, e
-
•
.
Lema 2.3.1.
(Pitágoras1212endnote: 12Pitágoras de Samos, c.570, c. 495 a.C., matemático grego jônico. Fonte: Wikipédia:Pitágoras..) Se , então
| (2.115) |
Demonstração.
Consulte o E.2.3.7. ∎
Proposição 2.3.2.
Seja uma base ortonormal e . Então,
| (2.116) |
Demonstração.
Temos . Seja um plano determinado por dadas representações de e . Como , e são ortogonais, temos que é ortogonal ao plano . Além disso, o vetor também admite uma representação em , logo é ortogonal a . Do Lema 12, temos
| (2.117) |
Analogamente, como , temos
| (2.118) | ||||
| (2.119) | ||||
| (2.120) |
Extraindo a raiz quadrada de ambos os lados da última equação, obtemos o resultado desejado. ∎
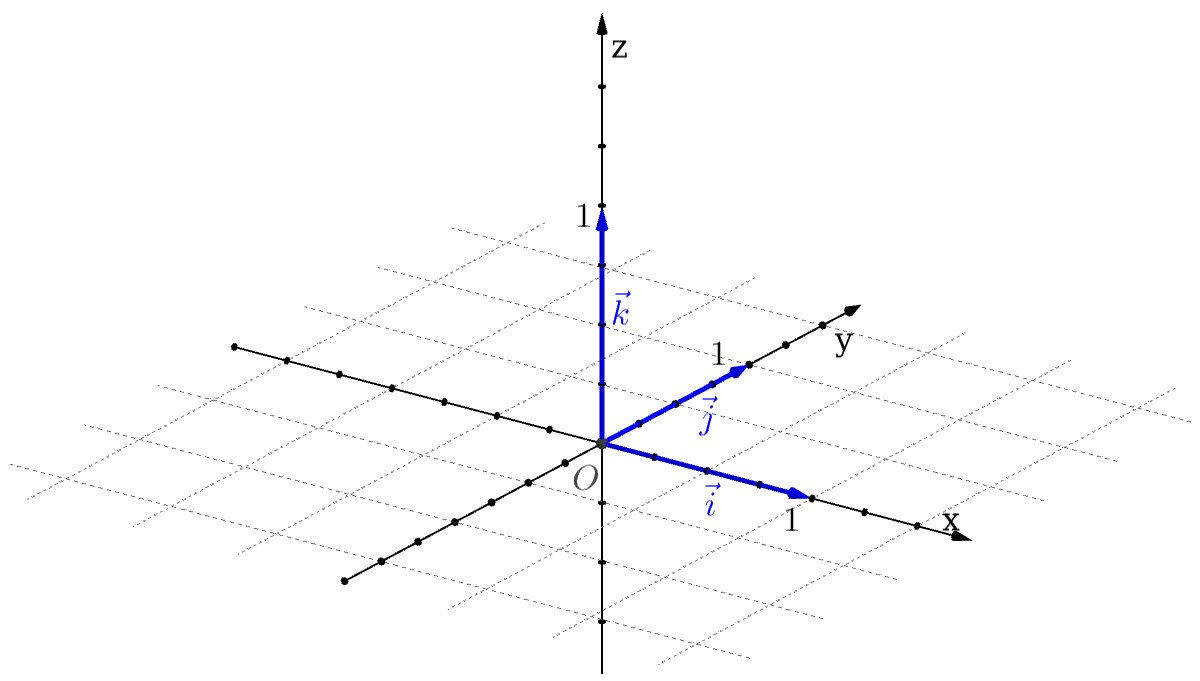
A partir daqui, salvo dito o contrário, vamos assumir fixada uma base ortonormal e, por simplicidade, escrevemos
| (2.121) | ||||
| (2.122) |
Exemplo 2.3.8.
A norma de é
| (2.123) | ||||
| (2.124) |
2.3.4 Exercícios Resolvidos
ER 2.3.1.
Considere a base ortonormal conforme dada na Figura 2.8. Faça uma representação do vetor
| (2.125) |
Solução 0.
Primeiramente, observamos que
| (2.126) | ||||
| (2.127) |
Assim sendo, podemos construir uma representação de como dada na figura abaixo. Primeiramente, representamos os vetores e (cinza). Então, representamos o vetor (cinza). Por fim, temos a representação de (vermelho).
![[Uncaptioned image]](cap_base/dados/fig_exeresol_base/fig.jpg)
ER 2.3.2.
Fixada uma base qualquer e dados e , encontre o vetor que satisfaça
| (2.128) |
Solução 0.
Primeiramente, podemos manipular a equação de forma a isolarmos como segue
| (2.129) | |||
| (2.130) | |||
| (2.131) | |||
| (2.132) |
Agora, sabendo que e , temos
| (2.133) | |||
| (2.134) | |||
| (2.135) | |||
| (2.136) |
ER 2.3.3.
Fixada uma base qualquer, verifique se os vetores , e também formam um base para o espaço de vetores.
Solução 0.
Uma base para o espaço tridimensional é uma sequência de três vetores l.i.. Logo, para resolver a questão, basta verificar se é l.i.. Com base na Subseção 2.3.2, basta calcularmos o determinante da matriz cujas colunas são formadas pelas coordenadas dos vetores da sequência, i.e.
| (2.137) | |||
| (2.138) | |||
| (2.139) | |||
| (2.140) |
Como este determinante é nulo, concluímos que é l.d. e, portanto, não forma uma base para .
2.3.5 Exercícios
E. 2.3.1.
Considere a base conforme dada na Figura 2.8. Faça um esboço do vetor .
E. 2.3.2.
Fixada uma base e sabendo que , escreva como combinação linear de , e .
Resposta 0.
E. 2.3.3.
Fixada uma base qualquer e , e , calcule:
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) ; b) ; c) ; d)
E. 2.3.4.
Faxada uma base qualquer, verifique se os seguintes conjuntos de vetores são l.i. ou l.d..
-
a)
,
-
b)
,
-
c)
,
-
d)
,
-
e)
,
-
f)
,
Resposta 0.
a) l.i.; b) l.i.; c) l.d.; d) l.i.; e) l.i.; f) l.d.
E. 2.3.5.
Faxada uma base qualquer, verifique se os seguintes conjuntos de vetores são l.i. ou l.d..
-
a)
, ,
-
b)
, ,
-
c)
, ,
Resposta 0.
a) l.i.; b) l.i.; c) l.d.
E. 2.3.6.
Seja uma base ortogonal, i.e. , e são l.i. e dois a dois ortogonais. Mostre que é uma base ortonormal.
Resposta 0.
Segue imediatamente do fato de que para qualquer vetor .
E. 2.3.7.
Demostre o Lema 12.
Resposta 0.
![[Uncaptioned image]](cap_base/dados/fig_pitagoras/fig.jpg)
Sejam as representações , e, portanto, . Como , temos que o triângulo é retângulo e, pelo Teorema de Pitágoras, segue que . Logo, .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.3 Bases e Coordenadas
Seja o conjunto de todos os vetores no espaço tridimensional. Conforme discutido na Seção 2.2, se , e são l.i., então qualquer vetor pode ser escrito como uma combinação linear destes vetores, i.e. existem escalares , e tal que
| (2.49) |
Isso motiva a seguinte definição: uma base de é uma sequência de três vetores l.i. de .
A seguinte proposição vai nos fornecer a noção de coordenadas no espaço.
Proposição 2.3.1.
Seja uma base de . Então, dado qualquer , existe uma única tripla de escalares tais que
| (2.50) |
Demonstração.
A existência dos escalares , e segue imediatamente do fato de que , e são l.i. e, portanto, pode ser escrito como uma combinação linear destes vetores (Consulte a Subseção 2.2.3).

Desta última proposição, fixada uma base , cada vetor é representado de forma única como combinação linear dos vetores da base, digamos
| (2.54) |
onde a sequência de escalares é chamada de coordenadas do vetor na base e escrevemos
| (2.55) |
para expressar o vetor nas suas coordenadas na base . Consulte a Figura 2.7.
Exemplo 2.3.1.
Fixada uma base , o vetor de coordenadas
| (2.56) |
é o vetor
| (2.57) |
2.3.1 Operações de Vetores com Coordenadas
Na Seção 1.2, definimos as operações de adição, subtração e multiplicação por escalar do ponto de vista geométrico. Aqui, estudamos como estas operações são definidas a partir das coordenadas de vetores.
A partir daqui, assumimos dada uma base de vetores .
Adição
Dados vetores e , i.e.
| (2.58) | ||||
| (2.59) |
a adição de com é a soma
| (2.60) | ||||
| (2.61) |
Ou seja,
| (2.62) |
Exemplo 2.3.2.
A adição do vetor
| (2.63) |
com o vetor
| (2.64) |
resulta no vetor
| (2.65) | ||||
| (2.66) |
Vetor Oposto
O vetor oposto ao vetor é
| (2.67) | ||||
| (2.68) |
ou seja,
| (2.69) |
Exemplo 2.3.3.
Dado o vetor , temos
| (2.70) |
Subtração de Vetores
Lembrando que subtração de com é definida por
| (2.71) |
temos que
| (2.72) | ||||
| (2.73) | ||||
| (2.74) | ||||
| (2.75) |
Em resumo, a subtração de com é o vetor
| (2.76) |
Exemplo 2.3.4.
Sejam os vetores
| (2.77) |
e
| (2.78) |
temos que
| (2.79) | ||||
| (2.80) |
Multiplicação por Escalar
Dado um escalar e um vetor , temos a multiplicação por escalar
| (2.81) | ||||
| (2.82) |
ou seja,
| (2.83) |
Exemplo 2.3.5.
Dado o vetor , temos
| (2.84) | ||||
| (2.85) | ||||
| (2.86) |
2.3.2 Dependência linear
Vamos estudar como podemos analisar a dependência linear de vetores a partir de suas coordenadas. Assumimos fixada uma base .
Dois vetores
Na Proposição 2.2.1, provamos que dois vetores , são linearmente dependentes (l.d.) se, e somente se, um for múltiplo do outro, i.e. existe um número real tal que
| (2.87) |
sem perda de generalidade99endnote: 9Formalmente, pode ocorrer .. Em coordenadas, temos
| (2.88) | ||||
| (2.89) |
donde
| (2.90) | ||||
| (2.91) | ||||
| (2.92) |
Concluímos que dois vetores são l.d. se, e somente se, as coordenadas de um deles forem, respectivamente, múltiplas (de mesmo fator) das coordenadas do outro.
Exemplo 2.3.6.
Estudamos os seguintes casos:
-
a)
Dois vetores l.d..
Sejam
(2.93) e
(2.94) Ao buscarmos por um escalar tal que
(2.95) temos
(2.96) (2.97) donde segue que
(2.98) (2.99) (2.100) Concluímos que , logo e são l.d..
-
b)
Dois vetores l.i..
Sejam, agora, os vetores
(2.101) e
(2.102) Buscando por tal que
(2.103) chegamos no sistema de equações
(2.104) que não tem solução. De fato, na primeira equação , mas na segunda , logo não existe tal que . Concluímos que e são l.i..
Três Vetores
Na Subseção 2.2.2, estudamos que três vetores , e são linearmente independentes (l.i.), quando
| (2.105) | ||||
Assumimos fixada uma base no espaço. Então, temos que
| (2.106) |
é equivalente a
| (2.107) |
ou, ainda,
| (2.108) |
Esta, por sua vez, nos leva ao seguinte sistema linear
| (2.109) |
Agora, lembremos que um tal sistema tem solução única1010endnote: 10Neste caso, a solução trivial se, e somente se, o determinante de sua matriz dos coeficientes é não nulo, i.e.
| (2.110) |
Neste caso, concluímos que é um conjunto de vetores l.i. e, noutro caso, é l.d..
Exemplo 2.3.7.
Os vetores
| (2.111) |
formam um conjunto l.d., pois
| (2.112) | ||||
| (2.113) | ||||
| (2.114) |
2.3.3 Bases Ortonormais
Uma base é dita ser ortonormal1111endnote: 11Quando ortogonal a , denotamos ., quando
-
•
, e são dois a dois ortogonais, e
-
•
.

Lema 2.3.1.
(Pitágoras1212endnote: 12Pitágoras de Samos, c.570, c. 495 a.C., matemático grego jônico. Fonte: Wikipédia:Pitágoras..) Se , então
| (2.115) |
Demonstração.
Consulte o E.2.3.7. ∎
Proposição 2.3.2.
Seja uma base ortonormal e . Então,
| (2.116) |
Demonstração.
Temos . Seja um plano determinado por dadas representações de e . Como , e são ortogonais, temos que é ortogonal ao plano . Além disso, o vetor também admite uma representação em , logo é ortogonal a . Do Lema 12, temos
| (2.117) |
Analogamente, como , temos
| (2.118) | ||||
| (2.119) | ||||
| (2.120) |
Extraindo a raiz quadrada de ambos os lados da última equação, obtemos o resultado desejado. ∎
A partir daqui, salvo dito o contrário, vamos assumir fixada uma base ortonormal e, por simplicidade, escrevemos
| (2.121) | ||||
| (2.122) |
Exemplo 2.3.8.
A norma de é
| (2.123) | ||||
| (2.124) |
2.3.4 Exercícios Resolvidos
ER 2.3.1.
Considere a base ortonormal conforme dada na Figura 2.8. Faça uma representação do vetor
| (2.125) |
Solução 0.
Primeiramente, observamos que
| (2.126) | ||||
| (2.127) |
Assim sendo, podemos construir uma representação de como dada na figura abaixo. Primeiramente, representamos os vetores e (cinza). Então, representamos o vetor (cinza). Por fim, temos a representação de (vermelho).
![[Uncaptioned image]](cap_base/dados/fig_exeresol_base/fig.jpg)
ER 2.3.2.
Fixada uma base qualquer e dados e , encontre o vetor que satisfaça
| (2.128) |
Solução 0.
Primeiramente, podemos manipular a equação de forma a isolarmos como segue
| (2.129) | |||
| (2.130) | |||
| (2.131) | |||
| (2.132) |
Agora, sabendo que e , temos
| (2.133) | |||
| (2.134) | |||
| (2.135) | |||
| (2.136) |
ER 2.3.3.
Fixada uma base qualquer, verifique se os vetores , e também formam um base para o espaço de vetores.
Solução 0.
Uma base para o espaço tridimensional é uma sequência de três vetores l.i.. Logo, para resolver a questão, basta verificar se é l.i.. Com base na Subseção 2.3.2, basta calcularmos o determinante da matriz cujas colunas são formadas pelas coordenadas dos vetores da sequência, i.e.
| (2.137) | |||
| (2.138) | |||
| (2.139) | |||
| (2.140) |
Como este determinante é nulo, concluímos que é l.d. e, portanto, não forma uma base para .
2.3.5 Exercícios
E. 2.3.1.
Considere a base conforme dada na Figura 2.8. Faça um esboço do vetor .
E. 2.3.2.
Fixada uma base e sabendo que , escreva como combinação linear de , e .
Resposta 0.
E. 2.3.3.
Fixada uma base qualquer e , e , calcule:
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) ; b) ; c) ; d)
E. 2.3.4.
Faxada uma base qualquer, verifique se os seguintes conjuntos de vetores são l.i. ou l.d..
-
a)
,
-
b)
,
-
c)
,
-
d)
,
-
e)
,
-
f)
,
Resposta 0.
a) l.i.; b) l.i.; c) l.d.; d) l.i.; e) l.i.; f) l.d.
E. 2.3.5.
Faxada uma base qualquer, verifique se os seguintes conjuntos de vetores são l.i. ou l.d..
-
a)
, ,
-
b)
, ,
-
c)
, ,
Resposta 0.
a) l.i.; b) l.i.; c) l.d.
E. 2.3.6.
Seja uma base ortogonal, i.e. , e são l.i. e dois a dois ortogonais. Mostre que é uma base ortonormal.
Resposta 0.
Segue imediatamente do fato de que para qualquer vetor .
E. 2.3.7.
Demostre o Lema 12.
Resposta 0.
![[Uncaptioned image]](cap_base/dados/fig_pitagoras/fig.jpg)
Sejam as representações , e, portanto, . Como , temos que o triângulo é retângulo e, pelo Teorema de Pitágoras, segue que . Logo, .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.