Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.2 Dependência Linear
Dois ou mais vetores dados são linearmente dependentes (l.d.) quando um deles for combinação linear dos demais. Mais precisamente, é um conjunto de vetores l.d. quando
| (2.23) |
para escalares não todos nulos. Caso contrário, dizemos tratar-se de um conjunto de vetores linearmente independentes (l.i.).
Exemplo 2.2.1.
Estudamos cada caso:
-
a)
Sejam e . Temos que e são linearmente dependentes, pois
(2.24) -
b)
Sejam , e . Temos que é um conjunto l.d., pois
(2.25)
Observação 2.2.1.
(Vetor Nulo.) Todo conjunto de vetores que contenha o vetor nulo é um conjunto l.d.. De fato, para quaisquer , , …, , tem-se que
| (2.26) |
2.2.1 Dois Vetores no Espaço
Dois vetores de mesma direção são linearmente dependentes (l.d.).
Proposição 2.2.1.
Dois vetores não nulos e são l.d. se, e somente se, qualquer uma das seguinte condições é satisfeita:
-
a)
um deles é combinação linear do outro, i.e.
(2.27) ou
(2.28) -
b)
eles têm a mesma direção;
-
c)
eles são paralelos.
Demonstração.
De fato, a afirmação a) é a definição de dependência linear. A afirmação b) é consequência imediata da a), bem como a c) é equivalente a b). Por fim, se e são vetores paralelos, então um é múltiplo por escalar do outro. Ou seja, c) implica a). ∎
Esta proposição também mostra que dois vetores não nulos são linearmente independentes (l.i.) se, e somente se, eles têm direções diferentes.
Exemplo 2.2.2.
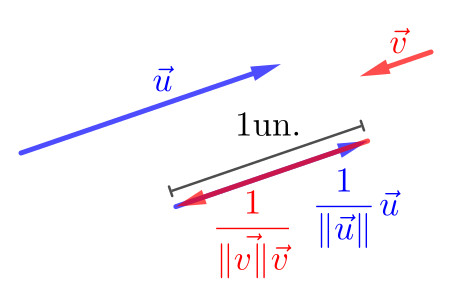
Considere dois vetores não nulos e de mesma direção. Então, no caso de terem sentidos opostos, segue que
| (2.29) |
noutro caso, temos que
| (2.30) |
Consulte a Figura 2.2.
2.2.2 Três Vetores no Espaço
Três vetores quaisquer , e são l.d., quando um deles pode ser escrito como combinação linear dos outros dois. Sem perda de generalidade, isto significa que existem constantes e tais que
| (2.31) |
ou, equivalentemente,
| (2.32) |
Afirmamos que se , e são l.d., então , e são coplanares. Do fato de que dois vetores quaisquer são sempre coplanares, temos que , e são coplanares caso qualquer um deles seja o vetor nulo. Suponhamos, agora, que , e são não nulos e seja o plano determinado pelos vetores e . Se , então e teríamos uma representação de no plano . Analogamente, se , então e teríamos uma representação de no plano . Por fim, observamos que se , então tem a mesma direção de e tem a mesma direção de . Isto é, e admitem representações no plano . Sejam e representações dos vetores e , respectivamente. Os pontos , e pertencem a , assim como o segmento . Como , concluímos que , e são coplanares.
Reciprocamente, se , e são coplanares, então , e são l.d.. Consulte a Figura 2.5.
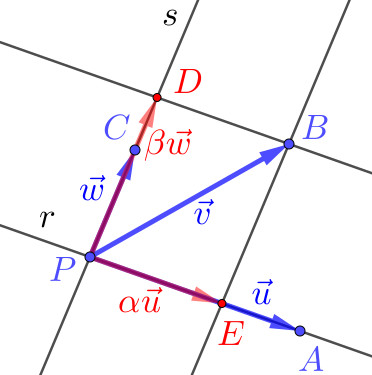
De fato, se um deles for nulo, por exemplo, , então pode ser escrito como a seguinte combinação linear dos vetores e
| (2.33) |
Neste caso, , e são l.d.. Também, se dois dos vetores forem paralelos, por exemplo, , então temos a combinação linear
| (2.34) |
E, então, , e são l.d.. Agora, suponhamos que , e são não nulos e dois a dois concorrentes (i.e. todos com direções distintas). Sejam, então , e representações sobre um plano . Sejam e as retas determinadas por e , respectivamente. Seja, então, o ponto de interseção da reta com a reta paralela a que passa pelo ponto . Seja, também, o ponto de interseção da reta com a reta paralela a que passa pelo ponto . Sejam, então, e tais que e . Como , temos que é combinação linear de e , i.e. , e são l.d..
2.2.3 Quatro ou Mais Vetores no Espaço
Quatro ou mais vetores são sempre l.d.77endnote: 7No espaço euclidiano tridimensional.. De fato, sejam dados quatro vetores , , e . Se dois ou três destes forem l.d.entre si, então, por definição, os quatro são l.d.. Assim sendo, suponhamos que três dos vetores sejam l.i. e provaremos que, então, o outro vetor é combinação linear desses três.
Sem perda de generalidade, suponhamos que , e são l.i.. Logo, eles não são coplanares. Seja, ainda, o plano determinado pelos vetores , e as representações , , e .
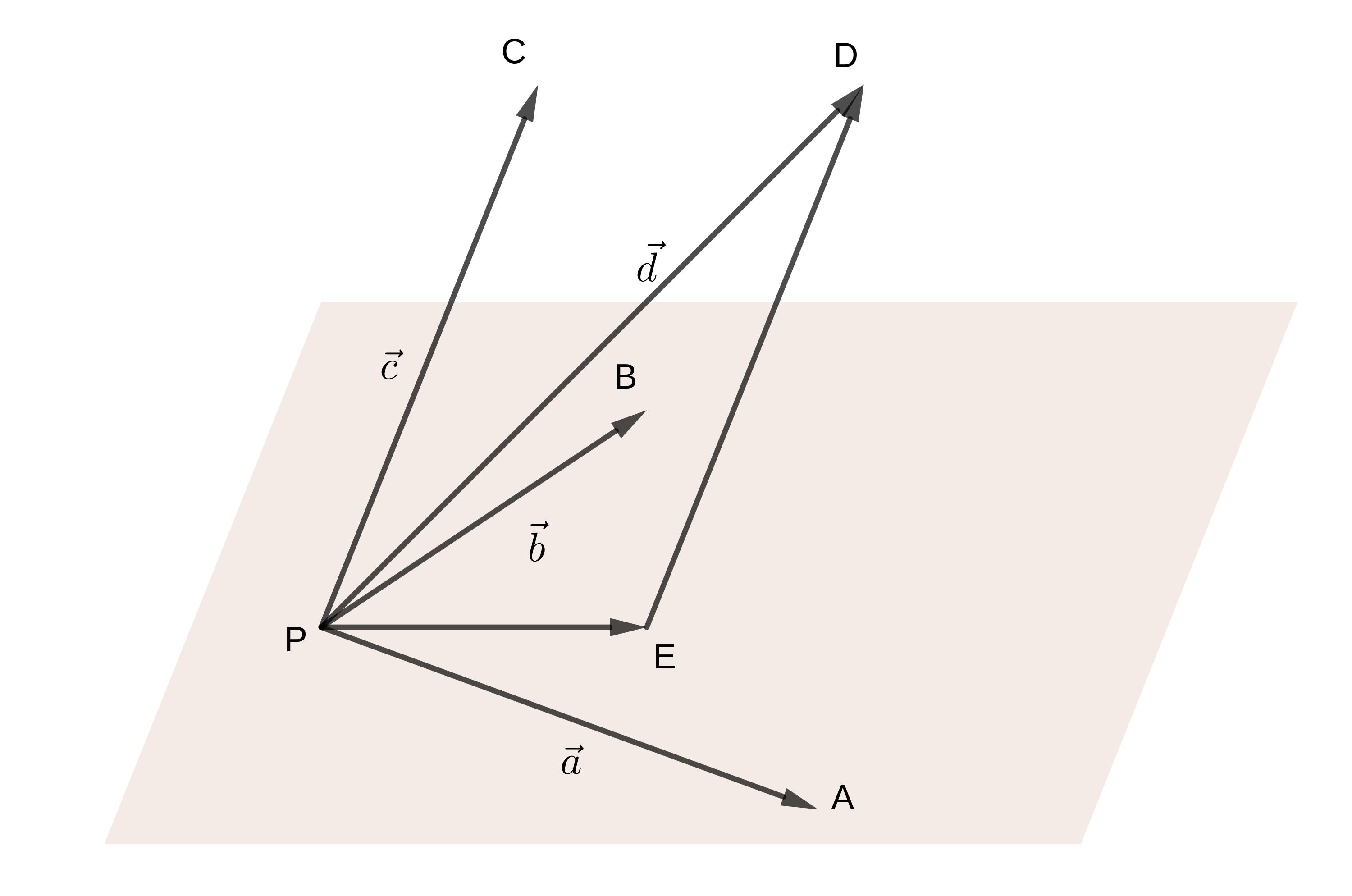
Tomamos a reta paralela a que passa pelo ponto . Então, seja o ponto de interseção de com o plano . Consultamos a Figura 2.6. Observamos que o vetor é coplanar aos vetores e e, portanto, exitem números reais e tal que
| (2.35) |
Além disso, como tem a mesma direção e sentido de , temos que
| (2.36) |
para algum número real . Por fim, observamos que
2.2.4 Exercícios Resolvidos
ER 2.2.1.
Se e são l.i. e
| (2.37) | ||||
| (2.38) |
então e são l.d.?
Solução 0.
Os vetores e são l.i. se, e somente se,
| (2.39) |
Observemos que
| (2.40) | ||||
| (2.41) | ||||
| (2.42) |
implica
| (2.43) | ||||
| (2.44) |
Resolvendo este sistema, vemos que . Logo, concluímos que e são l.i..
ER 2.2.2.
Sejam , e três vetores. Verifique a seguinte afirmação de que se e são l.d., então , e são l.d.. Justifique sua resposta.
Solução 0.
A afirmação é verdadeira. De fato, se e são l.d., então existe um escalar tal que
| (2.45) |
Segue que
| (2.46) |
Isto é, é combinação linear de e . Então, por definição, , e são l.d..
ER 2.2.3.
Sejam e . Mostre que , e são colineares se, e somente se, e são l.d..
Solução 0.
Primeiramente, vamos verificar a implicação. Se , e são colineares, então os segmentos e têm a mesma direção. Logo, são l.d. os vetores e .
Agora, verificamos a recíproca. Se e são l.d., então os segmentos e têm a mesma direção. Como eles são concorrentes, segue que , e são colineares.
2.2.5 Exercícios
E. 2.2.1.
Sendo , mostre que , e são l.d. para qualquer ponto .
Resposta 0.
Dica: os vetores e são l.d..
E. 2.2.2.
Sejam dados três vetores quaisquer , e . Mostre que os vetores , e são l.d..
Resposta 0.
Dica: Escreva um dos vetores como combinação linear dos outros.
E. 2.2.3.
Sejam , e . Mostre que , , e são coplanares se, e somente se, , e são l.d..
Resposta 0.
Três vetores são l.d. se, e somente se, eles são coplanares.
E. 2.2.4.
Se e são l.i. e
| (2.47) | |||
| (2.48) |
então e são l.i.? Justifique sua resposta.
Resposta 0.
Não.
E. 2.2.5.
Verifique se é verdadeira ou falsa cada uma das seguintes afirmações. Justifique sua resposta.
-
a)
, , l.d. , l.d..
-
b)
, , são l.d..
-
c)
, l.i. , e l.i..
-
d)
, , l.d. , , l.d..
Resposta 0.
a) falsa; b) verdadeira; c) falsa; d) verdadeira.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.2 Dependência Linear
Dois ou mais vetores dados são linearmente dependentes (l.d.) quando um deles for combinação linear dos demais. Mais precisamente, é um conjunto de vetores l.d. quando
| (2.23) |
para escalares não todos nulos. Caso contrário, dizemos tratar-se de um conjunto de vetores linearmente independentes (l.i.).
Exemplo 2.2.1.
Estudamos cada caso:
-
a)
Sejam e . Temos que e são linearmente dependentes, pois
(2.24) -
b)
Sejam , e . Temos que é um conjunto l.d., pois
(2.25)
Observação 2.2.1.
(Vetor Nulo.) Todo conjunto de vetores que contenha o vetor nulo é um conjunto l.d.. De fato, para quaisquer , , …, , tem-se que
| (2.26) |
2.2.1 Dois Vetores no Espaço
Dois vetores de mesma direção são linearmente dependentes (l.d.).
Proposição 2.2.1.
Dois vetores não nulos e são l.d. se, e somente se, qualquer uma das seguinte condições é satisfeita:
-
a)
um deles é combinação linear do outro, i.e.
(2.27) ou
(2.28) -
b)
eles têm a mesma direção;
-
c)
eles são paralelos.
Demonstração.
De fato, a afirmação a) é a definição de dependência linear. A afirmação b) é consequência imediata da a), bem como a c) é equivalente a b). Por fim, se e são vetores paralelos, então um é múltiplo por escalar do outro. Ou seja, c) implica a). ∎
Esta proposição também mostra que dois vetores não nulos são linearmente independentes (l.i.) se, e somente se, eles têm direções diferentes.
Exemplo 2.2.2.
Considere dois vetores não nulos e de mesma direção. Então, no caso de terem sentidos opostos, segue que
| (2.29) |
noutro caso, temos que
| (2.30) |
Consulte a Figura 2.2.

2.2.2 Três Vetores no Espaço
Três vetores quaisquer , e são l.d., quando um deles pode ser escrito como combinação linear dos outros dois. Sem perda de generalidade, isto significa que existem constantes e tais que
| (2.31) |
ou, equivalentemente,
| (2.32) |
Afirmamos que se , e são l.d., então , e são coplanares. Do fato de que dois vetores quaisquer são sempre coplanares, temos que , e são coplanares caso qualquer um deles seja o vetor nulo. Suponhamos, agora, que , e são não nulos e seja o plano determinado pelos vetores e . Se , então e teríamos uma representação de no plano . Analogamente, se , então e teríamos uma representação de no plano . Por fim, observamos que se , então tem a mesma direção de e tem a mesma direção de . Isto é, e admitem representações no plano . Sejam e representações dos vetores e , respectivamente. Os pontos , e pertencem a , assim como o segmento . Como , concluímos que , e são coplanares.
Reciprocamente, se , e são coplanares, então , e são l.d.. Consulte a Figura 2.5.

De fato, se um deles for nulo, por exemplo, , então pode ser escrito como a seguinte combinação linear dos vetores e
| (2.33) |
Neste caso, , e são l.d.. Também, se dois dos vetores forem paralelos, por exemplo, , então temos a combinação linear
| (2.34) |
E, então, , e são l.d.. Agora, suponhamos que , e são não nulos e dois a dois concorrentes (i.e. todos com direções distintas). Sejam, então , e representações sobre um plano . Sejam e as retas determinadas por e , respectivamente. Seja, então, o ponto de interseção da reta com a reta paralela a que passa pelo ponto . Seja, também, o ponto de interseção da reta com a reta paralela a que passa pelo ponto . Sejam, então, e tais que e . Como , temos que é combinação linear de e , i.e. , e são l.d..
2.2.3 Quatro ou Mais Vetores no Espaço
Quatro ou mais vetores são sempre l.d.77endnote: 7No espaço euclidiano tridimensional.. De fato, sejam dados quatro vetores , , e . Se dois ou três destes forem l.d.entre si, então, por definição, os quatro são l.d.. Assim sendo, suponhamos que três dos vetores sejam l.i. e provaremos que, então, o outro vetor é combinação linear desses três.
Sem perda de generalidade, suponhamos que , e são l.i.. Logo, eles não são coplanares. Seja, ainda, o plano determinado pelos vetores , e as representações , , e .

Tomamos a reta paralela a que passa pelo ponto . Então, seja o ponto de interseção de com o plano . Consultamos a Figura 2.6. Observamos que o vetor é coplanar aos vetores e e, portanto, exitem números reais e tal que
| (2.35) |
Além disso, como tem a mesma direção e sentido de , temos que
| (2.36) |
para algum número real . Por fim, observamos que
2.2.4 Exercícios Resolvidos
ER 2.2.1.
Se e são l.i. e
| (2.37) | ||||
| (2.38) |
então e são l.d.?
Solução 0.
Os vetores e são l.i. se, e somente se,
| (2.39) |
Observemos que
| (2.40) | ||||
| (2.41) | ||||
| (2.42) |
implica
| (2.43) | ||||
| (2.44) |
Resolvendo este sistema, vemos que . Logo, concluímos que e são l.i..
ER 2.2.2.
Sejam , e três vetores. Verifique a seguinte afirmação de que se e são l.d., então , e são l.d.. Justifique sua resposta.
Solução 0.
A afirmação é verdadeira. De fato, se e são l.d., então existe um escalar tal que
| (2.45) |
Segue que
| (2.46) |
Isto é, é combinação linear de e . Então, por definição, , e são l.d..
ER 2.2.3.
Sejam e . Mostre que , e são colineares se, e somente se, e são l.d..
Solução 0.
Primeiramente, vamos verificar a implicação. Se , e são colineares, então os segmentos e têm a mesma direção. Logo, são l.d. os vetores e .
Agora, verificamos a recíproca. Se e são l.d., então os segmentos e têm a mesma direção. Como eles são concorrentes, segue que , e são colineares.
2.2.5 Exercícios
E. 2.2.1.
Sendo , mostre que , e são l.d. para qualquer ponto .
Resposta 0.
Dica: os vetores e são l.d..
E. 2.2.2.
Sejam dados três vetores quaisquer , e . Mostre que os vetores , e são l.d..
Resposta 0.
Dica: Escreva um dos vetores como combinação linear dos outros.
E. 2.2.3.
Sejam , e . Mostre que , , e são coplanares se, e somente se, , e são l.d..
Resposta 0.
Três vetores são l.d. se, e somente se, eles são coplanares.
E. 2.2.4.
Se e são l.i. e
| (2.47) | |||
| (2.48) |
então e são l.i.? Justifique sua resposta.
Resposta 0.
Não.
E. 2.2.5.
Verifique se é verdadeira ou falsa cada uma das seguintes afirmações. Justifique sua resposta.
-
a)
, , l.d. , l.d..
-
b)
, , são l.d..
-
c)
, l.i. , e l.i..
-
d)
, , l.d. , , l.d..
Resposta 0.
a) falsa; b) verdadeira; c) falsa; d) verdadeira.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.