Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.2 Definição de Vetor
Um vetor é definido como a classe de equipolência22endnote: 2Consulte a Seção 1.1 para a definição de classe de equipolência. dos segmentos orientados de dado comprimento, dada direção e dado sentido, i.e. . Qualquer é uma representação do vetor como um segmento orientado. Consulte a Figura 1.9.
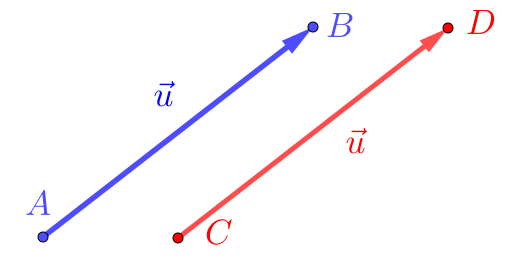
Observação 1.2.1.
(Notação.) Para simplificar a notação, usualmente, escrevemos no lugar de .
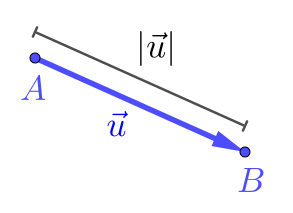
A norma de um vetor é denotada por e definida como o comprimento de qualquer uma de suas representações. Mais precisamente, se o segmento orientado é uma representação de , i.e. , então
| (1.7) |
Consulte a Figura 1.10.
O vetor nulo é aquele que tem como representante um segmento orientado nulo. É denotado por e geometricamente representado por um ponto.
Proposição 1.2.1.
(Vetor Nulo.) se, e somente se, .
Demonstração.
Primeiramente, vamos mostrar a implicação. Por hipótese, temos que . Seja, uma representação de . Então, por definição da norma de vetor, . Logo, é um segmento nulo, i.e. é coincidente a e, portanto, .
Agora, mostramos a recíproca, i.e., se , então . Como , temos que pode ser representado por qualquer segmento orientado . Temos que e, portanto, . ∎
Usualmente, escolhemos um ponto como origem do espaço. A seguinte proposição, garante que todo o vetor admite uma única representação a partir dessa origem.
Proposição 1.2.2.
(Representação de Vetor a partir da Origem) Seja dado um ponto no espaço. Todo vetor admite uma única representação .
Demonstração.
Seja dado um ponto e um vetor . Começamos por mostrar a existência, i.e. que existe tal que . Seja uma representação de e sua reta suporte. Seja, então, a reta que passa pelo ponto e é paralela (ou coincidente) a . Consulte a Figura 1.11.
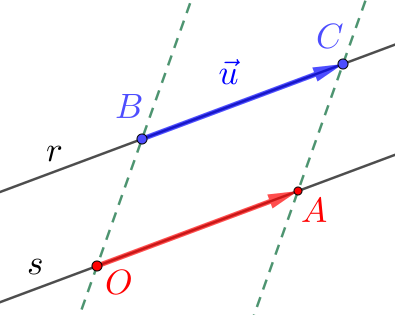
Escolhemos, então, tal que e tal que tenha o mesmo sentido de . Logo, é equipolente a , que é a representação desejada de .
Agora, vamos mostrar a unicidade, i.e. que se e são pontos tais que , então e são coincidentes. Por negação, se e não forem coincidentes, então , e são pontos colineares ou não, exclusivamente. Neste caso, e não tem a mesma direção. Noutro caso, ou e têm sentidos opostos. Em qualquer um dos casos . ∎
Dois vetores não nulos determinam um único ângulo33endnote: 3Mais precisamente, uma classe de ângulos congruentes.
Proposição 1.2.3.
(Ângulo entre Vetores.) Dois vetores não nulos determinam uma única classe de ângulos congruentes.
Demonstração.
Existência. Sejam dados os vetores e não nulos e suas representações e . Logo, e determinam duas semi-retas de ângulo (consulte a Figura 1.12).
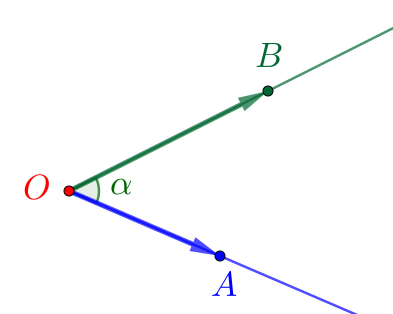
Unicidade. Sejam dois ângulos e determinados pelos vetores e . Sejam, também, as representações e . Logo, as semi-retas e têm as mesmas direções. Bem como, as semi-retas e têm as mesmas direções. Concluímos que os ângulos e são congruentes. ∎
Dois vetores são ditos paralelos quando admitem representações paralelas. De forma análoga, definem-se vetores coplanares, vetores não coplanares, vetores ortogonais, etc.
Exemplo 1.2.1.
Na Figura 1.13, temos vetor paralelo a , enquanto que é ortogonal a .
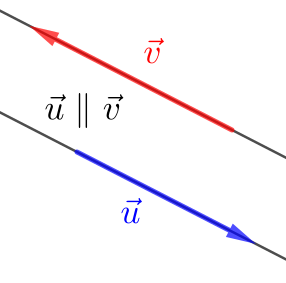
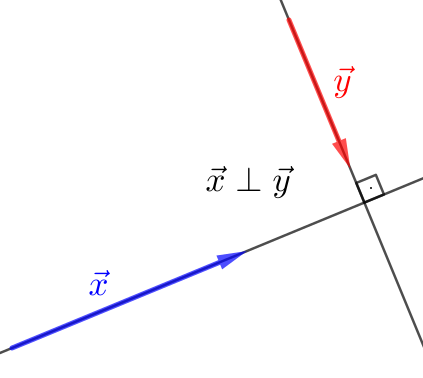
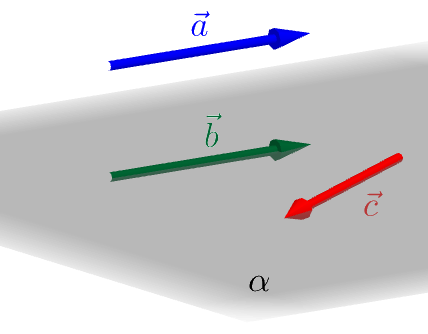
Agora, na Figura 1.14, temos que os vetores , e são coplanares.
1.2.1 Exercícios Resolvidos
ER 1.2.1.
Mostre que um plano fica unicamente determinado por um ponto e dois vetores não nulos de diferentes direções.
Solução 0.
Primeiramente, vamos mostrar a existência de um plano tal que (consulte a Figura 1.15). Sejam um ponto e dois vetores e não nulos e de diferentes direções. Escolhemos, então, suas representações e . Como e não nulos e têm diferentes direções, temos que os pontos , e são não colineares. Logo, estes pontos determinam um plano , tal que .
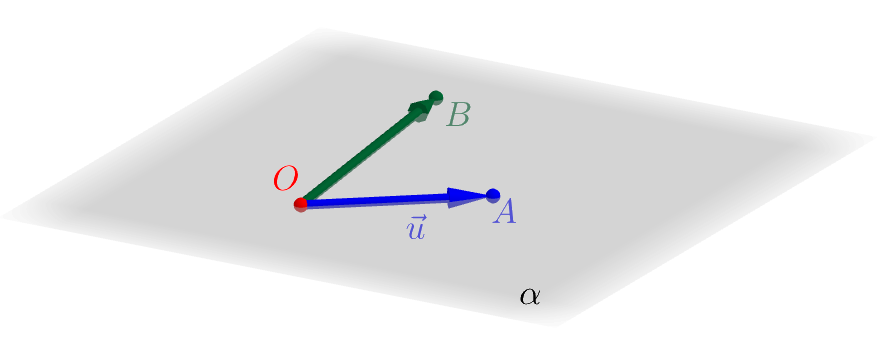
A unicidade segue imediatamente do fato de que três pontos não colineares determinam unicamente um plano.
ER 1.2.2.
Mostre que dois vetores não nulos e de diferentes direções determinam unicamente uma classe de paralelogramos congruentes44endnote: 4Dois polígonos são congruentes, quando seus lados e ângulos correspondentes têm a mesma medida..
Solução 0.
Existência. Sejam e dois vetores não nulos e de diferentes direções. Sejam, então, suas representações e (consulte a Figura 1.16). Sejam, agora, as retas e tais que , , e . Seja, o ponto de interseção de e . Por construção, temos que e , o que mostra que é um paralelogramo.
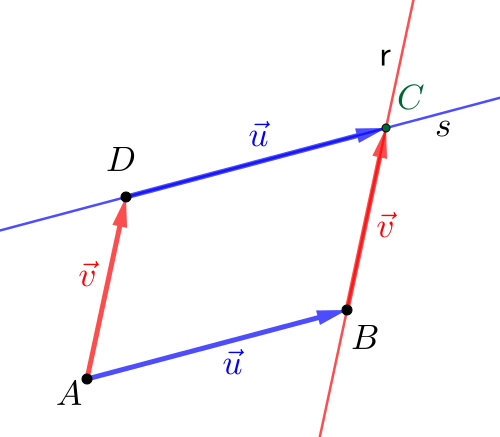
Unicidade. Falta mostrar que, dados e vetores não nulos e de diferentes direções, então são congruentes quaisquer dois paralelogramos determinados por e . Consulte o exercício E.1.2.9.
1.2.2 Exercícios
E. 1.2.1.
Complete as lacunas.
-
a)
Um vetor é definido por sua norma, direção e sentido.
-
b)
Se tem representação , então .
-
c)
Se , então é um vetor nulo.
-
d)
Vetores paralelos são vetores de mesma/o direção.
Resposta 0.
a) norma; sentido. b) . c) vetor nulo. d) direção.
E. 1.2.2.
Diga se é verdadeira ou falsa cada uma das seguintes afirmações:
-
a)
Todos os vetores podem ser representados a partir de um mesmo ponto de origem.
-
b)
Dois vetores de mesma norma são vetores paralelos.
-
c)
Dois vetores são sempre coplanares entre si.
Resposta 0.
a) V. b) F. c) V.
E. 1.2.3.
Diga se é verdadeira ou falsa cada uma das seguintes afirmações:
-
a)
Dois vetores não nulos determinam uma única classe de ângulos congruentes.
-
b)
Dois vetores não nulos de diferentes direções determinam um único plano.
-
c)
Dois vetores não nulos de diferentes direções determinam uma única classe de paralelogramos congruentes.
Resposta 0.
a) V. b) F. c) V.
E. 1.2.4.
Com base na figura abaixo, qual(is) dos vetores indicados são iguais ao vetor .
![[Uncaptioned image]](cap_vetor/dados/fig_exer_definicao_01/fig_exer_definicao_01.png)
Resposta 0.
E. 1.2.5.
Sejam , e pontos dois a dois distintos. Se é um vetor nulo, então é igual a:
-
a)
-
b)
-
c)
-
d)
-
e)
Resposta 0.
a), c), e)
E. 1.2.6.
Com base na figura abaixo, qual(is) dos vetores indicados são paralelos entre si.
![[Uncaptioned image]](cap_vetor/dados/fig_exer_definicao_01/fig_exer_definicao_01.png)
Resposta 0.
;
E. 1.2.7.
Com base na figura abaixo, qual(is) dos vetores indicados são ortogonais (perpendiculares) entre si.
![[Uncaptioned image]](cap_vetor/dados/fig_exer_definicao_01/fig_exer_definicao_01.png)
Resposta 0.
.
E. 1.2.8.
Mostre que uma reta fica unicamente determinada por um ponto e um vetor não nulo .
Resposta 0.
Seja tal que . Como , temos que e são não coincidentes. Temos então, uma única reta tal que .
E. 1.2.9.
No ER.1.2.2, mostrou-se que dados e vetores não nulos e de diferentes direções, então existe um paralelogramo associado de lados congruentes a e . Mostre que são congruentes quaisquer dois paralelogramos determinados por e .
Resposta 0.
Sejam as representações e . Do demonstrado no ER 1.2.2, temos os paralelogramos associados e . Por construção, é congruente a , bem como, são congruentes e . Também, são congruentes os ângulos e . Logo, conclui-se que os paralelogramos e são congruentes.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.2 Definição de Vetor
Um vetor é definido como a classe de equipolência22endnote: 2Consulte a Seção 1.1 para a definição de classe de equipolência. dos segmentos orientados de dado comprimento, dada direção e dado sentido, i.e. . Qualquer é uma representação do vetor como um segmento orientado. Consulte a Figura 1.9.

Observação 1.2.1.
(Notação.) Para simplificar a notação, usualmente, escrevemos no lugar de .
A norma de um vetor é denotada por e definida como o comprimento de qualquer uma de suas representações. Mais precisamente, se o segmento orientado é uma representação de , i.e. , então
| (1.7) |
Consulte a Figura 1.10.

O vetor nulo é aquele que tem como representante um segmento orientado nulo. É denotado por e geometricamente representado por um ponto.
Proposição 1.2.1.
(Vetor Nulo.) se, e somente se, .
Demonstração.
Primeiramente, vamos mostrar a implicação. Por hipótese, temos que . Seja, uma representação de . Então, por definição da norma de vetor, . Logo, é um segmento nulo, i.e. é coincidente a e, portanto, .
Agora, mostramos a recíproca, i.e., se , então . Como , temos que pode ser representado por qualquer segmento orientado . Temos que e, portanto, . ∎
Usualmente, escolhemos um ponto como origem do espaço. A seguinte proposição, garante que todo o vetor admite uma única representação a partir dessa origem.
Proposição 1.2.2.
(Representação de Vetor a partir da Origem) Seja dado um ponto no espaço. Todo vetor admite uma única representação .
Demonstração.
Seja dado um ponto e um vetor . Começamos por mostrar a existência, i.e. que existe tal que . Seja uma representação de e sua reta suporte. Seja, então, a reta que passa pelo ponto e é paralela (ou coincidente) a . Consulte a Figura 1.11.

Escolhemos, então, tal que e tal que tenha o mesmo sentido de . Logo, é equipolente a , que é a representação desejada de .
Agora, vamos mostrar a unicidade, i.e. que se e são pontos tais que , então e são coincidentes. Por negação, se e não forem coincidentes, então , e são pontos colineares ou não, exclusivamente. Neste caso, e não tem a mesma direção. Noutro caso, ou e têm sentidos opostos. Em qualquer um dos casos . ∎
Dois vetores não nulos determinam um único ângulo33endnote: 3Mais precisamente, uma classe de ângulos congruentes.
Proposição 1.2.3.
(Ângulo entre Vetores.) Dois vetores não nulos determinam uma única classe de ângulos congruentes.
Demonstração.
Existência. Sejam dados os vetores e não nulos e suas representações e . Logo, e determinam duas semi-retas de ângulo (consulte a Figura 1.12).

Unicidade. Sejam dois ângulos e determinados pelos vetores e . Sejam, também, as representações e . Logo, as semi-retas e têm as mesmas direções. Bem como, as semi-retas e têm as mesmas direções. Concluímos que os ângulos e são congruentes. ∎
Dois vetores são ditos paralelos quando admitem representações paralelas. De forma análoga, definem-se vetores coplanares, vetores não coplanares, vetores ortogonais, etc.
Exemplo 1.2.1.
Na Figura 1.13, temos vetor paralelo a , enquanto que é ortogonal a .


Agora, na Figura 1.14, temos que os vetores , e são coplanares.

1.2.1 Exercícios Resolvidos
ER 1.2.1.
Mostre que um plano fica unicamente determinado por um ponto e dois vetores não nulos de diferentes direções.
Solução 0.
Primeiramente, vamos mostrar a existência de um plano tal que (consulte a Figura 1.15). Sejam um ponto e dois vetores e não nulos e de diferentes direções. Escolhemos, então, suas representações e . Como e não nulos e têm diferentes direções, temos que os pontos , e são não colineares. Logo, estes pontos determinam um plano , tal que .

A unicidade segue imediatamente do fato de que três pontos não colineares determinam unicamente um plano.
ER 1.2.2.
Mostre que dois vetores não nulos e de diferentes direções determinam unicamente uma classe de paralelogramos congruentes44endnote: 4Dois polígonos são congruentes, quando seus lados e ângulos correspondentes têm a mesma medida..
Solução 0.
Existência. Sejam e dois vetores não nulos e de diferentes direções. Sejam, então, suas representações e (consulte a Figura 1.16). Sejam, agora, as retas e tais que , , e . Seja, o ponto de interseção de e . Por construção, temos que e , o que mostra que é um paralelogramo.

Unicidade. Falta mostrar que, dados e vetores não nulos e de diferentes direções, então são congruentes quaisquer dois paralelogramos determinados por e . Consulte o exercício E.1.2.9.
1.2.2 Exercícios
E. 1.2.1.
Complete as lacunas.
-
a)
Um vetor é definido por sua norma, direção e sentido.
-
b)
Se tem representação , então .
-
c)
Se , então é um vetor nulo.
-
d)
Vetores paralelos são vetores de mesma/o direção.
Resposta 0.
a) norma; sentido. b) . c) vetor nulo. d) direção.
E. 1.2.2.
Diga se é verdadeira ou falsa cada uma das seguintes afirmações:
-
a)
Todos os vetores podem ser representados a partir de um mesmo ponto de origem.
-
b)
Dois vetores de mesma norma são vetores paralelos.
-
c)
Dois vetores são sempre coplanares entre si.
Resposta 0.
a) V. b) F. c) V.
E. 1.2.3.
Diga se é verdadeira ou falsa cada uma das seguintes afirmações:
-
a)
Dois vetores não nulos determinam uma única classe de ângulos congruentes.
-
b)
Dois vetores não nulos de diferentes direções determinam um único plano.
-
c)
Dois vetores não nulos de diferentes direções determinam uma única classe de paralelogramos congruentes.
Resposta 0.
a) V. b) F. c) V.
E. 1.2.4.
Com base na figura abaixo, qual(is) dos vetores indicados são iguais ao vetor .
![[Uncaptioned image]](cap_vetor/dados/fig_exer_definicao_01/fig_exer_definicao_01.png)
Resposta 0.
E. 1.2.5.
Sejam , e pontos dois a dois distintos. Se é um vetor nulo, então é igual a:
-
a)
-
b)
-
c)
-
d)
-
e)
Resposta 0.
a), c), e)
E. 1.2.6.
Com base na figura abaixo, qual(is) dos vetores indicados são paralelos entre si.
![[Uncaptioned image]](cap_vetor/dados/fig_exer_definicao_01/fig_exer_definicao_01.png)
Resposta 0.
;
E. 1.2.7.
Com base na figura abaixo, qual(is) dos vetores indicados são ortogonais (perpendiculares) entre si.
![[Uncaptioned image]](cap_vetor/dados/fig_exer_definicao_01/fig_exer_definicao_01.png)
Resposta 0.
.
E. 1.2.8.
Mostre que uma reta fica unicamente determinada por um ponto e um vetor não nulo .
Resposta 0.
Seja tal que . Como , temos que e são não coincidentes. Temos então, uma única reta tal que .
E. 1.2.9.
No ER.1.2.2, mostrou-se que dados e vetores não nulos e de diferentes direções, então existe um paralelogramo associado de lados congruentes a e . Mostre que são congruentes quaisquer dois paralelogramos determinados por e .
Resposta 0.
Sejam as representações e . Do demonstrado no ER 1.2.2, temos os paralelogramos associados e . Por construção, é congruente a , bem como, são congruentes e . Também, são congruentes os ângulos e . Logo, conclui-se que os paralelogramos e são congruentes.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.