Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Matemática Numérica II
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
6.1 Equação de Poisson
Consideramos a equação de Poisson2828endnote: 28Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson. (ou equação de Laplace2929endnote: 29Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace. heterogênea) no domínio retangular com condições de contorno de Dirichlet homogêneas
| (6.1a) | |||
| (6.1b) | |||
onde é a incógnita, e é a fronteira do domínio .
A aplicação do Método de Diferenças Finitas para resolver este problema consiste dos mesmos passos usados para resolver problemas de valores de contorno (consulte Seção 5.1), a saber: 1. discretização do domínio, 2. discretização das equações, 3. resolução do problema discreto.
1. Discretização do Domínio (Malha).
Tratando-se do domínio retangular , podemos construir uma malha do produto cartesiano de partições uniformes dos intervalos e . Ou seja, tomamos
| (6.2a) | ||||
| (6.2b) | ||||
com , , sendo e o número de subintervalos escolhidos para as partições, respectivamente, e os passos e . O tamanho da malha é definido por .
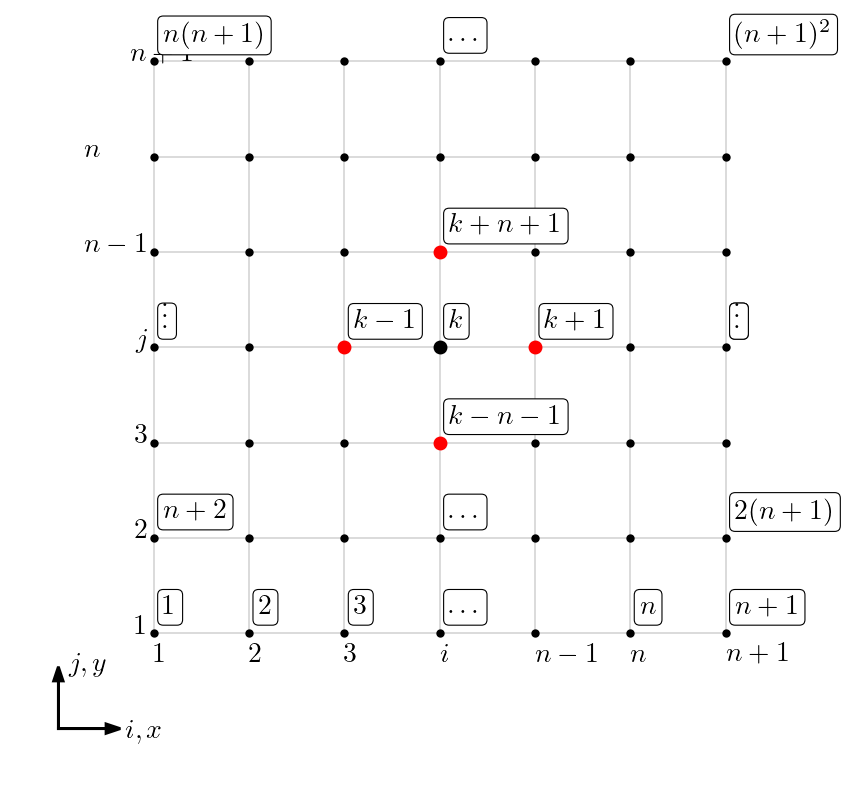
O produto cartesiano das partições em e nos fornece uma partição do domínio da forma
| (6.3) |
cujos nodos podem ser enumerados (indexados) por . Por simplicidade, no decorrer do texto, assumiremos e, por conseguinte, e temos a enumeração
| (6.4) |
Consulte a Figura 6.1.
2. Discretização das Equações.
Usando a fórmula de diferenças finitas central de ordem para a segunda derivada, temos
| (6.5) | ||||
| (6.6) |
Daí, denotando temos
| (6.7) | ||||
| (6.8) |
Então, da Eq. 6.1a temos
| (6.9) | ||||
Agora, com base na enumeração (6.4) denotamos , desprezando o erro de truncamento e rearranjando os termos, obtemos
| (6.10) |
para com (nodos internos). Isto é, esta última expressão nos fornece um sistema de equações para incógnitas . Para fechar o sistema, usamos as condições de contorno (6.1b)
| (6.11) |
para com e , ou e .
Com isso, o problema discreto obtido da aplicação do MDF consiste no sistema linear de (6.10)-(6.11).
3. Resolução do Problema Discreto.
O problema discreto (6.10)-(6.11) pode ser escrito na forma matricial
| (6.12) |
onde o vetor da incógnitas é . A matriz dos coeficientes e o vetor dos termos contantes têm elementos não nulos
| (6.13) | ||||
| (6.14) | ||||
| (6.15) | |||||
Assim sendo, basta empregarmos um método apropriado para resolver o sistema linear (6.12) para obter a solução aproximada de nos nodos .
Exemplo 6.1.1.
Consideramos o seguinte problema
| (6.16a) | |||
| (6.16b) | |||
A solução exata é .
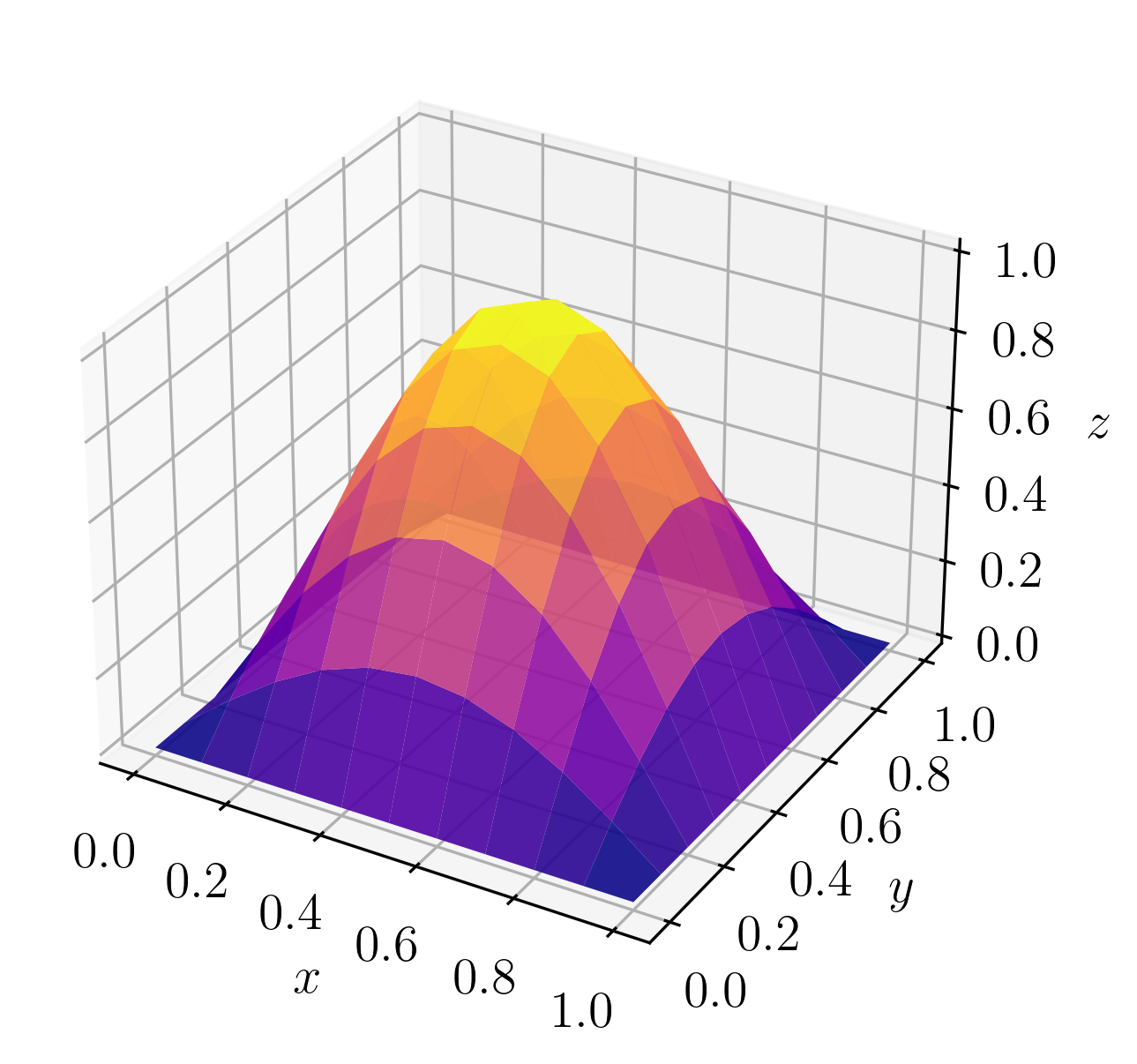
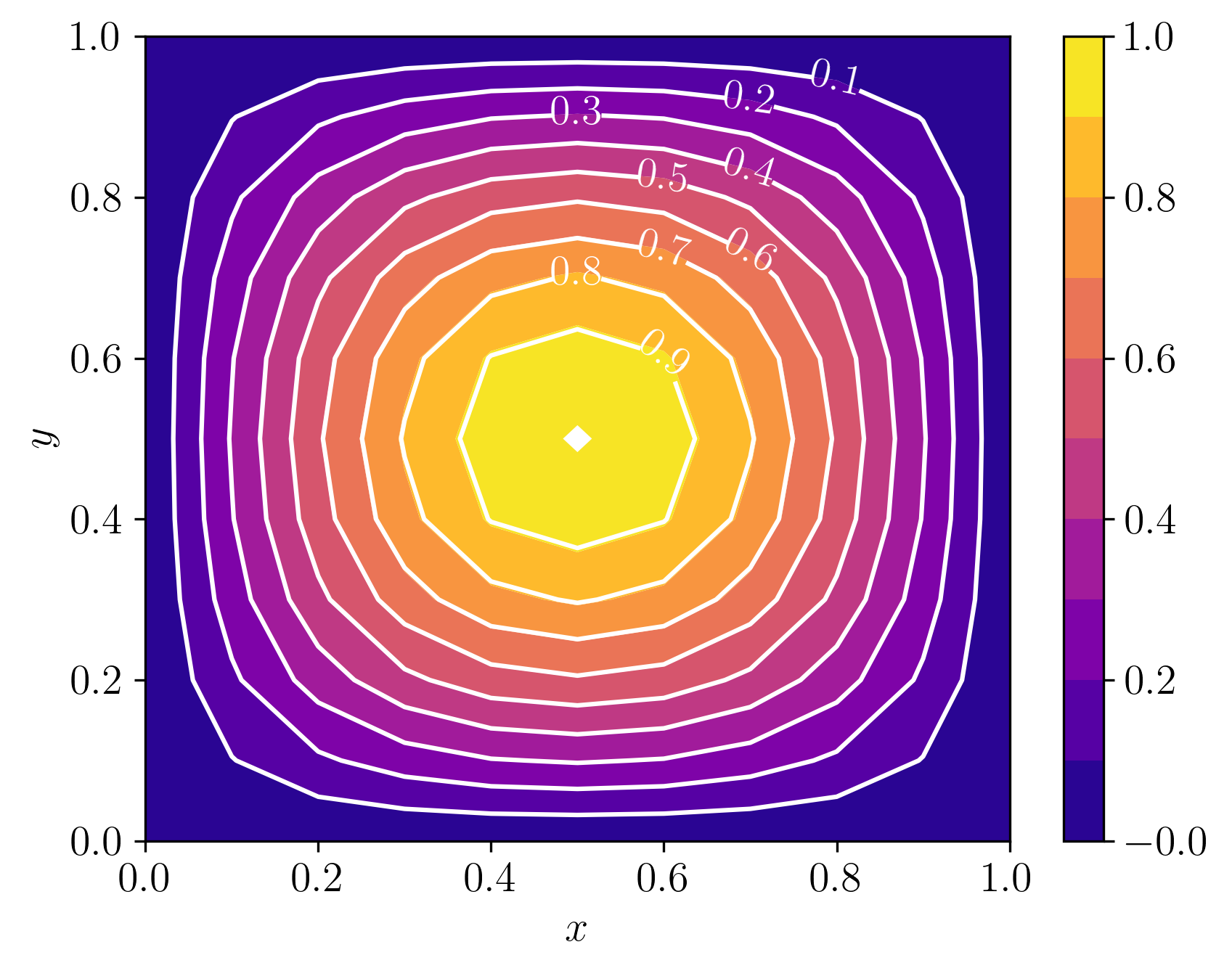
A Figura 6.2 mostra o gráfico de superfície da solução aproximada obtida pelo MDF com . A Figura 6.3 mostra a comparação entre os gráficos de contorno das soluções numérica e exata (linhas brancas).
6.1.1 Exercícios
E. 6.1.1.
Use o MDF para encontrar uma solução aproximada do seguinte problema de Poisson
| (6.17a) | |||
| (6.17b) | |||
A solução exata é . Faça uma comparação gráfica entre as soluções numérica e exata no caso de (malha uniforme). Compare o erro para (número de subintervalos na malha uniforme). A taxa de convergência é a esperada? Justifique sua resposta.
E. 6.1.2.
Use o MDF para encontrar uma solução aproximada do seguinte problema de Laplace
| (6.18a) | |||
| (6.18b) | |||
| (6.18c) | |||
A solução exata é . Faça uma comparação gráfica entre as soluções numérica e exata no caso de . Compare o erro para (número de subintervalos na malha uniforme).
E. 6.1.3.
Considere o problema
| (6.19a) | |||
| (6.19b) | |||
| (6.19c) | |||
| (6.19d) | |||
A solução exata é . Com uma malha uniforme, obtenha uma solução aproximada com o MDF empregando, na fronteira com condições de Neumann3030endnote: 30Carl Gottfried Neumann, 1832 - 1925, matemático alemão. Fonte: Wikipédia: Carl Neumann.:
-
a)
fórmulas diferença regressiva de ordem .
-
b)
diferença regressiva de ordem .
Compare a taxa de convergência do erro entre essas duas formulações.
E. 6.1.4.
Considere o problema
| (6.20a) | |||
| (6.20b) | |||
| (6.20c) | |||
A solução exata é . Com uma malha uniforme, obtenha uma solução aproximada com o MDF empregando, nas fronteiras com condições de Neumann:
-
a)
fórmulas de diferenças finitas de .
-
b)
fórmulas de diferenças finitas de .
Compare a taxa de convergência do erro entre essas duas formulações.
E. 6.1.5.
Use o MDF para encontrar uma solução aproximada do seguinte problema de Poisson
| (6.21a) | |||
| (6.21b) | |||
Usando uma malha uniforme, obtenha soluções para (número de subintervalos). Sua solução está correta? Justifique sua resposta.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Matemática Numérica II
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
6.1 Equação de Poisson
Consideramos a equação de Poisson2828endnote: 28Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson. (ou equação de Laplace2929endnote: 29Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace. heterogênea) no domínio retangular com condições de contorno de Dirichlet homogêneas
| (6.1a) | |||
| (6.1b) | |||
onde é a incógnita, e é a fronteira do domínio .
A aplicação do Método de Diferenças Finitas para resolver este problema consiste dos mesmos passos usados para resolver problemas de valores de contorno (consulte Seção 5.1), a saber: 1. discretização do domínio, 2. discretização das equações, 3. resolução do problema discreto.
1. Discretização do Domínio (Malha).
Tratando-se do domínio retangular , podemos construir uma malha do produto cartesiano de partições uniformes dos intervalos e . Ou seja, tomamos
| (6.2a) | ||||
| (6.2b) | ||||
com , , sendo e o número de subintervalos escolhidos para as partições, respectivamente, e os passos e . O tamanho da malha é definido por .

O produto cartesiano das partições em e nos fornece uma partição do domínio da forma
| (6.3) |
cujos nodos podem ser enumerados (indexados) por . Por simplicidade, no decorrer do texto, assumiremos e, por conseguinte, e temos a enumeração
| (6.4) |
Consulte a Figura 6.1.
2. Discretização das Equações.
Usando a fórmula de diferenças finitas central de ordem para a segunda derivada, temos
| (6.5) | ||||
| (6.6) |
Daí, denotando temos
| (6.7) | ||||
| (6.8) |
Então, da Eq. 6.1a temos
| (6.9) | ||||
Agora, com base na enumeração (6.4) denotamos , desprezando o erro de truncamento e rearranjando os termos, obtemos
| (6.10) |
para com (nodos internos). Isto é, esta última expressão nos fornece um sistema de equações para incógnitas . Para fechar o sistema, usamos as condições de contorno (6.1b)
| (6.11) |
para com e , ou e .
Com isso, o problema discreto obtido da aplicação do MDF consiste no sistema linear de (6.10)-(6.11).
3. Resolução do Problema Discreto.
O problema discreto (6.10)-(6.11) pode ser escrito na forma matricial
| (6.12) |
onde o vetor da incógnitas é . A matriz dos coeficientes e o vetor dos termos contantes têm elementos não nulos
| (6.13) | ||||
| (6.14) | ||||
| (6.15) | |||||
Assim sendo, basta empregarmos um método apropriado para resolver o sistema linear (6.12) para obter a solução aproximada de nos nodos .
Exemplo 6.1.1.
Consideramos o seguinte problema
| (6.16a) | |||
| (6.16b) | |||
A solução exata é .
A Figura 6.2 mostra o gráfico de superfície da solução aproximada obtida pelo MDF com . A Figura 6.3 mostra a comparação entre os gráficos de contorno das soluções numérica e exata (linhas brancas).


6.1.1 Exercícios
E. 6.1.1.
Use o MDF para encontrar uma solução aproximada do seguinte problema de Poisson
| (6.17a) | |||
| (6.17b) | |||
A solução exata é . Faça uma comparação gráfica entre as soluções numérica e exata no caso de (malha uniforme). Compare o erro para (número de subintervalos na malha uniforme). A taxa de convergência é a esperada? Justifique sua resposta.
E. 6.1.2.
Use o MDF para encontrar uma solução aproximada do seguinte problema de Laplace
| (6.18a) | |||
| (6.18b) | |||
| (6.18c) | |||
A solução exata é . Faça uma comparação gráfica entre as soluções numérica e exata no caso de . Compare o erro para (número de subintervalos na malha uniforme).
E. 6.1.3.
Considere o problema
| (6.19a) | |||
| (6.19b) | |||
| (6.19c) | |||
| (6.19d) | |||
A solução exata é . Com uma malha uniforme, obtenha uma solução aproximada com o MDF empregando, na fronteira com condições de Neumann3030endnote: 30Carl Gottfried Neumann, 1832 - 1925, matemático alemão. Fonte: Wikipédia: Carl Neumann.:
-
a)
fórmulas diferença regressiva de ordem .
-
b)
diferença regressiva de ordem .
Compare a taxa de convergência do erro entre essas duas formulações.
E. 6.1.4.
Considere o problema
| (6.20a) | |||
| (6.20b) | |||
| (6.20c) | |||
A solução exata é . Com uma malha uniforme, obtenha uma solução aproximada com o MDF empregando, nas fronteiras com condições de Neumann:
-
a)
fórmulas de diferenças finitas de .
-
b)
fórmulas de diferenças finitas de .
Compare a taxa de convergência do erro entre essas duas formulações.
E. 6.1.5.
Use o MDF para encontrar uma solução aproximada do seguinte problema de Poisson
| (6.21a) | |||
| (6.21b) | |||
Usando uma malha uniforme, obtenha soluções para (número de subintervalos). Sua solução está correta? Justifique sua resposta.
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.