Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Matemática Numérica II
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
6.2 Equação do Calor
Consideramos a equação do calor com condição inicial dada e condições de contorno de Dirichlet homogêneas
| (6.22a) | |||
| (6.22b) | |||
| (6.22c) | |||
onde é a incógnita.
O problema (6.22) é um problema de valor inicial com condições de contorno. Uma das estratégias numéricas de solução é o chamado Método das Linhas, o qual trata separadamente as discretizações espacial e temporal. Aqui, vamos começar pela discretização espacial e, então, trataremos a discretização temporal.
1. Discretização Espacial.
Na discretização espacial, aplicamos o Método de Diferenças Finitas (MDF). Começamos considerando uma malha uniforme de nodos , , com tamanho de malha , sendo o número de subintervalos. Denotando e empregando a fórmula de diferenças finitas centrais , temos que a Eq. (6.22a) fica aproximada por
| (6.23) |
para . Agora, das condições de contorno (6.22c), temos e . Com isso, obtemos o seguinte sistema de equações diferenciais ordinárias
| (6.24a) | |||
| (6.24b) | |||
| (6.24c) | |||
onde e com condições iniciais dadas por (6.22b), i.e.
| (6.25) |
para . Este sistema pode ser escrito na seguinte forma matricial
| (6.26) |
onde , e é uma matriz da forma
| (6.27) |
2. Discretização Temporal.
Para a discretização temporal vamos usar o esquema-. Consideramos os tempos discretos , com passo no tempo , para . Denotando , o esquema consiste nas iterações
| (6.28a) | |||
| (6.28b) | |||
para e para um escolhido . No caso, não depende de e a Eq. (6.28b) é equivalente ao sistema linear
| (6.29) |
com .
Observação 6.2.1.
(Estabilidade e Erro de Truncamento.) Para (Método de Euler Explícito) o esquema numérico condicionalmente estável [2, Cap. 12, Seç. 2] para
| (6.30) |
Para (Método de Euler Implícito) o esquema é incondicionalmente estável. Em ambos estes casos, o erro de truncamento é . Escolhendo-se (Método de Crank-Nicolson), o esquema numérico é incondicionalmente estável e com erro de truncamento .
Exemplo 6.2.1.
Consideramos o seguinte problema de calor
| (6.31a) | |||
| (6.31b) | |||
| (6.31c) | |||
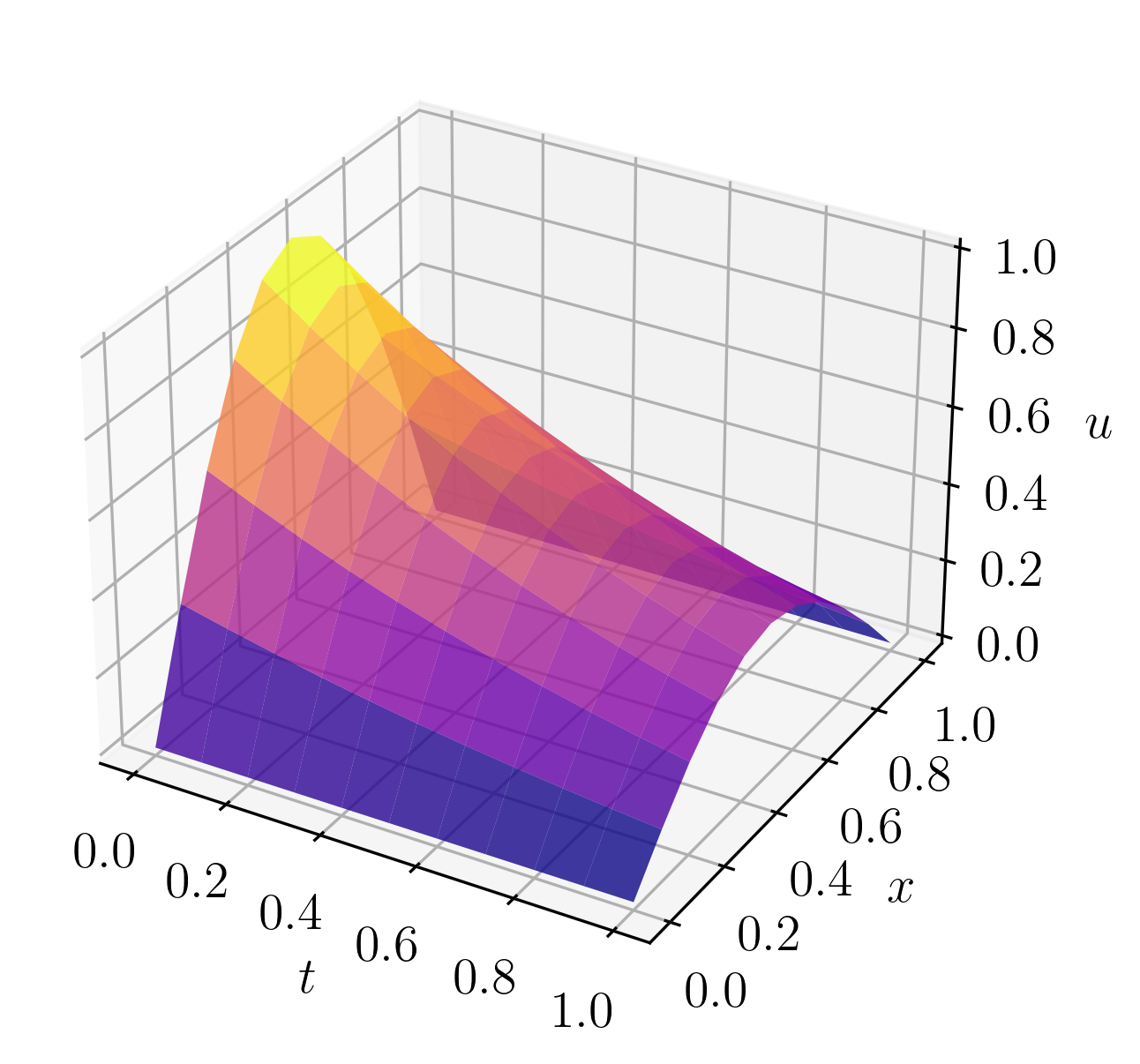
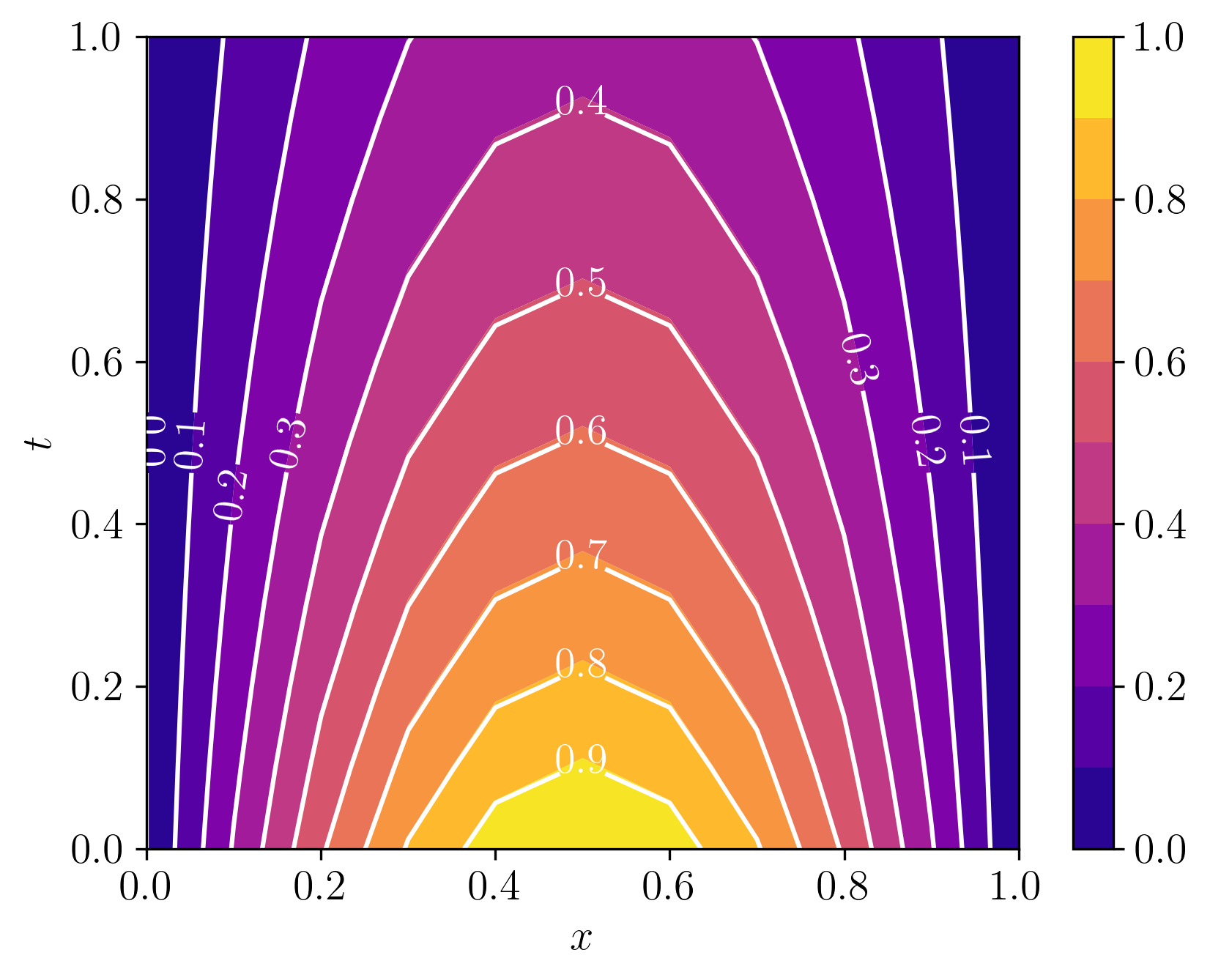
Este problema tem solução exata . A Figura 6.4 mostra o gráfico de superfície da solução numérica. Na Figura 6.5, temos a comparação entre a solução numérica e a solução exata (isolinhas).
6.2.1 Exercícios
E. 6.2.1.
Considere o problema
| (6.32a) | |||
| (6.32b) | |||
| (6.32c) | |||
Sua solução exata é . Implemente o MDF com esquema- em uma malha uniforme de tamanho espacial e passo no tempo para obter uma solução numérica . Então, verifique a taxa de convergência do erro para os diferentes esquemas:
-
a)
Euler Explícito: .
-
b)
Euler Implícito: .
-
c)
Crank-Nicolson: .
E. 6.2.2.
Considere o problema
| (6.33a) | |||
| (6.33b) | |||
| (6.33c) | |||
Sua solução exata é . Implemente o MDF com esquema- em uma malha uniforme. Faça testes numéricos para analisar a validade da condição de estabilidade (6.30) para os seguintes esquemas:
-
a)
Euler Explícito: .
-
b)
Euler Implícito: .
-
c)
Crank-Nicolson: .
E. 6.2.3.
Considere o problema
| (6.34a) | |||
| (6.34b) | |||
| (6.34c) | |||
| (6.34d) | |||
Sua solução exata é . Implemente o MDF com esquema- em uma malha uniforme de tamanho espacial e passo no tempo para obter uma solução numérica . Então, verifique a taxa de convergência do erro para os diferentes esquemas:
-
a)
Euler Explícito: .
-
b)
Euler Implícito: .
-
c)
Crank-Nicolson: .
E. 6.2.4.
Considere o problema
| (6.35a) | |||
| (6.35b) | |||
| (6.35c) | |||
| (6.35d) | |||
Sua solução exata é . Implemente o MDF com o Método de Crank-Nicolson em uma malha uniforme para obter uma solução numérica . Então, verifique a taxa de convergência do erro para os seguintes diferentes esquemas:
-
a)
empregando a diferença finita na condição de contorno de Neumann.
-
b)
empregando a diferença finita na condição de contorno de Neumann.
E. 6.2.5.
Considere o seguinte problema de calor
| (6.36a) | |||
| (6.36b) | |||
| (6.36c) | |||
Sua solução exata . Faça implementações numéricas do Método das Linhas com MDF na discretização espacial e empregando os seguintes métodos de Runge-Kutta para resolver o sistema de EDOs associado:
-
a)
Método do Ponto Médio.
-
b)
Método de R-K-4.
E. 6.2.6.
(Equação de Burgers.) Considere o problema
| (6.37a) | |||
| (6.37b) | |||
| (6.37c) | |||
Sua solução analítica é [9]
| (6.38) |
Faça uma implementação numérica com MDF e com esquema- para resolver este problema. Teste os esquemas para .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Matemática Numérica II
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
6.2 Equação do Calor
Consideramos a equação do calor com condição inicial dada e condições de contorno de Dirichlet homogêneas
| (6.22a) | |||
| (6.22b) | |||
| (6.22c) | |||
onde é a incógnita.
O problema (6.22) é um problema de valor inicial com condições de contorno. Uma das estratégias numéricas de solução é o chamado Método das Linhas, o qual trata separadamente as discretizações espacial e temporal. Aqui, vamos começar pela discretização espacial e, então, trataremos a discretização temporal.
1. Discretização Espacial.
Na discretização espacial, aplicamos o Método de Diferenças Finitas (MDF). Começamos considerando uma malha uniforme de nodos , , com tamanho de malha , sendo o número de subintervalos. Denotando e empregando a fórmula de diferenças finitas centrais , temos que a Eq. (6.22a) fica aproximada por
| (6.23) |
para . Agora, das condições de contorno (6.22c), temos e . Com isso, obtemos o seguinte sistema de equações diferenciais ordinárias
| (6.24a) | |||
| (6.24b) | |||
| (6.24c) | |||
onde e com condições iniciais dadas por (6.22b), i.e.
| (6.25) |
para . Este sistema pode ser escrito na seguinte forma matricial
| (6.26) |
onde , e é uma matriz da forma
| (6.27) |
2. Discretização Temporal.
Para a discretização temporal vamos usar o esquema-. Consideramos os tempos discretos , com passo no tempo , para . Denotando , o esquema consiste nas iterações
| (6.28a) | |||
| (6.28b) | |||
para e para um escolhido . No caso, não depende de e a Eq. (6.28b) é equivalente ao sistema linear
| (6.29) |
com .
Observação 6.2.1.
(Estabilidade e Erro de Truncamento.) Para (Método de Euler Explícito) o esquema numérico condicionalmente estável [2, Cap. 12, Seç. 2] para
| (6.30) |
Para (Método de Euler Implícito) o esquema é incondicionalmente estável. Em ambos estes casos, o erro de truncamento é . Escolhendo-se (Método de Crank-Nicolson), o esquema numérico é incondicionalmente estável e com erro de truncamento .
Exemplo 6.2.1.
Consideramos o seguinte problema de calor
| (6.31a) | |||
| (6.31b) | |||
| (6.31c) | |||
Este problema tem solução exata . A Figura 6.4 mostra o gráfico de superfície da solução numérica. Na Figura 6.5, temos a comparação entre a solução numérica e a solução exata (isolinhas).


6.2.1 Exercícios
E. 6.2.1.
Considere o problema
| (6.32a) | |||
| (6.32b) | |||
| (6.32c) | |||
Sua solução exata é . Implemente o MDF com esquema- em uma malha uniforme de tamanho espacial e passo no tempo para obter uma solução numérica . Então, verifique a taxa de convergência do erro para os diferentes esquemas:
-
a)
Euler Explícito: .
-
b)
Euler Implícito: .
-
c)
Crank-Nicolson: .
E. 6.2.2.
Considere o problema
| (6.33a) | |||
| (6.33b) | |||
| (6.33c) | |||
Sua solução exata é . Implemente o MDF com esquema- em uma malha uniforme. Faça testes numéricos para analisar a validade da condição de estabilidade (6.30) para os seguintes esquemas:
-
a)
Euler Explícito: .
-
b)
Euler Implícito: .
-
c)
Crank-Nicolson: .
E. 6.2.3.
Considere o problema
| (6.34a) | |||
| (6.34b) | |||
| (6.34c) | |||
| (6.34d) | |||
Sua solução exata é . Implemente o MDF com esquema- em uma malha uniforme de tamanho espacial e passo no tempo para obter uma solução numérica . Então, verifique a taxa de convergência do erro para os diferentes esquemas:
-
a)
Euler Explícito: .
-
b)
Euler Implícito: .
-
c)
Crank-Nicolson: .
E. 6.2.4.
Considere o problema
| (6.35a) | |||
| (6.35b) | |||
| (6.35c) | |||
| (6.35d) | |||
Sua solução exata é . Implemente o MDF com o Método de Crank-Nicolson em uma malha uniforme para obter uma solução numérica . Então, verifique a taxa de convergência do erro para os seguintes diferentes esquemas:
-
a)
empregando a diferença finita na condição de contorno de Neumann.
-
b)
empregando a diferença finita na condição de contorno de Neumann.
E. 6.2.5.
Considere o seguinte problema de calor
| (6.36a) | |||
| (6.36b) | |||
| (6.36c) | |||
Sua solução exata . Faça implementações numéricas do Método das Linhas com MDF na discretização espacial e empregando os seguintes métodos de Runge-Kutta para resolver o sistema de EDOs associado:
-
a)
Método do Ponto Médio.
-
b)
Método de R-K-4.
E. 6.2.6.
(Equação de Burgers.) Considere o problema
| (6.37a) | |||
| (6.37b) | |||
| (6.37c) | |||
Sua solução analítica é [9]
| (6.38) |
Faça uma implementação numérica com MDF e com esquema- para resolver este problema. Teste os esquemas para .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.