Vetores

2 Bases e coordenadas 2.2 Dependência linear 2.4 Mudança de base

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.3 Bases e coordenadas

Seja $V$ o conjunto de todos os vetores no espaço tridimensional. Conforme discutido na Seção 2.2, se $\vec{a}$ , $\vec{b}$ e $\vec{c}$ são l.i., então qualquer vetor $\vec{u}\in V$ pode ser escrito como uma combinação linear destes vetores, i.e. existem escalares $\alpha$ , $\beta$ e $\gamma$ tal que

\vec{u}=\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}.

(2.49)

Isso motiva a seguinte definição: uma base de $V$ é uma sequência de três vetores l.i. de $V$ .

A seguinte proposição vai nos fornecer a noção de coordenadas no espaço.

Proposição 2.3.1.

Seja $B=\left(\vec{a},\vec{b},\vec{c}\right)$ uma base de $V$ . Então, dado qualquer $\vec{u}\in V$ , existe uma única tripla de escalares $\left(\alpha,\beta,\gamma\right)$ tais que

\vec{u}=\alpha\vec{a}+\beta\vec{b}+\gamma\vec{c}.

(2.50)

Demonstração.

A existência dos escalares $\alpha$ , $\beta$ e $\gamma$ segue imediatamente do fato de que $\vec{a}$ , $\vec{b}$ e $\vec{c}$ são l.i. e, portanto, $\vec{u}$ pode ser escrito como uma combinação linear destes vetores (Consulte a Subseção 2.2.3).

Agora, para verificar a unicidade de $\left(\alpha,\beta,\gamma\right)$ , suponhamos que existam $\alpha^{\prime}$ , $\beta^{\prime}$ e $\gamma^{\prime}$ tais que

\vec{u}=\alpha^{\prime}\vec{a}+\beta^{\prime}\vec{b}+\gamma^{\prime}\vec{c}.

(2.51)

Subtraindo (2.51) de (2.50), obtemos

\vec{0}=(\alpha-\alpha^{\prime})\vec{a}+(\beta-\beta^{\prime})\vec{b}+(\gamma-% \gamma^{\prime})\vec{c}.

(2.52)

Como $\vec{a}$ , $\vec{b}$ e $\vec{c}$ são l.i., segue que²²2Pela definição de vetores linearmente independentes, consultemos Seção 2.2.

\alpha-\alpha^{\prime}=0,\leavevmode\nobreak\ \beta-\beta^{\prime}=0,% \leavevmode\nobreak\ \gamma-\gamma^{\prime}=0,

(2.53)

i.e. $\alpha=\alpha^{\prime}$ , $\beta=\beta^{\prime}$ e $\gamma=\gamma^{\prime}$ . ∎

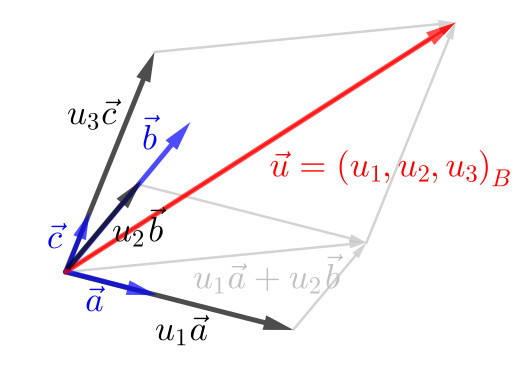
Refer to caption — Figura 2.7: Representação de um vetor $\vec{u}=(u_{1},u_{2},u_{3})_{B}$ em uma dada base $B=(\vec{a},\vec{b},\vec{c})$ .

Desta última proposição, fixada uma base $B=\left(\vec{a},\vec{b},\vec{c}\right)$ , cada vetor $\vec{u}$ é representado de forma única como combinação linear dos vetores da base, digamos

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}=u_{1}% \vec{a}+u_{2}\vec{b}+u_{3}\vec{c},

(2.54)

onde a sequência de escalares $(u_{1},u_{2},u_{3})$ é chamada de coordenadas do vetor $\vec{u}$ na base $B$ e escrevemos

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}=(u_{1% },u_{2},u_{3})_{B},

(2.55)

para expressar o vetor $\vec{u}$ nas suas coordenadas na base $B$ . Consulte a Figura 2.7.

Exemplo 2.3.1.

Fixada uma base $B=(\vec{a},\vec{b},\vec{c})$ , o vetor $\vec{u}$ de coordenadas

\vec{u}=(-2,\sqrt{2},-3)_{B}

(2.56)

é o vetor

\vec{u}=-2\vec{a}+\sqrt{2}\vec{b}-3\vec{c}.

(2.57)

2.3.1 Operações de vetores com coordenadas

Na Seção 1.2, definimos as operações de adição, subtração e multiplicação por escalar do ponto de vista geométrico. Aqui, estudamos como estas operações são definidas a partir das coordenadas de vetores.

A partir daqui, assumimos dada uma base de vetores $B=(\vec{a},\vec{b},\vec{c})$ .

Adição

Dados vetores $\vec{u}=(u_{1},u_{2},u_{3})_{B}$ e $\vec{v}=(v_{1},v_{2},v_{3})_{B}$ , i.e.

	$\displaystyle\vec{u}$	$\displaystyle=u_{1}\vec{a}+u_{2}\vec{b}+u_{3}\vec{c},$		(2.58)
	$\displaystyle\vec{v}$	$\displaystyle=v_{1}\vec{a}+v_{2}\vec{b}+v_{3}\vec{c},$		(2.59)

a adição de $\vec{u}$ com $\vec{v}$ é a soma

$\displaystyle\vec{u}+\vec{v}$	$\displaystyle=\underbrace{u_{1}\vec{a}+u_{2}\vec{b}+u_{3}\vec{c}}_{\vec{u}}$
	$\displaystyle\quad+\underbrace{v_{1}\vec{a}+v_{2}\vec{b}+v_{3}\vec{c}}_{\vec{v}}$	(2.60)
	$\displaystyle=(u_{1}+v_{1})\vec{a}+(u_{2}+v_{2})\vec{b}+(u_{3}+v_{3})\vec{c}.$	(2.61)

Ou seja,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}+\vec{% v}=(u_{1}+v_{1},u_{2}+v_{2},u_{3}+v_{3})_{B}.

(2.62)

Exemplo 2.3.2.

A adição do vetor

\vec{u}=(2,-1,-3)_{B}

(2.63)

com o vetor

\vec{v}=(-1,4,-5)_{B}

(2.64)

resulta no vetor

	$\displaystyle\vec{u}+\vec{v}$	$\displaystyle=\left(2+(-1),-1+4,-3+(-5)\right)_{B}$		(2.65)
		$\displaystyle=(1,3,-8)_{B}.$		(2.66)

Vetor oposto

O vetor oposto ao vetor $\vec{u}$ é

	$\displaystyle-\vec{u}$	$\displaystyle=-(\underbrace{u_{1}\vec{a}+u_{2}\vec{b}+u_{3}\vec{c}}_{\vec{u}})$		(2.67)
		$\displaystyle=(-u_{1})\vec{a}+(-u_{2})\vec{b}+(-u_{3})\vec{c},$		(2.68)

ou seja,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}-\vec{u}=(-u_% {1},-u_{2},-u_{3})_{B}.

(2.69)

Exemplo 2.3.3.

Dado o vetor $\vec{v}=(2,-1,-3)_{B}$ , temos

-\vec{v}=\left(-2,1,3\right)_{B}.

(2.70)

Subtração de vetores

Lembrando que subtração de $\vec{u}$ com $\vec{v}$ é definida por

\vec{u}-\vec{v}:=\vec{u}+(-\vec{v}),

(2.71)

temos que

$\displaystyle\vec{u}-\vec{v}$	$\displaystyle=(u_{1},u_{2},u_{3})_{B}$
	$\displaystyle\quad-(v_{1},v_{2},v_{3})_{B}$	(2.72)
	$\displaystyle=(u_{1},u_{2},u_{3})_{B}$
	$\displaystyle\quad+(-v_{1},-v_{2},-v_{3})_{B}$	(2.73)
	$\displaystyle=\left(u_{1}+(-v_{1}),u_{2}+(-v_{2}),u_{3}+(-v_{3})\right)$	(2.74)
	$\displaystyle=(u_{1}-v_{1},u_{2}-v_{2},u_{3}-v_{3}).$	(2.75)

Em resumo, a subtração de $\vec{u}$ com $\vec{v}$ é o vetor

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\vec{u}-\vec{% v}=(u_{1}-v_{1},u_{2}-v_{2},u_{3}-v_{3}).

(2.76)

Exemplo 2.3.4.

Sejam os vetores

\vec{u}=(2,-1,-3)_{B}

(2.77)

\vec{v}=(-1,4,-5)_{B},

(2.78)

temos que

	$\displaystyle\vec{u}-\vec{v}$	$\displaystyle=\left(2-(-1),-1-4,-3-(-5)\right)_{B}$		(2.79)
		$\displaystyle=(3,-5,2)_{B}.$		(2.80)

Multiplicação por escalar

Dado um escalar $\alpha$ e um vetor $\vec{u}$ , temos a multiplicação por escalar

	$\displaystyle\alpha\vec{u}$	$\displaystyle=\alpha(\underbrace{u_{1}\vec{a}+u_{2}\vec{b}+u_{3}\vec{c}}_{\vec% {u}})$		(2.81)
		$\displaystyle=(\alpha u_{1})\vec{a}+(\alpha u_{2})\vec{b}+(\alpha u_{3})\vec{c},$		(2.82)

ou seja,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\alpha\vec{u}% =(\alpha u_{1},\alpha u_{2},\alpha u_{3}).

(2.83)

Exemplo 2.3.5.

Dado o vetor $\vec{v}=(2,-1,-3)_{B}$ , temos

$\displaystyle-\frac{1}{3}\vec{v}$	$\displaystyle=-\frac{1}{3}(2,-1,-3)_{B}$	(2.84)
	$\displaystyle=\left(-\frac{1}{3}\cdot 2,-\frac{1}{3}\cdot(-1),-\frac{1}{3}% \cdot(-3)\right)$	(2.85)
	$\displaystyle=\left(-\frac{2}{3},\frac{1}{3},1\right)_{B}.$	(2.86)

2.3.2 Dependência linear

Vamos estudar como podemos analisar a dependência linear de vetores a partir de suas coordenadas. Assumimos fixada uma base $B=\left(\vec{a},\vec{b},\vec{c}\right)$ .

Dois vetores

Na Proposição 2.2.1, provamos que dois vetores $\vec{u}$ , $\vec{v}$ são linearmente dependentes (l.d.) se, e somente se, um for múltiplo do outro, i.e. existe um número real $\alpha$ tal que

\vec{u}=\alpha\vec{v},

(2.87)

sem perda de generalidade³³3Formalmente, pode ocorrer $\vec{v}=\beta\vec{u}$ .. Em coordenadas, temos

	$\displaystyle(u_{1},u_{2},u_{3})_{B}$	$\displaystyle=\alpha(v_{1},v_{2},v_{3})_{B}$		(2.88)
		$\displaystyle=(\alpha v_{1},\alpha v_{2},\alpha v_{3})_{B},$		(2.89)

donde

$\displaystyle u_{1}$	$\displaystyle=\alpha v_{1},$	(2.90)
$\displaystyle u_{2}$	$\displaystyle=\alpha v_{2},$	(2.91)
$\displaystyle u_{3}$	$\displaystyle=\alpha v_{3}.$	(2.92)

Concluímos que dois vetores são l.d. se, e somente se, as coordenadas de um deles forem, respectivamente, múltiplas (de mesmo fator) das coordenadas do outro.

Exemplo 2.3.6.

Estudamos os seguintes casos:

a)

Dois vetores l.d..

Sejam

$\vec{u}=(2,-1,-3)_{B}$ (2.93)

e

$\vec{v}=\left(1,-\frac{1}{2},-\frac{3}{2}\right)_{B}.$ (2.94)

Ao buscarmos por um escalar $\alpha$ tal que

$\vec{u}=\alpha\vec{v},$ (2.95)

temos

$\displaystyle\underbrace{(2,-1,-3)_{B}}_{\vec{u}}$ $\displaystyle=\alpha\underbrace{\left(1,-\frac{1}{2},-\frac{3}{2}\right)_{B}}_% {\vec{v}}$ (2.96)

$\displaystyle=\left(\alpha-\frac{\alpha}{2},-\frac{3\alpha}{2}\right)_{B},$ (2.97)

donde segue que

$\displaystyle 2=\alpha$ $\displaystyle\Rightarrow\alpha=2$ (2.98)

$\displaystyle-1=-\frac{\alpha}{2}$ $\displaystyle\Rightarrow\alpha=2$ (2.99)

$\displaystyle-3=-\frac{3\alpha}{2}$ $\displaystyle\Rightarrow\alpha=2.$ (2.100)

Concluímos que $\vec{u}=2\vec{v}$ , logo $\vec{u}$ e $\vec{v}$ são l.d..
b)

Dois vetores l.i..

Sejam, agora, os vetores

$\vec{u}=(2,-1,-3)$ (2.101)

e

$\vec{v}=\left(2,-\frac{1}{2},-\frac{3}{2}\right).$ (2.102)

Buscando por $\alpha$ tal que

$\vec{u}=\alpha\vec{v},$ (2.103)

chegamos no sistema de equações

$\left\{\begin{array}[]{l}\displaystyle 2=2\alpha\\ \displaystyle-1=-\frac{\alpha}{2}\\ \displaystyle-3=-\frac{3\alpha}{2}\end{array}\right.$ (2.104)

que não tem solução. De fato, na primeira equação $\alpha=1$ , mas na segunda $\alpha=2$ , logo não existe $\alpha$ tal que $\vec{u}=\alpha\vec{v}$ . Concluímos que $\vec{u}$ e $\vec{v}$ são l.i..

Três vetores

Na Subseção 2.2.2, estudamos que três vetores $\vec{u}$ , $\vec{v}$ e $\vec{w}$ são linearmente independentes (l.i.), quando

		$\displaystyle\alpha\vec{u}+\beta\vec{v}+\gamma\vec{w}=\vec{0}$		(2.105)
		$\displaystyle\Rightarrow\alpha=\beta=\gamma=0.$		(2.105)

Assumimos fixada uma base $B=(\vec{a},\vec{b},\vec{c})$ no espaço. Então, temos que

\alpha\vec{u}+\beta\vec{v}+\gamma\vec{w}=\vec{0}

(2.106)

é equivalente a

	$\displaystyle\alpha(u_{1},u_{2},u_{3})_{B}$
	$\displaystyle+\beta(v_{1},v_{2},v_{3})_{B}$
	$\displaystyle+\gamma(w_{1},w_{2},w_{3})_{B}$
	$\displaystyle=(0,0,0)_{B}.$		(2.107)

ou, ainda,

	$\displaystyle\left(\alpha u_{1}+\beta v_{1}+\gamma w_{1},\right.$
	$\displaystyle\left.\leavevmode\nobreak\ \alpha u_{2}+\beta v_{2}+\gamma w_{2},\right.$
	$\displaystyle\left.\leavevmode\nobreak\ \alpha u_{3}+\beta v_{3}+\gamma w_{3}% \right)_{B}$
	$\displaystyle=(0,0,0)_{B}.$		(2.108)

Esta, por sua vez, nos leva ao seguinte sistema linear

\left\{\begin{array}[]{l}u_{1}\alpha+v_{1}\beta+w_{1}\gamma=0\\ u_{2}\alpha+v_{2}\beta+w_{2}\gamma=0\\ u_{3}\alpha+v_{3}\beta+w_{3}\gamma=0\end{array}\right.

(2.109)

Agora, lembremos que um tal sistema tem solução única⁴⁴4Neste caso, a solução trivial $\alpha=\beta=\gamma=0$ se, e somente se, o determinante de sua matriz dos coeficientes é não nulo, i.e.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\begin{% vmatrix}u_{1}&v_{1}&w_{1}\\ u_{2}&v_{2}&w_{2}\\ u_{3}&v_{3}&w_{3}\end{vmatrix}\neq 0.

(2.110)

Neste caso, concluímos que $\{\vec{u},\vec{v},\vec{w}\}$ é um conjunto de vetores l.i. e, noutro caso, é l.d..

Exemplo 2.3.7.

Os vetores

\displaystyle\vec{u}

\displaystyle=(2,1,-3)_{B},\vec{v}

\displaystyle=(1,-1,2)_{B},\vec{w}

\displaystyle=(-2,1,1)_{B},

(2.111)

formam um conjunto l.d., pois

$\displaystyle\begin{vmatrix}u_{1}&v_{1}&w_{1}\\ u_{2}&v_{2}&w_{2}\\ u_{3}&v_{3}&w_{3}\end{vmatrix}$	$\displaystyle=\begin{vmatrix}2&1&-2\\ 1&-1&1\\ -3&2&1\end{vmatrix}$	(2.112)
	$\displaystyle=-2-4-3+6-4-1$	(2.113)
	$\displaystyle=-8\neq 0.$	(2.114)

2.3.3 Bases ortonormais

Uma base $B=(\vec{i},\vec{j},\vec{k})$ é dita ser ortonormal⁵⁵5Quando $\vec{u}$ ortogonal a $\vec{v}$ , denotamos $\vec{u}\perp\vec{v}$ ., quando

•

$\vec{i}$ , $\vec{j}$ e $\vec{k}$ são dois a dois ortogonais, e
•

$\|\vec{i}\|=\|\vec{j}\|=\|\vec{k}\|=1$ .

Lema 2.3.1.

(Pitágoras⁶⁶6Pitágoras de Samos, c.570, c. 495 a.C., matemático grego jônico. Fonte: Wikipédia:Pitágoras..) Se $\vec{u}\perp\vec{v}$ , então

\|\vec{u}+\vec{v}\|^{2}=\|\vec{u}\|^{2}+\|\vec{v}\|^{2}.

(2.115)

Demonstração.

Consulte o E.2.3.7. ∎

Proposição 2.3.2.

Seja $B=(\vec{i},\vec{j},\vec{k})$ uma base ortonormal e $\vec{u}=(u_{1},u_{2},u_{3})_{B}$ . Então,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\|\vec{u}\|=% \sqrt{u_{1}^{2}+u_{2}^{2}+u_{3}^{2}}.

(2.116)

Demonstração.

Temos $\|\vec{u}\|^{2}=\|u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\|^{2}$ . Seja $\pi$ um plano determinado por dadas representações de $\vec{i}$ e $\vec{j}$ . Como $\vec{i}$ , $\vec{j}$ e $\vec{k}$ são ortogonais, temos que $\vec{k}$ é ortogonal ao plano $\pi$ . Além disso, o vetor $u_{1}\vec{i}+u_{2}\vec{j}$ também admite uma representação em $\pi$ , logo $u_{1}\vec{i}+u_{2}\vec{j}$ é ortogonal a $\vec{k}$ . Do Lema 6, temos

\|\vec{u}\|^{2}=\|u_{1}\vec{i}+u_{2}\vec{j}\|^{2}+\|u_{3}\vec{k}\|^{2}.

(2.117)

Analogamente, como $u_{1}\vec{i}\perp u_{2}\vec{j}$ , temos

$\displaystyle\\|\vec{u}\\|^{2}$	$\displaystyle=\\|u_{1}\vec{i}\\|^{2}+\\|u_{2}\vec{j}\\|^{2}+\\|u_{3}\vec{k}\\|^{2}$	(2.118)
	$\displaystyle=\|u_{1}\|^{2}\\|\vec{i}\\|+\|u_{2}\|^{2}\\|\vec{j}\\|+\|u_{3}\|\\|\vec{k}\\|% ^{2}$	(2.119)
	$\displaystyle=u_{1}^{2}+u_{2}^{2}+u_{3}^{2}.$	(2.120)

Extraindo a raiz quadrada de ambos os lados da última equação, obtemos o resultado desejado. ∎

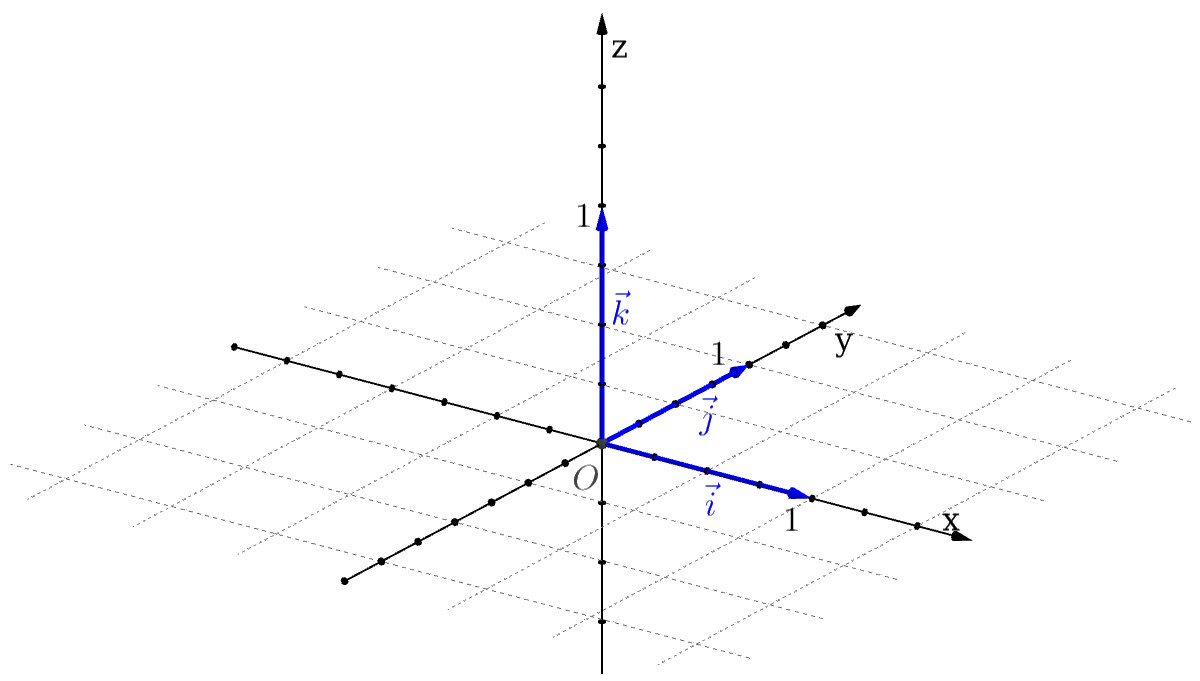
A partir daqui, salvo dito o contrário, vamos assumir fixada uma base ortonormal $B=(\vec{i},\vec{j},\vec{k})$ e, por simplicidade, escrevemos

	$\displaystyle\vec{u}$	$\displaystyle=(u_{1},u_{2},u_{3})$		(2.121)
		$\displaystyle=u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}.$		(2.122)

Exemplo 2.3.8.

A norma de $\vec{u}=\left(-1,2,-\sqrt{2}\right)$ é

	$\displaystyle\\|\vec{u}\\|$	$\displaystyle=\sqrt{(-1)^{2}+2^{2}+\left(-\sqrt{2}\right)^{2}}$		(2.123)
		$\displaystyle=\sqrt{7}.$		(2.124)

2.3.4 Exercícios resolvidos

ER 2.3.1.

Considere a base $B=(\vec{i},\vec{j},\vec{k})$ ortonormal conforme dada na Figura 2.8. Faça uma representação do vetor

\vec{u}=\left(2,\frac{1}{2},1\right)_{B}.

(2.125)

Resolução.

Primeiramente, observamos que

	$\displaystyle\vec{u}$	$\displaystyle=\left(2,\frac{1}{2},1\right)_{B}$		(2.126)
		$\displaystyle=2\vec{i}+\frac{1}{2}\vec{j}+\vec{k}.$		(2.127)

Assim sendo, podemos construir uma representação de $\vec{u}$ como dada na figura abaixo. Primeiramente, representamos os vetores $2\vec{i}$ e $\frac{1}{2}\vec{j}$ (cinza). Então, representamos o vetor $2\vec{i}+\frac{1}{2}\vec{j}$ (cinza). Por fim, temos a representação de $\vec{u}$ (vermelho).

ER 2.3.2.

Fixada uma base qualquer $B$ e dados $\vec{u}=(1,-1,2)_{B}$ e $\vec{v}=(-2,1,-1)_{B}$ , encontre o vetor $\vec{x}$ que satisfaça

\vec{u}+2\vec{x}=\vec{v}-\left(\vec{x}+\vec{u}\right).

(2.128)

Resolução.

Primeiramente, podemos manipular a equação de forma a isolarmos $\vec{x}$ como segue

	$\displaystyle\vec{u}+2\vec{x}=\vec{v}-\left(\vec{x}+\vec{u}\right)$		(2.129)
	$\displaystyle 2\vec{x}=-\vec{u}+\vec{v}-\vec{x}-\vec{u}$		(2.130)
	$\displaystyle 3\vec{x}=\vec{v}-2\vec{u}$		(2.131)
	$\displaystyle\vec{x}=\frac{1}{3}\vec{v}-\frac{2}{3}\vec{u}$		(2.132)

Agora, sabendo que $\vec{u}=(1,-1,2)_{B}$ e $\vec{v}=(-2,1,-1)_{B}$ , temos

	$\displaystyle\vec{x}=\frac{1}{3}(-2,1,-1)_{B}-\frac{2}{3}(1,-1,2)_{B}$		(2.133)
	$\displaystyle\vec{x}=\left(-\frac{2}{3},\frac{1}{3},-\frac{1}{3}\right)_{B}-% \left(\frac{2}{3},-\frac{2}{3},\frac{4}{3}\right)_{B}$		(2.134)
	$\displaystyle\vec{x}=\left(-\frac{2}{3}-\frac{2}{3},\frac{1}{3}+\frac{2}{3},-% \frac{1}{3}-\frac{4}{3}\right)$		(2.135)
	$\displaystyle\vec{x}=\left(-\frac{4}{3},1,-\frac{5}{3}\right)_{B}.$		(2.136)

ER 2.3.3.

Fixada uma base $B$ qualquer, verifique se os vetores $\vec{u}=(1,-1,2)_{B}$ , $\vec{v}=(-2,1,-1)_{B}$ e $\vec{w}=(-4,3,-5)$ também formam um base para o espaço de vetores.

Resolução.

Uma base para o espaço tridimensional $V$ é uma sequência de três vetores l.i.. Logo, para resolver a questão, basta verificar se $(\vec{u},\vec{v},\vec{w})$ é l.i.. Com base na Subseção 2.3.2, basta calcularmos o determinante da matriz cujas colunas são formadas pelas coordenadas dos vetores da sequência, i.e.

	$\displaystyle\begin{vmatrix}u_{1}&v_{1}&w_{1}\\ u_{2}&v_{2}&w_{2}\\ u_{3}&v_{3}&w_{3}\end{vmatrix}$		(2.137)
	$\displaystyle=\begin{vmatrix}1&-2&-4\\ -1&1&3\\ 2&-1&-5\end{vmatrix}$		(2.138)
	$\displaystyle=-5-4-12-(-8-3-10)$		(2.139)
	$\displaystyle=-21+21=0.$		(2.140)

Como este determinante é nulo, concluímos que $(\vec{u},\vec{v},\vec{w})$ é l.d. e, portanto, não forma uma base para $V$ .

2.3.5 Exercícios

E. 2.3.1.

Considere a base $B=(\vec{i},\vec{j},\vec{k})$ conforme dada na Figura 2.8. Faça um esboço do vetor $\vec{u}=\left(1,-1,\frac{1}{2}\right)_{B}$ .

E. 2.3.2.

Fixada uma base $B=(\vec{i},\vec{j},\vec{k})$ e sabendo que $\vec{v}=(2,0,-3)_{B}$ , escreva $\vec{v}$ como combinação linear de $\vec{i}$ , $\vec{j}$ e $\vec{k}$ .

$\vec{v}=2\vec{i}+0\vec{j}-3\vec{k}$

E. 2.3.3.

Fixada uma base $B$ qualquer e $\vec{a}=\left(0,-1,1\right)_{B}$ , $\vec{b}=\left(2,0,-1\right)_{B}$ e $\vec{c}=\left(\frac{1}{2},-\frac{1}{3},1\right)_{B}$ , calcule:

a)

$6\vec{c}$
b)

$-\vec{b}$
c)

$\vec{c}-\vec{b}$
d)

$2\vec{c}-(\vec{a}-\vec{b})$

a) $6\vec{c}=(3,-2,6)_{B}$ ; b) $-\vec{b}=(-2,0,1)_{B}$ ; c) $\vec{c}-\vec{b}=(-\frac{3}{2},-\frac{1}{3},2)_{B}$ ; d) $2\vec{c}-(\vec{a}-\vec{b})=(3,\frac{1}{3},0)_{B}$

E. 2.3.4.

Faxada uma base $B$ qualquer, verifique se os seguintes conjuntos de vetores são l.i. ou l.d..

a)

$\vec{i}=(1,0,0)_{B}$ , $\vec{j}=(0,1,0)_{B}$
b)

$\vec{a}=(1,2,0)_{B}$ , $\vec{b}=(-2,-4,1)_{B}$
c)

$\vec{a}=(1,2,0)_{B}$ , $\vec{c}=(-2,-4,0)_{B}$
d)

$\vec{i}=(1,0,0)_{B}$ , $\vec{k}=(0,0,1)_{B}$
e)

$\vec{j}=(0,1,0)_{B}$ , $\vec{k}=(0,0,1)_{B}$
f)

$\vec{a}=(1,2,-1)_{B}$ , $\vec{d}=(\frac{1}{2},1,-\frac{1}{2})_{B}$

a) l.i.; b) l.i.; c) l.d.; d) l.i.; e) l.i.; f) l.d.

E. 2.3.5.

Faxada uma base $B$ qualquer, verifique se os seguintes conjuntos de vetores são l.i. ou l.d..

a)

$\vec{i}=(1,0,0)_{B}$ , $\vec{j}=(0,1,0)_{B}$ , $\vec{k}=(0,0,1)_{B}$
b)

$\vec{a}=(0,-1,1)_{B}$ , $\vec{b}=(2,0,-1)$ , $\vec{c}=(\frac{1}{2},-\frac{1}{3},1)_{B}$
c)

$\vec{u}=(0,-1,1)_{B}$ , $\vec{v}=(2,0,-1)$ , $\vec{w}=(2,-1,0)_{B}$

a) l.i.; b) l.i.; c) l.d.

E. 2.3.6.

Seja $B=(\vec{a},\vec{b},\vec{c})$ uma base ortogonal, i.e. $\vec{a}$ , $\vec{b}$ e $\vec{c}$ são l.i. e dois a dois ortogonais. Mostre que $C=(\vec{a}/|\vec{a}|,\vec{b}/|\vec{b}|,\vec{c}/|\vec{c}|)$ é uma base ortonormal.

Segue imediatamente do fato de que $\left|\vec{u}/|u|\right|=1$ para qualquer vetor $\vec{u}\neq 0$ .

E. 2.3.7.

Demostre o Lema 6.

Sejam as representações $\vec{u}=\overrightarrow{AB}$ , $\vec{v}=\overrightarrow{BC}$ e, portanto, $\vec{u}+\vec{v}=\overrightarrow{AC}$ . Como $\vec{u}\perp\vec{v}$ , temos que o triângulo $A B C$ é retângulo e, pelo Teorema de Pitágoras, segue que $\|\overrightarrow{AC}\|^{2}=\|\overrightarrow{AB}\|^{2}+\|\overrightarrow{BC}% \|^{2}$ . Logo, $\|\vec{u}+\vec{v}\|^{2}=\|\vec{u}\|^{2}+\|\vec{v}\|^{2}$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

	$\displaystyle\underbrace{(2,-1,-3)_{B}}_{\vec{u}}$	$\displaystyle=\alpha\underbrace{\left(1,-\frac{1}{2},-\frac{3}{2}\right)_{B}}_% {\vec{v}}$		(2.96)
		$\displaystyle=\left(\alpha-\frac{\alpha}{2},-\frac{3\alpha}{2}\right)_{B},$		(2.97)

$\displaystyle 2=\alpha$	$\displaystyle\Rightarrow\alpha=2$	(2.98)
$\displaystyle-1=-\frac{\alpha}{2}$	$\displaystyle\Rightarrow\alpha=2$	(2.99)
$\displaystyle-3=-\frac{3\alpha}{2}$	$\displaystyle\Rightarrow\alpha=2.$	(2.100)

Política de uso de dados

Política de uso de dados

Vetores

2.3 Bases e coordenadas

Proposição 2.3.1.

Demonstração.

Exemplo 2.3.1.

2.3.1 Operações de vetores com coordenadas

Adição

Exemplo 2.3.2.

Vetor oposto

Exemplo 2.3.3.

Subtração de vetores

Exemplo 2.3.4.

Multiplicação por escalar

Exemplo 2.3.5.

2.3.2 Dependência linear

Dois vetores

Exemplo 2.3.6.

Três vetores

Exemplo 2.3.7.

2.3.3 Bases ortonormais

Lema 2.3.1.

Demonstração.

Proposição 2.3.2.

Demonstração.

Exemplo 2.3.8.

2.3.4 Exercícios resolvidos

ER 2.3.1.

Resolução.

ER 2.3.2.

Resolução.

ER 2.3.3.

Resolução.

2.3.5 Exercícios

E. 2.3.1.

E. 2.3.2.

E. 2.3.3.

E. 2.3.4.

E. 2.3.5.

E. 2.3.6.

E. 2.3.7.

Envie seu comentário