Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

2 Problemas Bidimensionais 2.3 Projeção 2.5 Fundamentos da análise de elementos finitos

2.4 Problema Modelo

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Em revisão

Nesta seção, aplicamos do método de elementos finitos para a equação de Poisson¹²¹²endnote: ¹²Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson. com condições de Dirichlet¹³¹³endnote: ¹³Johann Peter Gustav Lejeune Dirichlet, 1805 - 1859, matemático alemão. Fonte: Wikipédia: Johann Peter Gustav Lejeune Dirichlet.. Mais precisamente, definimos o chamdo problema forte: encontrar $u$ tal que

	$\displaystyle-\Delta u=f,\leavevmode\nobreak\ x\in\Omega:=[0,1]^{2},$		(2.29)
	$\displaystyle u=0,\leavevmode\nobreak\ x\in\partial\Omega,$		(2.30)

onde $\Delta=\partial^{2}/\partial x_{0}^{2}+\partial^{2}/\partial x_{1}^{2}$ é o operador de Laplace¹⁴¹⁴endnote: ¹⁴Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace. e $f$ é uma função dada.

2.4.1 Formulação Fraca

Em revisão

A aplicação do método de elementos finitos é construída sobre a formulação fraca do problema (2.29)-(2.30). Para a obtermos, multiplicamos (2.29) por uma função teste $v$ em um espaço adequado $V_{0}$ e integramos no domínio $\Omega$ , obtendo

-\int_{\Omega}\Delta u\,v\,dx=\int_{\Omega}fv\,dx.

(2.31)

Então, no lado esquerdo, aplicamos a fórmula de Green¹⁵¹⁵endnote: ¹⁵George Green, 1793 - 1841, matemático britânico. Fonte: Wikipédia:George Green .

\int_{\Omega}\Delta u\,v\,dx=-\int_{\Omega}\nabla u\cdot\nabla v\,dx+\int_{% \partial\Omega}\boldsymbol{n}\cdot\nabla u\,v\,ds.

(2.32)

donde temos

\int_{\Omega}\nabla u\cdot\nabla v\,dx-\int_{\partial\Omega}\boldsymbol{n}% \cdot\nabla uv\,ds=\int_{\Omega}fv\,dx.

(2.33)

Então, observando critérios de regularidade e a condição de contorno (2.30), escolhemos o espaço teste

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}V_{0}:=\{v\in H% ^{1}(\Omega):\leavevmode\nobreak\ v|_{\partial\Omega}=0\}.

(2.34)

Lembramos que $H^{1}(\Omega)=\{v:\leavevmode\nobreak\ \|v\|_{L^{2}(\Omega)}+\|\nabla v\|_{L^{% 2}(\Omega)}<\infty\}$ .

Com isso, temos o seguinte problema fraco associado a (2.29)-(2.30): encontrar $u\in V_{0}$ tal que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}a(u,v)=L(v),% \leavevmode\nobreak\ \forall v\in V_{0},

(2.35)

onde $a(u,v)$ é chamada de forma bilinear e definida por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}a(u,v):=\int_{% \Omega}\nabla u\cdot\nabla v\,dx

(2.36)

e $L(v)$ é chamada de forma linear e definida por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}L(v):=\int_{% \Omega}fv\,dx.

(2.37)

2.4.2 Formulação de Elementos Finitos

Em revisão

A formulação de elementos finitos é obtida da formulação fraca (2.35) pela aproximação do espaço teste $V_{0}$ por uma espaço de dimensão finita. Tomando uma triangulação $\mathcal{K}\subset\Omega$ e considerando o espaço contínuo dos polinômios lineares por partes

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}V_{h}:=\{v:% \leavevmode\nobreak\ v\in C^{0}(\Omega),v|_{K}\in P_{1}(K)\leavevmode\nobreak% \ \forall K\in\mathcal{K}\},

(2.38)

assumimos o espaço de elementos finitos

V_{h,0}:=\{v\in V_{h}:\leavevmode\nobreak\ v|_{\partial\Omega}=0\}.

(2.39)

Com isso, temos o seguinte problema de elementos finitos associado (2.35): encontrar $u_{h}\in V_{h,0}$ tal que

a(u_{h},v_{h})=L(v_{h}),\leavevmode\nobreak\ \forall v_{h}\in V_{h,0}.

(2.40)

Observemos que (2.40) é equivalente ao problema de encontrar $u_{h}\in V_{h,0}$ tal que

a(u_{h},\varphi_{i})=L(\varphi_{i}),

(2.41)

com $i=0,1,\cdots,n_{p}-1$ , onde $\{\varphi_{i}\}_{i=0}^{n_{i}-1}$ é a base nodal de $V_{h,0}$ e $n_{i}$ é o número de funções bases (igual ao número de nodos internos da triangulação $\mathcal{K}$ ). Ainda, como

u_{h}=\sum_{j=0}^{n_{i}-1}\xi_{j}\varphi_{j},

(2.42)

temos

	$\displaystyle a(u_{h},\varphi_{i})$	$\displaystyle=a\left(\sum_{j=0}^{n_{i}-1}\xi_{j}\varphi_{j},\varphi_{i}\right)$		(2.43)
		$\displaystyle=\sum_{j=0}^{n_{i}-1}\xi_{j}a(\varphi_{j},\varphi_{i}).$		(2.44)

Com isso, o problema de elementos finitos é equivalente a resolver o seguinte sistema linear

\sum_{j=0}^{n_{i}-1}\xi_{j}a(\varphi_{j},\varphi_{i})=L(\varphi_{i}),% \leavevmode\nobreak\ i=0,1,\cdots,n_{i}-1,

(2.45)

para as incógnitas $\xi_{j}$ , $j=0,1,\cdots,n_{i}-1$ . Ou, equivalentemente, temos sua forma matricial

A\boldsymbol{\xi}=\boldsymbol{b},

(2.46)

onde $A=[a_{i,j}]_{i,j=0}^{n_{i}-1}$ é chamada de matriz de rigidez com

a_{i,j}=a(\varphi_{j},\varphi_{i})

(2.47)

e $\boldsymbol{b}=(b_{0},b_{1},\cdots,b_{n_{i}-1})$ é o vetor de carga com

b_{i}=L(\varphi_{i}).

(2.48)

Exemplo 2.4.1.

Consideremos o seguinte problema de Poisson

	$\displaystyle-\Delta u$	$\displaystyle=100x_{0}(1-x_{0})x_{1}(1-x_{1}),\leavevmode\nobreak\ x\in\Omega:% =(0,1)\times(0,1),$		(2.49)
	$\displaystyle u$	$\displaystyle=0,\leavevmode\nobreak\ x\in\partial\Omega.$		(2.50)

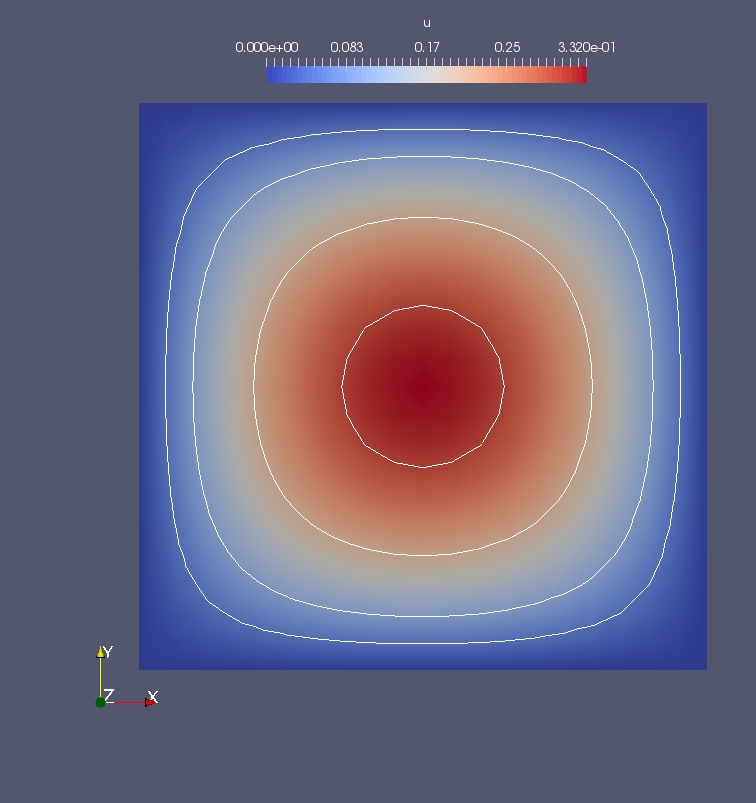
Na Figura 2.5 temos um esboço da aproximação de elementos finitos obtida em uma malha uniforme com $20\times 20$ nodos. As isolinhas correspondem aos ponto tais que $u=3\times 10^{-1},2\times 10^{-1}$ , $10^{-1}$ , $5\times 10^{-2}$ .

Refer to caption — Figura 2.5: Esboço da solução de elementos finitos do problema discutido no Exemplo 2.4.1.

Com o FEniCS, podemos computar a solução deste problema com o seguinte código:

from __future__ import print_function, division
from fenics import *
import numpy as np
import matplotlib.pyplot as plt

# malha
Nx = 20
Ny = 20
mesh = UnitSquareMesh(Nx,Ny)

# espaco
V = FunctionSpace(mesh, ’P’, 1)

# cond. contorno
def boundary(x,on_boundary):
    return on_boundary

bc = DirichletBC(V,Constant(0.0),boundary)

# f
f = Expression(’100*x[0]*(1-x[0])*x[1]*(1-x[1])’,degree=4)

# MEF problem
u = TrialFunction(V)
v = TestFunction(V)
a = dot(grad(u), grad(v))*dx
L = f*v*dx

#computa a sol
u = Function(V)
solve(a == L, u, bc)

# exportanto em vtk
vtkfile = File(’u.pvd’)
vtkfile << u

2.4.3 Exercícios

Em revisão

E. 2.4.1.

Compute uma aproximação de elementos finitos para o seguinte problema

$\displaystyle-\Delta u$	$\displaystyle=10,\leavevmode\nobreak\ x\in(0,1)\times(0,1)$	(2.51)
$\displaystyle u(x,0)$	$\displaystyle=0,\leavevmode\nobreak\ 0\leq x\leq 1,$	(2.52)
$\displaystyle u(1,y)$	$\displaystyle=0,\leavevmode\nobreak\ 0\leq y<1,$	(2.53)
$\displaystyle u(x,1)$	$\displaystyle=1,\leavevmode\nobreak\ 0\leq x\leq 1,$	(2.54)
$\displaystyle u(0,y)$	$\displaystyle=1,\leavevmode\nobreak\ 0<x\leq 1.$	(2.55)

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |