Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

5 Problema de Valor de Contorno 5 Problema de Valor de Contorno 5.2 Método de Elementos Finitos

5.1 Método de Diferenças Finitas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Consideramos o seguinte problema linear de valor de contorno (PVC)

	$\displaystyle u^{\prime\prime}+\alpha(x)u^{\prime}+\beta(x)u=f(x),\leavevmode% \nobreak\ a<x<b,$		(5.2a)
	$\displaystyle u(a)=g,$		(5.2b)
	$\displaystyle u(b)=h.$		(5.2c)

onde a incógnita é $u=u(x)$ com dada fonte $f=f(x)$ e dados parâmetros $g$ e $h$ .

A aproximação pelo Método de Diferenças Finitas (MDF) de (5.2a)-(5.2c) surge da substituição das derivadas por Fórmulas de Diferenças Finitas. De forma geral, o método pode ser dividido em três etapas: 1. discretização do domínio, 2. discretização das equações, 3. resolução do problema discreto.

1. Discretização do Domínio.

A discretização do domínio é seu particionamento em subintervalos (células computacionais) e pontos (nodos computacionais). Por simplicidade, vamos considerar apenas o caso de um particionamento uniforme. Particionamos o domínio $D=[a,b]$ em $n$ de subintervalos de tamanho de malha

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}h=\frac{b-a}{n},

(5.3)

e os nodos da partição podem ser indexados da seguinte forma

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}x_{i}=a+(i-1)h,

(5.4)

com $i=1,2,3,\dotsc,n+1$ .

2. Discretização das Equações.

Começando por (5.2a), em um nodo $x=x_{i}$ , $i=2,3,\dotsc,n$ , temos

u^{\prime\prime}(x_{i})+\alpha(x_{i})u^{\prime}(x_{i})+\beta(x_{i})u(x_{i})=f(% x_{i}).

(5.5)

Podemos substituir a segunda derivada de $u$ pela fórmula de diferenças finitas central de ordem $h^{2}$

u^{\prime\prime}(x_{i})=\underbrace{\frac{u(x_{i}-h)-2u(x_{i})+u(x_{i}+h)}{h^{% 2}}}_{D^{2}_{0,h^{2}}u(x_{i})}+O(h^{2}).

(5.6)

A primeira derivada de $u$ também pode ser substituída pela fórmula de diferenças finitas central de ordem $h^{2}$

u^{\prime}(x_{i})=\underbrace{\frac{u(x_{i}+h)-u(x_{i}-h)}{2h}}_{D_{0,h^{2}}u(% x_{i})}+O(h^{2}).

(5.7)

Agora, denotando $u_{i}\approx u(x_{i})$ , temos $u_{i-1}\approx u(x_{i}-h)$ e $u_{i+1}\approx u(x_{i}+h)$ . Substituindo as derivadas pelas fórmulas de diferenças finitas, temos de (5.5) que

		$\displaystyle\left(\frac{u_{i-1}-2u_{i}+u_{i+1}}{h^{2}}\right)+\alpha(x_{i})% \left(\frac{u_{i+1}-u_{i-1}}{2h}\right)$		(5.8)
		$\displaystyle\quad+\beta(x_{i})u_{i}+O(h^{2})=f(x_{i}),$		(5.8)

Rearranjando os termos e desconsiderando o termo do erro de truncamento, obtemos o seguinte sistema de equações lineares

		$\displaystyle\left(\frac{1}{h^{2}}-\frac{\alpha_{i}}{2h}\right)u_{i-1}+\left(% \beta_{i}-\frac{2}{h^{2}}\right)u_{i}$		(5.9)
		$\displaystyle\quad+\left(\frac{1}{h^{2}}+\frac{\alpha_{i}}{2h}\right)u_{i+1}=f% _{i},$		(5.9)

onde, usamos a notação $\alpha_{i}=\alpha(x_{i})$ , $\beta_{i}=\beta(x_{i})$ e $f_{i}=f(x_{i})$ .

Observamos que este sistema consiste em $n-1$ equações envolvendo as $n+1$ incógnitas $u_{i}$ , $i=1,2,\dotsc,n+1$ . Para fechá-lo, usamos as condições de contorno. De (5.2b), temos

u_{1}=g

(5.10)

e de (5.2c) temos

u_{n+1}=h,

(5.11)

lembrando que $u_{0}\approx u(x_{0})$ e $u_{n}\approx u(x_{n})$ .

Por fim, as equações (5.9)-(5.11) formam o seguinte problema discretizado

	$\displaystyle u_{1}=g,$		(5.12a)
	$\displaystyle\left(\frac{1}{h^{2}}-\frac{\alpha_{i}}{2h}\right)u_{i-1}+\left(% \beta_{i}-\frac{2}{h^{2}}\right)u_{i}$
	$\displaystyle\quad+\left(\frac{1}{h^{2}}+\frac{\alpha_{i}}{2h}\right)u_{i+1}=f% _{i},$		(5.12b)
	$\displaystyle u_{n+1}=h,$		(5.12c)

para $i=2,3,\dotsc,n$ .

3. Resolução do Problema Discreto.

O problema discreto (5.1) consiste em um sistema linear de $n+1$ equações com $n+1$ incógnitas. Na forma matricial temos

\eqref{cap_pvc_sec_mdf:eq:sis_mdf}A\boldsymbol{u}=\boldsymbol{b}

(5.13)

onde $\boldsymbol{u}=(u_{1},u_{2},\dotsc,u_{n+1})$ é o vetor das incógnitas, $\boldsymbol{b}=(g,f_{2},f_{3},\dotsc,f_{n},h)$ . A matriz dos coeficientes é $A=[a_{i,j}]_{i,j=1}^{n+1,n+1}$ e seus elementos não nulos são

	$\displaystyle a_{1,1}=1,$
	$\displaystyle a_{i,i-1}=\frac{1}{h^{2}}-\frac{\alpha_{i}}{2h},$		(5.14)
	$\displaystyle a_{i,i}=\beta_{i}-\frac{2}{h^{2}},$		(5.15)
	$\displaystyle a_{i,i+1}=\frac{1}{h^{2}}+\frac{\alpha_{i}}{2h},$		(5.16)
	$\displaystyle a_{n+1,n+1}=1,$		(5.17)

para $i=2,3,\dotsc,n$ .

A resolução do problema discreto se resume, a resolver o sistema $A\boldsymbol{u}=\boldsymbol{b}$ , o que pode ser feito por qualquer método numérico apropriado.

Exemplo 5.1.1.

Consideramos o seguinte PVC

	$\displaystyle-u^{\prime\prime}=\pi^{2}\operatorname{sen}(\pi x),\leavevmode% \nobreak\ 0<x<1,$		(5.18)
	$\displaystyle u(0)=0,$		(5.19)
	$\displaystyle u(1)=0.$		(5.20)

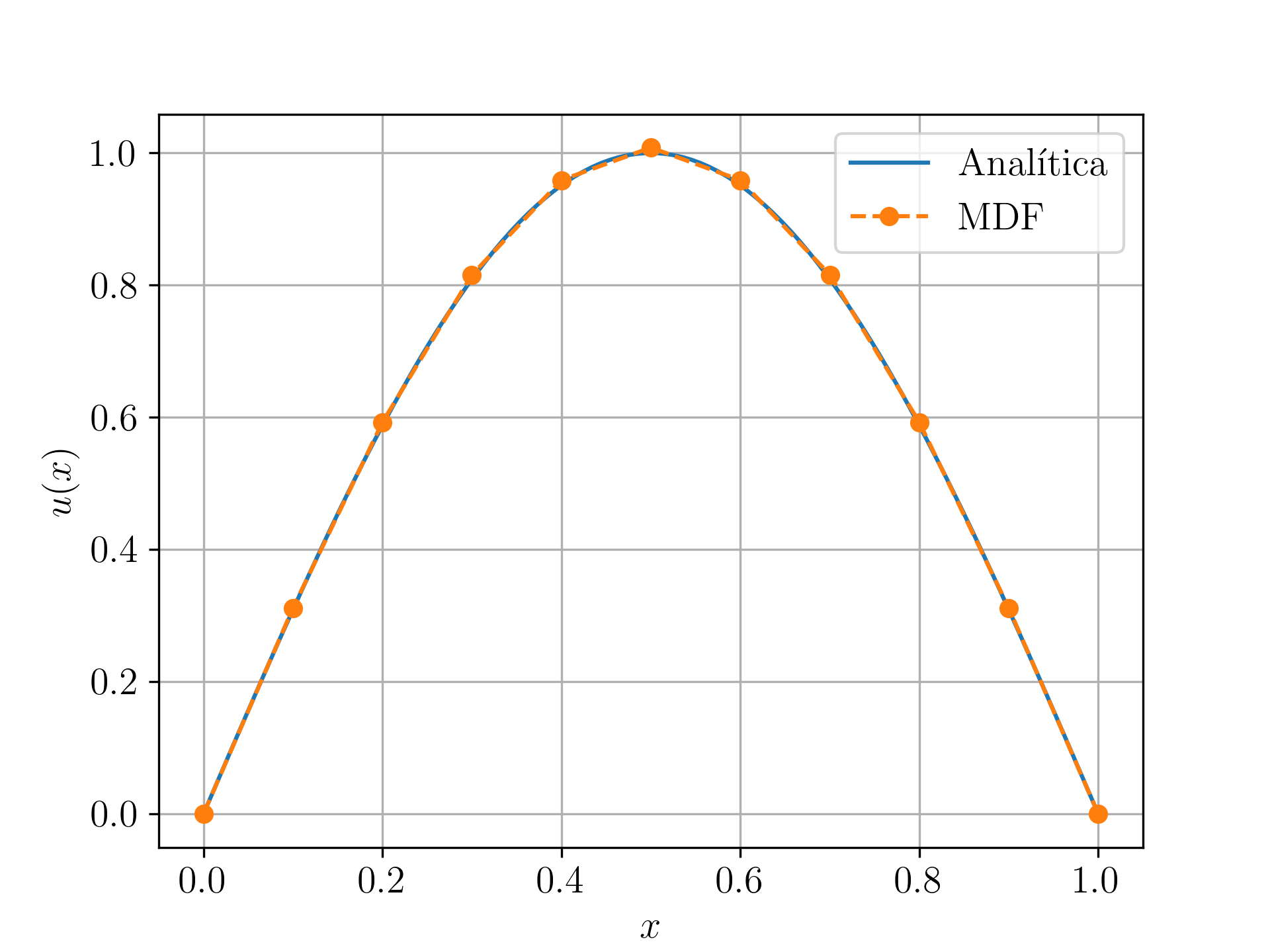
Refer to caption — Figura 5.1: Resultado referente ao Exemplo 5.1.1.

A solução analítica deste problema é $u(x)=\operatorname{sen}(\pi x)$ . Usando o MDF como acima, encontramos o problema discreto

$\displaystyle u_{1}$	$\displaystyle=0,$	(5.21a)
$\displaystyle-\frac{1}{h^{2}}u_{i-1}+\frac{2}{h^{2}}u_{i}-\frac{1}{h^{2}}u_{i+1}$	$\displaystyle=\pi^{2}\operatorname{sen}(\pi x_{i}),$	(5.21b)
$\displaystyle u_{n+1}$	$\displaystyle=0,$	(5.21c)

com tamanho de malha $h=1/n$ e nodos $x_{i}=(i-1)h$ indexados por $i=1,2,\dotsc,n+1$ .

Tabela 5.1: Resultados referentes ao Exemplo 5.1.1.

$h$	$\\|\tilde{u}-u\\|_{L^{2}}$
$1.0\mathrm{e}\!-\!1$	$1.8\mathrm{e}\!-\!2$
$5.0\mathrm{e}\!-\!2$	$6.5\mathrm{e}\!-\!3$
$2.5\mathrm{e}\!-\!2$	$2.3\mathrm{e}\!-\!3$
$1.0\mathrm{e}\!-\!3$	$5.8\mathrm{e}\!-\!4$

Resolvendo este sistema com $h=10^{-1}$ obtemos a solução numérica apresentada na Figura 5.1. Ainda, na Tabela 5.1 temos a comparação na norma $L^{2}$ da solução numérica $\tilde{\boldsymbol{u}}$ com a solução analítica $\boldsymbol{u}=(u(x_{i}))_{i=1}^{n+1}$ para diferentes escolhas de $h$ .

Código 16: pvc_mdf.py

⬇

1import numpy as np

3# malha

4n = 10

5h = 1./n

6xx = np.linspace(0., 1., n+1)

8# fonte

9def f(x):

10 return np.pi**2*np.sin(np.pi*x)

12# prob discreto

13A = np.zeros((n+1, n+1))

14b = np.empty(n+1)

16# c.c. x = 0.

17A[0,0] = 1.

18b[0] = 0.

20# pts internos

21for i in range(1,n):

22 A[i,i-1] = -1./h**2

23 A[i,i] = 2./h**2

24 A[i,i+1] = -1./h**2

25 b[i] = f(xx[i])

27# c.c. x = 1.

28A[n,n] = 1.

29b[n] = 0.

31# resol

32u = npla.solve(A, b)

5.1.1 Exercícios

E. 5.1.1.

Considere o PVC

	$\displaystyle-u^{\prime\prime}=\pi^{2}\cos(\pi x),\leavevmode\nobreak\ 0<x<1,$		(5.22)
	$\displaystyle u(0)=1,$		(5.23)
	$\displaystyle u(1)=-1.$		(5.24)

A solução analítica deste problema é $u(x)=\cos(\pi x)$ . Use o MDF para computar aproximações numéricas $\tilde{\boldsymbol{u}}_{h}$ com tamanhos de malha $h=10^{-1},10^{-2},10^{-3},10^{-4}$ e verifique o erro absoluto $\varepsilon_{\text{abs}}:=\|\tilde{\boldsymbol{u}}_{h}-\boldsymbol{u}\|$ .

Resposta.

$h$	$\\|\tilde{u}-u\\|_{L^{2}}$
$10^{-1}$	$3.9\mathrm{e}\!-\!3$
$10^{-2}$	$1.2\mathrm{e}\!-\!4$
$10^{-3}$	$3.9\mathrm{e}\!-\!6$
$10^{-4}$	$1.2\mathrm{e}\!-\!7$

E. 5.1.2.

Considere o PVC

	$\displaystyle-u^{\prime\prime}=2,\leavevmode\nobreak\ -1<x<1,$		(5.25)
	$\displaystyle u(-1)=0,$		(5.26)
	$\displaystyle u(1)=0.$		(5.27)

A solução analítica deste problema é $u(x)=1-x^{2}$ . Use o MDF com $n=20$ subintervalos na malha e verifique o erro absoluto $\varepsilon_{\text{abs}}:=\|\tilde{\boldsymbol{u}}_{h}-\boldsymbol{u}\|$ . Por que o erro está próximo precisão de máquina? Justifique sua resposta.

Resposta.

$\varepsilon_{\text{abs}}=3.1\mathrm{e}\!-\!14$ .

E. 5.1.3.

Considere o seguinte PVC

	$\displaystyle-u^{\prime\prime}+u^{\prime}=f(x),\leavevmode\nobreak\ -1<x<1,$		(5.28a)
	$\displaystyle u(-1)=0,$		(5.28b)
	$\displaystyle u^{\prime}(1)=0,$		(5.28c)

onde

f(x)=\left\{\begin{array}[]{ll}1&,x\leq 0\\ 0&,x>0\end{array}\right.

(5.29)

Use uma aproximação adequada pelo método de diferenças finitas para obter o valor aproximado de $u(0)$ com precisão de $2$ dígitos significativos.

Resposta.

$2,7\mathrm{e}\!-\!1$

E. 5.1.4.

Considere o PVC

	$\displaystyle-u^{\prime\prime}=\pi^{2}\cos(\pi x),\leavevmode\nobreak\ 0<x<1,$		(5.30)
	$\displaystyle u(0)=1,$		(5.31)
	$\displaystyle u^{\prime}(1)=0.$		(5.32)

A solução analítica deste problema é $u(x)=\cos(\pi x)$ . Aplique o MDF para computar aproximações numéricas usando a:

a)

fórmula de diferenças finitas $D_{-,h}u(x)$ no contorno $x=1$ .
b)

fórmula de diferenças finitas $D_{-,h^{2}}u(x)$ no contorno $x=1$ .

Quais das duas produz o resultado mais preciso? Justifique sua resposta.

Resposta.

b) resultado mais preciso.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |