Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

3 Métodos para Sistemas Lineares 3.3 Métodos de Jacobi e de Gauss-Seidel 3.5 Método do Gradiente Conjugado

3.4 Método do Gradiente

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Começamos observando que se $A$ é uma matriz $n\times n$ positiva definida⁴⁰⁴⁰endnote: ⁴⁰ $A$ é simétrica e $\boldsymbol{x}^{T}A\boldsymbol{x}>0$ para todo $\boldsymbol{x}\neq 0$ ., temos que $\boldsymbol{x}\in\mathbb{R}^{n}$ é solução de

A\boldsymbol{x}=\boldsymbol{b}

(3.440)

se, e somente se, $\boldsymbol{x}$ é solução do seguinte problema de minimização

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\min_{% \boldsymbol{y}\in\mathbb{R}^{n}}\left\{f(\boldsymbol{y}):=\frac{1}{2}% \boldsymbol{y}^{T}A\boldsymbol{y}-\boldsymbol{y}^{T}\boldsymbol{b}\right\}.

(3.441)

De fato, sejam $\boldsymbol{x}$ a solução de (3.440) e $\boldsymbol{y}$ a solução de (3.441), então

$\displaystyle f(\boldsymbol{y})$	$\displaystyle:=\frac{1}{2}\boldsymbol{y}^{T}A\boldsymbol{y}-\boldsymbol{y}^{T}% \boldsymbol{b}$	(3.442)
	$\displaystyle=\frac{1}{2}\boldsymbol{y}^{T}A\boldsymbol{y}-\boldsymbol{y}^{T}% \boldsymbol{b}+{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{% 0,0,1}\pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\frac{1}% {2}\boldsymbol{x}^{T}A\boldsymbol{x}-+\frac{1}{2}\boldsymbol{x}^{T}A% \boldsymbol{x}}$	(3.443)
	$\displaystyle=\frac{1}{2}(\boldsymbol{x}-\boldsymbol{y})^{T}A(\boldsymbol{x}-% \boldsymbol{y})-\frac{1}{2}\boldsymbol{x}^{T}A\boldsymbol{x}$	(3.444)

O segundo termo é independente de $\boldsymbol{y}$ e, como $A$ é positiva definida, temos

\frac{1}{2}(\boldsymbol{x}-\boldsymbol{y})^{T}A(\boldsymbol{x}-\boldsymbol{y})% \geq 0.

(3.445)

Logo, o mínimo de $f$ ocorre quando $\boldsymbol{x}-\boldsymbol{y}=\boldsymbol{0}$ , i.e. $\boldsymbol{y}=\boldsymbol{x}$ .

A iteração do Método do Gradiente tem a forma

	$\displaystyle\boldsymbol{x}^{(0)}$	$\displaystyle=\text{aprox. inicial},$		(3.446)
	$\displaystyle\boldsymbol{x}^{(k+1)}$	$\displaystyle=\boldsymbol{x}^{(k)}+\alpha_{k}\boldsymbol{d}^{(k)},$		(3.446)

para $k=0,1,2,\ldots$ , onde $\alpha_{k}>0$ é o tamanho do passo e $\boldsymbol{d}^{(k)}$ é o vetor direção de busca.

Para escolhermos a direção $\boldsymbol{d}^{(k)}$ , tomamos a fórmula de Taylor de $f$ em torno da aproximação $\boldsymbol{x}^{(k)}$

f\left(\boldsymbol{x}^{(k+1)}\right)=f\left(\boldsymbol{x}^{(k)}\right)+\alpha% ^{(k)}\nabla f\left(\boldsymbol{x}^{(k)}\right)\cdot\boldsymbol{d}^{(k)}+\epsilon,

(3.447)

onde $\nabla f$ denota o gradiente de $f$ , i.e.

	$\displaystyle\nabla f(\boldsymbol{x})$	$\displaystyle:=\left(\frac{\partial f}{\partial x_{1}}(\boldsymbol{x}),\frac{% \partial f}{\partial x_{2}}(\boldsymbol{x}),\dotsc,\frac{\partial f}{\partial x% _{n}}(\boldsymbol{x})\right)$		(3.448)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\nabla f(% \boldsymbol{x})$	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}=A\boldsymbol{% x}^{(k)}-\boldsymbol{b}.$		(3.449)

De , segue que se

\nabla f\left(\boldsymbol{x}^{(k)}\right)\cdot\boldsymbol{d}^{(k)}<0,

(3.450)

então $f\left(\boldsymbol{x}^{(k+1)}\right)<f\left(\boldsymbol{x}^{(k)}\right)$ , para $\alpha^{(k)}$ suficientemente pequeno. Em particular, podemos escolher

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\boldsymbol{d}% ^{(k)}=-\nabla f\left(\boldsymbol{x}^{(k)}\right),

(3.451)

se $\nabla f(\boldsymbol{x}^{(k)})\neq 0$ .

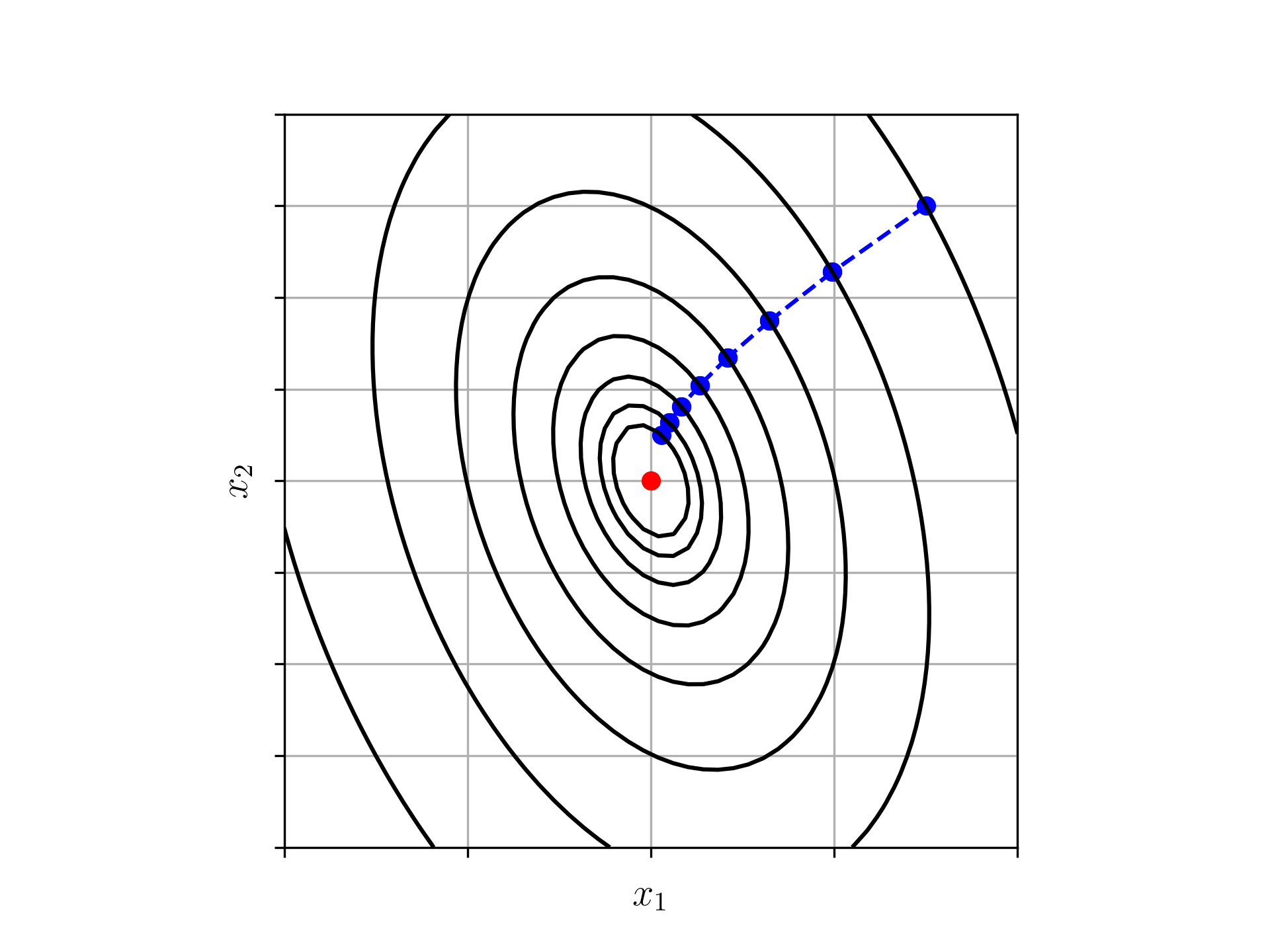
Refer to caption — Figura 3.1: Iterações do Método do Gradiente para sistemas lineares. Linha: $\|b-Ax\|$ . Pontos: $\boldsymbol{x}^{(k)}$ .

Do exposto acima, temos a iteração do Método do Gradiente

	$\displaystyle\boldsymbol{x}^{(0)}$	$\displaystyle=\text{aprox. inicial}$		(3.452)
	$\displaystyle\boldsymbol{x}^{(k+1)}$	$\displaystyle=\boldsymbol{x}^{(k)}+\alpha^{(k)}\boldsymbol{r}^{(k)}$		(3.452)

com $k=0,1,2,\ldots$ , onde $\boldsymbol{r}^{(k)}$ é o resíduo

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\boldsymbol{r}% ^{(k)}=\boldsymbol{b}-A\boldsymbol{x}^{(k)}.

(3.453)

Exemplo 3.4.1.

Consideramos o sistema $Ax=b$ com

	$\displaystyle A$	$\displaystyle=\begin{bmatrix}2&-1&0&0\\ -1&2&-1&0\\ 0&-1&2&-1\\ 0&0&-1&2\end{bmatrix},$		(3.458)
	$\displaystyle b$	$\displaystyle=\begin{bmatrix}-3\\ 2\\ 2\\ -3\end{bmatrix}.$		(3.463)

Na Tabela 3.3 temos os resultados do emprego do método do gradiente com $\boldsymbol{x}^{(1)}=(0,0,0,0)$ e com passo constante $\alpha^{(k)}\equiv 0.5$ .

Tabela 3.3: Resultados referentes ao Exemplo 3.4.1.

k	$\boldsymbol{x}^{(k)}$	$\\|A\boldsymbol{x}^{(k)}-\boldsymbol{b}\\|$
0	$(0.0,0.0,0.0,0.0)$	$5.1\mathrm{e}\!+\!0$
1	$(-1.5,1.0,1.0,-1.5)$	$1.6\mathrm{e}\!+\!0$
2	$(-1.0,0.8,0.8,-1.0)$	$5.0\mathrm{e}\!-\!1$
3	$(-1.1,0.9,0.9,-1.1)$	$1.8\mathrm{e}\!-\!1$
4	$(-1.1,0.9,0.9,-1.1)$	$8.8\mathrm{e}\!-\!2$
5	$(-1.1,0.9,0.9,-1.1)$	$6.2\mathrm{e}\!-\!2$
6	$(-1.0,0.9,0.9,-1.0)$	$4.9\mathrm{e}\!-\!2$
7	$(-1.0,0.9,0.9,-1.0)$	$4.0\mathrm{e}\!-\!2$
8	$(-1.0,0.9,0.9,-1.0)$	$3.2\mathrm{e}\!-\!2$
9	$(-1.0,1.0,1.0,-1.0)$	$2.6\mathrm{e}\!-\!2$
10	$(-1.0,1.0,1.0,-1.0)$	$2.1\mathrm{e}\!-\!2$

Código 10: mg.py

⬇

1import numpy as np

2import numpy.linalg as npla

4def mg(A, b, x0, alpha=1e-2,

5 maxiter=100, atol=1.49e-8, rtol=1.49e-8):

7 n = b.size

8 x = x0.copy()

9 res = b - A@x

10 nres = npla.norm(res)

11 print(f'0: {x}, nres = {nres:.1e}')

12 info = -1

13 for k in range(maxiter):

14 x = x + alpha*res

16 res = b - A@x

17 nres = npla.norm(res)

19 print(f'{k+1}: {x}, nres = {nres:.1e}')

21 if (nres <= max(atol, rtol*npla.norm(b))):

22 info = 0

23 break

25 return x, info

27# matriz coefs

28A = np.array([[2., -1., 0., 0.],

29 [-1., 2., -1., 0.],

30 [0., -1., 2., -1.],

31 [0., 0., -1., 2.]])

32# vetor constante

33b = np.array([-3., 2., 2., -3.])

35# aprox. inicial

36x0 = np.zeros_like(b)

38x, info = mg(A, b, x0, alpha=0.5)

3.4.1 Escolha do Passo

Para a escolha do passo, podemos usar o Método da Pesquisa Linear. A ideia é escolher o passo $\alpha^{(k)}$ tal que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}f\left(% \boldsymbol{x}^{(k)}+\alpha^{(k)}\boldsymbol{r}^{(k)}\right)=\min_{\alpha>0}f% \left(\boldsymbol{x}^{(k)}+\alpha\boldsymbol{r}^{(k)}\right).

(3.464)

Observando que $f(\boldsymbol{x}^{(k)}+\alpha\boldsymbol{r}^{(k)})$ é função apenas de $\alpha$ , temos que seu mínimo ocorre em seu ponto crítico, i.e.

	$\displaystyle\frac{d}{d\alpha}f\left(\boldsymbol{x}^{(k)}+\alpha\boldsymbol{r}% ^{(k)}\right)=0$		(3.465)
	$\displaystyle\nabla f\left(\boldsymbol{x}^{(k+1)}\right)\cdot\frac{d}{d\alpha}% \left(\boldsymbol{x}^{(k)}+\alpha\boldsymbol{r}^{(k)}\right)=0$		(3.466)
	$\displaystyle\nabla f(\boldsymbol{x}^{(k+1)})\cdot\boldsymbol{r}^{(k)}=0,$		(3.467)
	$\displaystyle\left[A\left(\boldsymbol{x}^{(k)}+\alpha^{(k)}\boldsymbol{r}^{(k)% }\right)-b\right]\cdot\boldsymbol{r}^{(k)}=0,$		(3.468)
	$\displaystyle\left(A\boldsymbol{x}^{(k)}-\boldsymbol{b}\right)\cdot\boldsymbol% {r}^{(k)}+\alpha^{(k)}\boldsymbol{r}^{(k)}\cdot A\boldsymbol{r}^{(k)}=0,$		(3.469)

donde

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\alpha^{(k)}=% \frac{\boldsymbol{r}^{(k)}\cdot\boldsymbol{r}^{(k)}}{\boldsymbol{r}^{(k)}\cdot A% \boldsymbol{r}^{(k)}}.

(3.470)

Exemplo 3.4.2.

Consideramos o sistema $Ax=b$ com

	$\displaystyle A$	$\displaystyle=\begin{bmatrix}2&-1&0&0\\ -1&2&-1&0\\ 0&-1&2&-1\\ 0&0&-1&2\end{bmatrix},$		(3.475)
	$\displaystyle b$	$\displaystyle=\begin{bmatrix}-3\\ 2\\ 2\\ -3\end{bmatrix}.$		(3.480)

Na Tabela 3.4 temos os resultados do emprego do método do gradiente com $\boldsymbol{x}^{(1)}=(0,0,0,0)$ e com passo escolhido conforme (3.470).

Tabela 3.4: Resultados referentes ao Exemplo LABEL:cap_sislin_sec_metg:ex:metg_alpha.

k	$\boldsymbol{x}^{(k)}$	$\alpha^{(k)}$	$\\|A\boldsymbol{x}^{(k)}-\boldsymbol{b}\\|$
$0$	$(0.0,0.0,0.0,0.0)$	$3.8\mathrm{e}\!-\!1$	$5.1\mathrm{e}\!+\!0$
$1$	$(-1.1,0.8,0.8,-1.1)$	$2.6\mathrm{e}\!+\!0$	$1.5\mathrm{e}\!-\!1$
$2$	$(-1.0,1.0,1.0,-1.0)$	$3.8\mathrm{e}\!-\!1$	$3.0\mathrm{e}\!-\!2$
$3$	$(-1.0,1.0,1.0,-1.0)$	$2.6\mathrm{e}\!+\!0$	$8.8\mathrm{e}\!-\!4$
$4$	$(-1.0,1.0,1.0,-1.0)$	$3.8\mathrm{e}\!+\!0$	$1.8\mathrm{e}\!-\!4$
$5$	$(-1.0,1.0,1.0,-1.0)$	$2.6\mathrm{e}\!+\!0$	$5.2\mathrm{e}\!-\!6$

⬇

1import numpy as np

2import numpy.linalg as npla

4def mg_pl(A, b, x0,

5 maxiter=100, atol=1.49e-8, rtol=1.49e-8):

7 n = b.size

8 x = x0.copy()

9 res = b - A@x

10 alpha = np.dot(res, res)/np.dot(res, A@res)

11 nres = npla.norm(res)

12 print(f'0: {x}, alpha = {alpha}, nres = {nres:.1e}')

13 info = -1

14 for k in range(maxiter):

15 x = x + alpha*res

17 res = b - A@x

18 alpha = np.dot(res, res)/np.dot(res, A@res)

19 nres = npla.norm(res)

21 print(f'{k+1}: {x}, alpha = {alpha}, nres = {nres:.1e}')

23 if (nres <= max(atol, rtol*npla.norm(b))):

24 info = 0

25 break

27 return x, info

29# matriz coefs

30A = np.array([[2., -1., 0., 0.],

31 [-1., 2., -1., 0.],

32 [0., -1., 2., -1.],

33 [0., 0., -1., 2.]])

34# vetor constante

35b = np.array([-3., 2., 2., -3.])

37# aprox. inicial

38x0 = np.zeros_like(b)

40x, info = mg_pl(A, b, x0)

3.4.2 Exercícios

E. 3.4.1.

Considere o sistema linear $A\boldsymbol{x}=\boldsymbol{b}$ com

	$\displaystyle A$	$\displaystyle=\begin{bmatrix}2&-1&0&0\\ -1&2&-1&0\\ 0&-1&2&-1\\ 0&0&-1&2\end{bmatrix},$		(3.485)
	$\displaystyle b$	$\displaystyle=\begin{bmatrix}5\\ -7\\ 6\\ -1\end{bmatrix}.$		(3.490)

Por tentativa e erro, encontre um valor para $\alpha$ tal que o Método do Gradiente converge para solução do sistema em menos de $80$ iterações. Use

\boldsymbol{x}^{(0)}=\boldsymbol{0}

(3.491)

como aproximação inicial e assuma o critério de parada

\|\boldsymbol{r}\|\leq\max\{\texttt{tol},\texttt{tol}\|\boldsymbol{b}\|\},

(3.492)

onde $\boldsymbol{r}$ é o resíduo do sistema e $\texttt{tol}=1.49\mathrm{e}\!-\!8$ .

Resposta.

$alpha=4.9\mathrm{e}\!-\!1$ , $\boldsymbol{x}=\left(2.0,-1.0,3.0,1.0\right)$

E. 3.4.2.

Considere o sistema linear $A\boldsymbol{x}=\boldsymbol{b}$ com

	$\displaystyle A$	$\displaystyle=\begin{bmatrix}2&-1&1&0\\ -1&2&-1&0\\ 1&-1&3&-1\\ 0&0&-1&2\end{bmatrix},$		(3.497)
	$\displaystyle b$	$\displaystyle=\begin{bmatrix}-8\\ 9\\ -10\\ 5\end{bmatrix}.$		(3.502)

Por tentativa e erro, encontre um valor para $\alpha$ tal que o Método do Gradiente converge para solução do sistema em menos de $50$ iterações. Use

\boldsymbol{x}^{(0)}=\boldsymbol{0}

(3.503)

como aproximação inicial e assuma o critério de parada

\|\boldsymbol{r}\|\leq\max\{\texttt{tol},\texttt{tol}\|\boldsymbol{b}\|\},

(3.504)

onde $\boldsymbol{r}$ é o resíduo do sistema e $\texttt{tol}=1.49\mathrm{e}\!-\!8$ .

Resposta.

$alpha=3.6\mathrm{e}\!-\!1$ , $\boldsymbol{x}=\left(-2.0,3.0,-1.0,2.0\right)$

E. 3.4.3.

Considere o sistema linear dado no Exercício 3.4.1. Utilizando a mesma aproximação inicial e tolerância, aplique o Método do Gradiente com Pesquisa Linear. Quantas iterações são necessárias até a convergência e qual o valor médio de $\alpha^{(k)}$ utilizado durante as iterações?

Resposta.

$75$ , $\overline{\alpha}=5.0\mathrm{e}\!-\!1$

E. 3.4.4.

Considere o sistema linear dado no Exercício 3.4.2. Utilizando a mesma aproximação inicial e tolerância, aplique o Método do Gradiente com Pesquisa Linear. Quantas iterações são necessárias até a convergência e qual o valor médio de $\alpha^{(k)}$ utilizado durante as iterações?

Resposta.

$35$ , $\overline{\alpha}=3.7\mathrm{e}\!-\!1$

E. 3.4.5.

Considere o problema de Laplace

	$\displaystyle-$	$\displaystyle u_{xx}=2,\quad 0<x<1,$		(3.505)
		$\displaystyle u(0)=u(1)=0.$		(3.506)

A discretização pelo Método das Diferenças Finitas em uma malha uniforme $x_{i}=ih$ , $i=0.1,\dotsc,n$ , $h=1/(n-1)$ , leva ao seguinte sistema linear

	$\displaystyle u_{1}=0$		(3.507)
	$\displaystyle-\frac{1}{h^{2}}u_{i-1}+\frac{2}{h^{2}}u_{i}-\frac{1}{h^{2}}u_{i+% 1}=2,$		(3.508)
	$\displaystyle u_{n}=0$		(3.509)

onde $u_{i}\approx u(x_{i})$ . Com $u^{(0)}=\boldsymbol{0}$ , aplique o Método do Gradiente com Pesquisa Linear para computar a solução deste sistema quando $n=10,20,40,80$ . Quantas iterações são necessárias para obter-se a convergência do método com critério de convergência

\|\boldsymbol{r}\|\leq\texttt{tol},

(3.510)

onde, $\boldsymbol{r}:=\boldsymbol{b}-A\boldsymbol{x}$ é o resíduo e $\texttt{tol}=1e-4$ .

Resposta.

$n$	$k$
$10$	$214$
$20$	$918$
$40$	$3840$
$80$	$15910$

Análise Numérica

E. 3.4.6.

Sendo $f$ dada em (3.441), mostre que

\nabla f\left(\boldsymbol{x}\right)=-\boldsymbol{r},

(3.511)

com, $\boldsymbol{r}:=b-A\boldsymbol{x}$ o resíduo do sistema $A\boldsymbol{x}=\boldsymbol{b}$ .

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |