| | | | |

1.4 Limites no infinito

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Limites no infinito descrevem a tendência de uma dada função f⁢(x) quando x→−∞ ou x→∞. Dizemos que o limite de f⁢(x) é L quando x tende a −∞, se os valores de f⁢(x) são arbitrariamente próximos de L para todos os valores de x suficientemente pequenos. Neste caso, escrevemos

limx→−∞f⁢(x)=L. (1.148)

Veja a Figura 1.7.

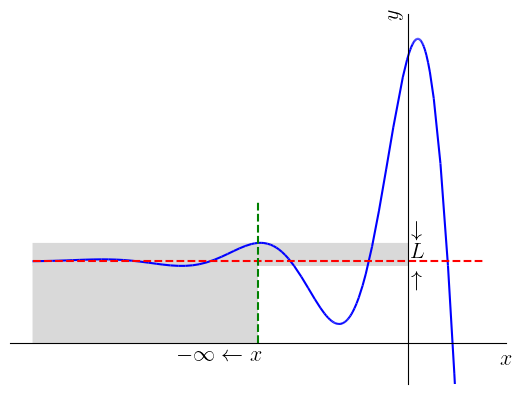
Refer to caption
Figura 1.7: Ilustração da noção de limite de uma função quando x→−∞.

Analogamente, dizemos que o limite de f⁢(x) é L quando x tende ∞, se os valores de f⁢(x) são arbitrariamente próximos de L para todos os valores de x suficientemente grandes. Neste caso, escrevemos

limx→∞f⁢(x)=L. (1.149)

Veja a Figura 1.8.

Refer to caption
Figura 1.8: Ilustração da noção de limite de uma função quando x→∞.
Exemplo 1.4.1.

Vamos inferir os limites de f⁢(x)=1/x para x→−∞ e x→∞. A Figura 1.9 é um esboço do gráfico desta função.

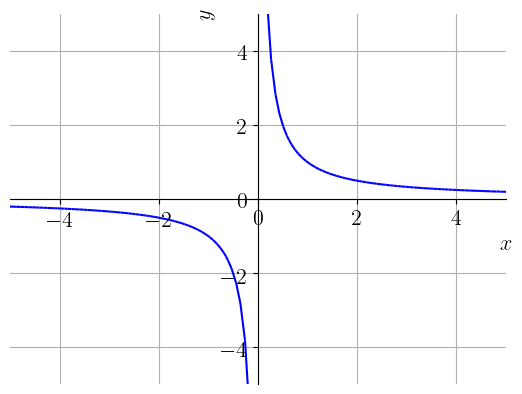
Refer to caption
Figura 1.9: Esboço do gráfico de f⁢(x)=1/x.

Observamos que quanto menores os valores de x, mais próximos de 0 são os valores de f⁢(x)=1/x. Daí, inferimos que

limx→−∞1x=0. (1.150)

Também, quanto maiores os valores de x, mais próximos de 0 são os valores de f⁢(x)=1/x. Com isso, podemos concluir que

limx→∞1x=0. (1.151)

Podemos computar estes limites com o Python+SymPy, usando os seguintes comandos:

Código 13: Python
⬇
1  >>> from sympy import *
2  >>> x = Symbol("x")
3  >>> limit(1/x, x, -oo)
4  0
5  >>> limit(1/x, x, oo)
6  0
Observação 1.4.1.

(Regras para o cálculo de limites no infinito) Supondo que L, M e k são números reais e

limx→±∞f⁢(x)=L (1.152)

e

limx→±∞g⁢(x)=M. (1.153)

Então, temos as seguintes regras para limites no infinito:

  • •

    Regra da multiplicação por escalar

    limx→±∞k⁢f⁢(x)=k⁢L (1.154)
  • •

    Regra da soma/diferença

    limx→±∞(f⁢(x)±g⁢(x))=L±M (1.155)
  • •

    Regra do produto

    limx→±∞f⁢(x)⁢g⁢(x)=L⁢M (1.156)
  • •

    Regra do quociente

    limx→±∞f⁢(x)g⁢(x)=LM,M≠0. (1.157)
  • •

    Regra da potenciação

    limx→±∞(f⁢(x))k=Lk, se ⁢Lk∈ℝ. (1.158)
Exemplo 1.4.2.
limx→∞1x2+1 (1.159)
=limx→∞1x2+limx→∞1 (1.160)
=(limx→∞1x)2+1 (1.161)
=02+1=1. (1.162)
Exemplo 1.4.3.

Consideramos o seguinte caso

limx→∞x3−2⁢x+12−3⁢x3. (1.163)

Observamos que não podemos usar a regra do quociente diretamente, pois, por exemplo, não existe o limite do numerador. A alternativa é multiplicar e dividir por 1/x3 (grau dominante), obtendo

limx→∞x3−2⁢x+12−3⁢x3 (1.164)
=limx→∞x3−2⁢x+12−3⁢x3⋅1x31x3 (1.165)
=limx→∞x3x3−2⁢xx3+1x32x3−3⁢x3x3 (1.166)
=limx→∞1−2x2+1x32x3−3 (1.167)

Então, aplicando as regras do quociente, da soma/subtração e da multiplicação por escalar, temos

limx→∞x3−2⁢x+12−3⁢x3 (1.168)
=limx→∞1−2x2+1x32x3−3 (1.169)
=−13. (1.170)
Proposição 1.4.1.

Dados dois polinômios

p⁢(x)=an⁢xn+an−1⁢xn−1+⋯+a0 (1.171)
q⁢(x)=bm⁢xm+bm−1⁢xm−1+⋯+b0 (1.172)

temos

limx→±∞p⁢(x)q⁢(x)=limx→±∞an⁢xnbm⁢xm. (1.173)
Demonstração.

Consulte o Exercício 1.4.8. ∎

Exemplo 1.4.4.

Retornando ao Exemplo 1.4.3, temos

limx→∞x3−2⁢x+12−3⁢x3 (1.174)
=limx→∞x3−3⁢x3 (1.175)
=−13. (1.176)

A ideia utilizada no Exemplo 1.4.3, também pode ser útil em limites no infinito envolvendo funções raiz.

Exemplo 1.4.5.

Vamos calcular

limx→∞x2−xx+1. (1.177)

A ideia é multiplicar em cima e em baixo por 1/x2. Seguimos

limx→∞x2−xx+1⁢1x21x2 (1.178)
=limx→∞x2−xx2x+1x2 (1.179)
=limx→∞1−1xx+1|x| (1.180)
=limx→∞1−1xx+1x (1.181)
=limx→∞1−1x1+1x (1.182)
=11=1 (1.183)

1.4.1 Assíntotas horizontais

A reta y=L é dita assíntota horizontal ao gráfico da função y=f⁢(x) se

limx→−∞f⁢(x)=L (1.184)

ou

limx→∞f⁢(x)=L. (1.185)
Exemplo 1.4.6.

No Exemplo 1.4.3, vimos que

limx→∞x3−2⁢x+12−3⁢x3=−13. (1.186)

Logo, temos que y=−1/3 é uma assíntota horizontal do gráfico da função

f⁢(x)=x3−2⁢x+12−3⁢x3. (1.187)

Consulte a Figura 1.10.

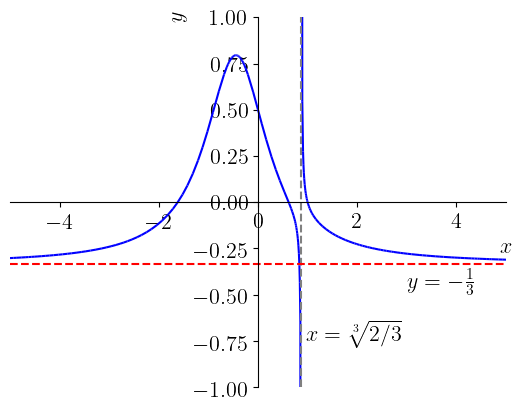
Refer to caption
Figura 1.10: Esboço do gráfico da função f⁢(x)=x3−2⁢x+12−3⁢x3.

Também, temos

limx→−∞x3−2⁢x+12−3⁢x3= limx→∞x3−3⁢x3 (1.188)
=−13. (1.189)

O que reforça que y=−1/3 é uma assíntota horizontal desta função.

Exemplo 1.4.7.

(Função exponencial natural)

limx→−∞ex=0, (1.190)

donde temos que y=0 é uma assíntota horizontal da função exponencial natural. Veja a Figura 1.11.

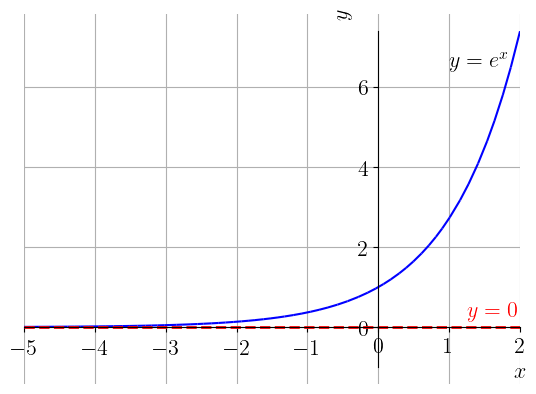
Refer to caption
Figura 1.11: Esboço do gráfico de f⁢(x)=ex.
Exemplo 1.4.8.

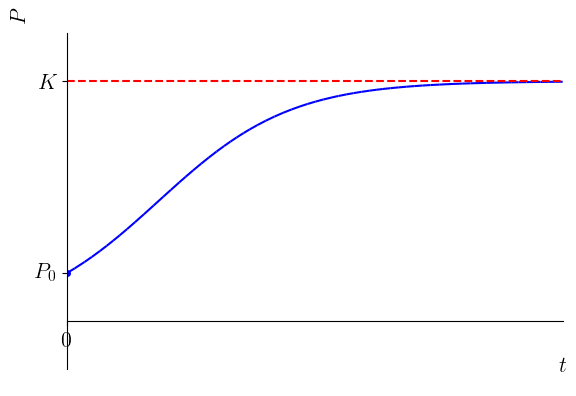
(Função logística) Na ecologia, a função logística 11endnote: 1Consulte mais em Wikipédia.

P⁢(t)=K1+(K−P0P0⁢e−r⁢t) (1.191)

é um modelo de crescimento populacional de espécies, sendo P⁢(t) o número de indivíduos da população no tempo t. O parâmetro P0 é o número de indíviduos na população no tempo inicial t=0, r>0 é a proporção de novos indivíduos na população devido a reprodução e K é o limite de saturação do crescimento populacional (devido aos recursos escassos como alimentos, território e tratamento a doenças). Observamos que

limt→∞P⁢(t)=limt→∞K1+(K−P0P0⁢e−r⁢t0)=K (1.192)

Ou seja, P⁢(t)=K é uma assíntota horizontal ao gráfico de P=P⁢(t) e é o limite de saturação do crecimento populacional. Na Figura 1.12, temos o esboço do gráfico da função logística para t≥0.

Refer to caption
Figura 1.12: Esboço do gráfico da função logistica.

1.4.2 Limite no infinito de função periódica

Uma função f é periódica quando existe um número T tal que

f⁢(x)=f⁢(x+T), (1.193)

para todo x∈ℝ no domínio de f. As funções trigonométricas são exemplos de funções periódicas22endnote: 2Consulte mais nas Notas de Aula - Pré-Cálculo - Funções Trigonométricas.

O limite no infinito de funções periódicas não existe33endnote: 3À exceção de funções constantes.. De fato, se f não é constante, então existem números x1≠x2 tal que y1=f⁢(x1)≠f⁢(x2)=y2. Como a função é periódica, f⁢(x1+k⁢T)=y1 e f⁢(x2+k⁢T)=y2 para todo número inteiro k. Desta forma, não existe número L que possamos tomar f⁢(x) arbitrariamente próxima, para todos os valores de x suficientemente grandes (ou pequenos).

Exemplo 1.4.9.

Não existe

limx→∞sen⁡(x), (1.194)

pois os valores de sen⁡x oscilam periodicamente no intervalo [−1,1]. Veja a Figura 1.13.

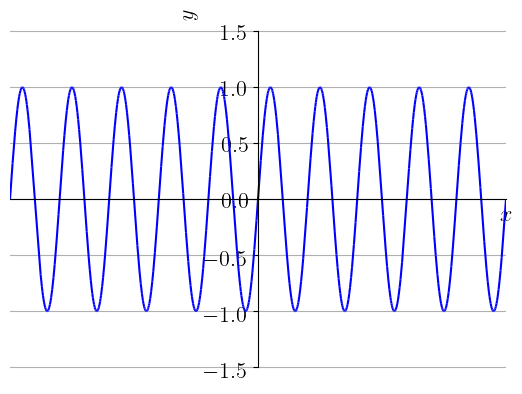
Refer to caption
Figura 1.13: Esboço do gráfico de f⁢(x)=sen⁡x.

Com o Python+SymPy, temos

Código 14: Python
⬇
1    >>> from sympy import *
2    >>> x = Symbol("x")
3    >>> limit(sin(x), x, oo)
4    AccumBounds(-1, 1)

indicando que o limite não existe, pois sen⁡x oscila indefinidamente no intervalo [−1,1].

1.4.3 Exercícios resolvidos

ER 1.4.1.

Calcule

limx→∞1x−1+1. (1.195)
Solução.

Utilizando a regra da soma para limites no infinito, temos

limx→∞1x−1+1 =limx→∞1x−1+limx→11 (1.196)
=limx→∞(1x−1)+1, (1.197)

observando que limx→∞1/(x−1) existe. De fato, o gráfico de g⁢(x)=1/(x−1) é uma translação de uma unidade à esquerda da função f⁢(x)=1/x. Uma translação horizontal finita não altera o comportamento da função para x→∞. Portanto, como f⁢(x)=1/x→∞ quando x→∞, temos que g⁢(x)=f⁢(x−1)=1/(x−1)→∞ quando x→∞, i.e.

limx→∞1x−1=0. (1.198)

Portanto, concluímos que

limx→∞1x−1+1=1. (1.199)

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

Código 15: Python
⬇
1    >>> from sympy import *
2    >>> x = Symbol("x")
3    >>> limit(1/(x-1)+1, x, oo)
4    1
ER 1.4.2.

Determine a(s) assíntota(s) horizontal(ais) do gráfico da função

f⁢(x)=3−x+4⁢x4−10⁢x3x2+2⁢x4−x. (1.200)
Solução.

Uma reta y=L é assíntota horizontal do gráfico de f, quando

limx→±∞f⁢(x)=L. (1.201)

Começamos com x→−∞, temos

limx→−∞f⁢(x) =limx→−∞3−x+4⁢x4−10⁢x3x2+2⁢x4−x (1.202)
=limx→−∞4⁢x42⁢x4=2. (1.203)

Logo, y=2 é assíntota horizontal ao gráfico de f⁢(x).

Agora, vamos ver a tendência da função para x→∞, temos

limx→∞f⁢(x) =limx→∞3−x+4⁢x4−10⁢x3x2+2⁢x4−x (1.204)
=42=2. (1.205)

Portanto, concluímos que y=2 é a única assíntota horizontal ao gráfico da função f.

Os seguintes comandos do Python+SymPy permitem plotar o esboço do gráfico da função f (linha azul) e sua assíntota horizontal (linha vermelha):

Código 16: Python
⬇
1    >>> from sympy import *
2    >>> x = Symbol("x")
3    >>> f = lambda x: (3-x+4*x**4-10*x**3)/(x**2+2*x**4-x)
4    >>> L = limit(f(x), x, oo)
5    >>> p = plot(f(x), (x, -15, 15), ylim = [-4, 6],\
6        line_color = "blue", show = False)
7    >>> q = plot(L, (x, -15, 15), line_color = "red", show = False)
8    >>> p.extend(q)
9    >>> p.show()
ER 1.4.3.

Calcule

limx→∞e−x. (1.206)
Solução.

Observamos que o gráfico de f⁢(x)=e−x é uma reflexão em torno do eixo y do gráfico da função g⁢(x)=ex. No Exemplo 1.4.7, vimos que

limx→−∞g⁢(x)=limx→−∞ex=0, (1.207)

logo

limx→∞e−x =limx→∞g⁢(−x) (1.208)
=limx→−∞g⁢(x)=0. (1.209)

Veja o esboço do gráfico de f⁢(x)=e−x na Figura 1.14.

Refer to caption
Figura 1.14: Esboço do gráfico de f⁢(x)=e−x.

Com o Python+SymPy, podemos computar este limite com o seguinte comando:

Código 17: Python
⬇
1    >>> from sympy import *
2    >>> x = Symbol("x")
3    >>> limit(exp(-x), x, oo)
4    0

1.4.4 Exercícios

E. 1.4.1.

Calcule

  1. a)

    limx→∞10x

  2. b)

    limx→−∞−10⁢x−1

  3. c)

    limx→−∞−10x2

  4. d)

    limx→∞1x−2

  5. e)

    limx→−∞2−(x+1)−1

Resposta.

a) 0; b) 0; c) 0; d) 0; e) 2;

E. 1.4.2.

Calcule

  1. a)

    limx→∞x−12

  2. b)

    limx→−∞1(x+1)3

  3. c)

    limx→∞x−s,s>0

Resposta.

a) 0; b) 0; c) 0

E. 1.4.3.

Calcule

  1. a)

    limx→−∞2x

  2. b)

    limx→∞(12)x+1

  3. c)

    limx→−∞2⋅3x+2

Resposta.

a) 0; b) 1; c) 2;

E. 1.4.4.

Calcule

  1. a)

    limx→−∞ex+1

  2. b)

    limx→∞3+e−x

  3. c)

    limx→∞2⁢e−x−1

  4. d)

    limx→−∞e−ex

Resposta.

a) 1; b) 3; c) −1; d) e

E. 1.4.5.

Calcule

  1. a)

    limx→∞1+x22⁢x

  2. b)

    limx→−∞1+x22⁢x

Resposta.

a) 12; b) −12

E. 1.4.6.

Calcule

limx→−∞cos⁡x. (1.210)
Resposta.

não existe.

E. 1.4.7.

Calcule:

  1. a)

    limx→∞1+e−x.

  2. b)

    limx→−∞1−2⁢xx+3−ex−1.

Resposta.

a) 1; b) −3

E. 1.4.8.

Dados dois polinômios p⁢(x)=an⁢xn+an−1⁢xn−1+⋯+a0 e q⁢(x)=bm⁢xm+bm−1⁢xm−1+⋯+b0, mostre que

limx→±∞p⁢(x)q⁢(x)=limx→±∞an⁢xnbm⁢xm. (1.211)
Resposta.

Dica: use as regras para o cálculo de limites.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |