Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

4 Integração 4 Integração 4.2 Propriedades de integração

4.1 Noção de integral

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.1.1 Soma de Riemann

Seja $f$ uma função contínua definida em um intervalo fechado $[a,b]$ . Seja, também, $P$ a seguinte partição de $[a,b]$

P=\{a=x_{0}<x_{1}<x_{2}<\cdots<x_{n}=b\},

(4.1)

onde $n+1$ é o número de pontos na partição. Definimos

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\Delta x_{i}=x% _{i}-x_{i-1}

(4.2)

o tamanho de cada subintervalo $I_{i}=[x_{i-1},x_{i}]$ da partição, com $i=1,2,\cdots,n$ . A norma da partição é definida por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\|P\|:=\max_{i% =1,\dotsc,n}\Delta x_{i},

(4.3)

i.e. o tamanho do maior subintervalo da partição. Com isso, chama-se de uma soma de Riemann³⁵³⁵endnote: ³⁵Georg Friedrich Bernhard Riemann, 1826 - 1866, matemático alemão. Fonte: Wikipédia: Bernhard Riemann. toda a expressão da forma

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}S_{n}:=\sum_{i% =1}^{n}f(x_{i}^{*})\Delta x_{i},

(4.4)

onde $x_{i}^{*}\in[x_{i},x_{i-1}]$ (arbitrariamente escolhido). Consulte a Figura 4.1.

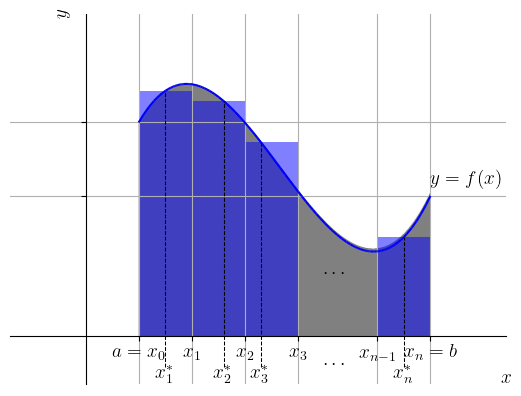
Refer to caption — Figura 4.1: Ilustração da soma de Riemann.

No caso de uma função não negativa, uma soma de Riemann é uma aproximação da área sob seu gráfico e o eixo das abscissas³⁶³⁶endnote: ³⁶Consulte o Exercício 4.1.4 para uma interpretação geométrica no caso geral de funções contínuas..

4.1.2 Integral

A integral (definida) de $a$ até $b$ de uma dada função $f$ em relação a $x$ é denotada e definida por

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\int_{a}^{b}f(% x)\,dx:=\lim_{\|P\|\to 0}\sum_{i=1}^{n}f(x_{i}^{*})\Delta x_{i}.

(4.5)

De forma genérica, a integral definida de $a$ até $b$ é o limite das somas de Riemann quando a norma das partições $P$ do intervalo $[a,b]$ tendem a zero. Quando o limite existe, dizemos que $f$ é integrável no intervalo $[a,b]$ .

Na notação de integral definida acima, chamamos $a$ de limite inferior e $b$ de limite superior de integração, $f$ é chamada de integrando e $x$ de variável de integração.

Observação 4.1.1.

Funções contínuas são funções integráveis.

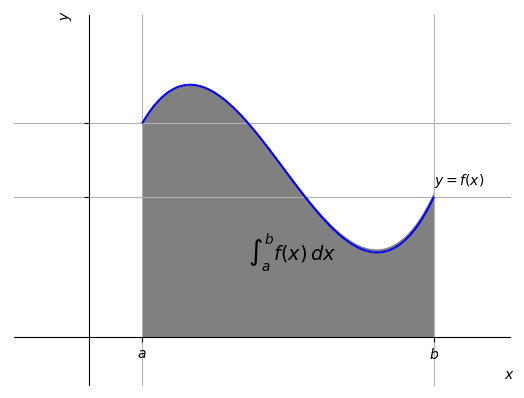
Observação 4.1.2.

(Área sob o gráfico) No caso de uma função não negativa,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\int_{a}^{b}f(% x)\,dx

(4.6)

é a área sob o gráfico de $f$ ³⁷³⁷endnote: ³⁷Consulte o Exercício 4.1.5 para uma interpretação geométrica no caso geral de funções contínuas.. Consulte a Figura 4.2.

Exemplo 4.1.1.

Vamos calcular

\int_{0}^{1}1\,dx.

(4.7)

Aqui, o integrando é a função constante $f(x)\equiv 1$ e o intervalo de integração é $[a,b]$ . Da Observação 4.1.2, temos que esta integral é a área sob o gráfico de $f$ no intervalo $[0,1]$ . Esta área é um retângulo de altura $1$ e comprimento $1$ . Logo,

\int_{0}^{1}1\,dx=1\cdot 1=1.

(4.8)

Com o Python+SymPy, podemos computar esta integral com os seguintes comandos

Código 62: Python

⬇

1 >>> from sympy import *

2 >>> x = Symbol('x')

3 >>> integrate(1, (x,0,1))

4 1

4.1.3 Exercícios resolvidos

ER 4.1.1.

Calcule

\int_{-1}^{1}\sqrt{1-x^{2}}\,dx.

(4.9)

Solução.

Esta integral corresponde à área sob o gráfico da função $f(x)=\sqrt{1-x^{2}}$ restrita ao intervalo $[-1,1]$ . Observando que

	$\displaystyle y=\sqrt{x^{2}-1}$	$\displaystyle\Rightarrow y^{2}=1-x^{2}$		(4.10)
		$\displaystyle\Rightarrow y^{2}+x^{2}=1,$		(4.11)

vemos que esta é a área do semicírculo de raio $1$ . Logo,

\int_{-1}^{1}\sqrt{1-x^{2}}\,dx=\frac{\pi\cdot 1^{2}}{2}=\frac{\pi}{2}.

(4.12)

Com o Python+SymPy, podemos computar esta integral com os seguintes comandos

Código 63: Python

⬇

1 In : from sympy import *

2 >>> x = Symbol('x')

3 >>> integrate(sqrt(1-x**2), (x,-1,1))

4 pi/2

ER 4.1.2.

Determine a função $F(x)$ tal que

F(x)=\int_{0}^{x}t\,dt,

(4.13)

para todo $x\geq 0$ . Então, mostre que $F^{\prime}(x)=x$ .

Solução.

A integral definida

\int_{0}^{x}t\,dt

(4.14)

é a área sob o gráfico de $f(t)=t$ restrita no intervalo $[0,x]$ . Isto é, a área do triângulo retângulo de base $x$ e altura $x$ . Logo,

F(x)=\int_{0}^{x}t\,dt=\frac{x\cdot x}{2}=\frac{x^{2}}{2}.

(4.15)

Ou seja, temos $F(x)=x^{2}/2$ e, portanto,

F^{\prime}(x)=\frac{1}{2}\cdot 2x=x.

(4.16)

Com o Python+SymPy, podemos fazer essas computações com os seguintes comandos

Código 64: Python

⬇

1 In : from sympy import *

2 >>> x, t = symbols('x,t')

3 >>> F = integrate(t, (t,0,x))

4 >>> print("F(x) = ", F)

5 >>>

6 F(x) = x**2/2

7 In : diff(F,x)

8 x

4.1.4 Exercícios

E. 4.1.1.

Calcule

\int_{-1}^{2}2\,dx.

(4.17)

Resposta.

$6$

E. 4.1.2.

Calcule

\int_{-3}^{-1}1-x\,dx.

(4.18)

Resposta.

$6$

E. 4.1.3.

Determine $F(x)$ tal que

F(x)=\int_{0}^{x}t+1\,dt.

(4.19)

para $x\geq 0$ . Então, calcule $F^{\prime}(x)$ .

Resposta.

$\displaystyle F(x)=\frac{x^{2}}{2}+x$ ; $F^{\prime}(x)=x+1$ .

E. 4.1.4.

Faça uma interpretação geométrica da uma soma de Riemann aplicada a uma função contínua e não positiva. Estenda sua interpretação para funções contínuas arbitrárias.

Resposta.

Dica: a soma de Riemann é uma aproximação da área líquida sob o gráfico da função.

E. 4.1.5.

Faça uma interpretação geométrica de

\int_{a}^{b}f(x)\,dx

(4.20)

quando $f$ é uma função contínua e não positiva. Estenda sua interpretação para funções contínuas arbitrárias.

Resposta.

Dica: $\displaystyle\int_{a}^{b}f(x)\,dx$ é a área líquida sob o gráfico da função.

E. 4.1.6.

Calcule

\int_{-1}^{2}-1\,dx.

(4.21)

Resposta.

$-3$

E. 4.1.7.

Calcule

\int_{-1}^{1}x\,dx.

(4.22)

Resposta.

$0$

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |