Matemática Numérica II

6 Equações Diferenciais Parciais 6.2 Equação do Calor Referências

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

6.3 Equação da Onda

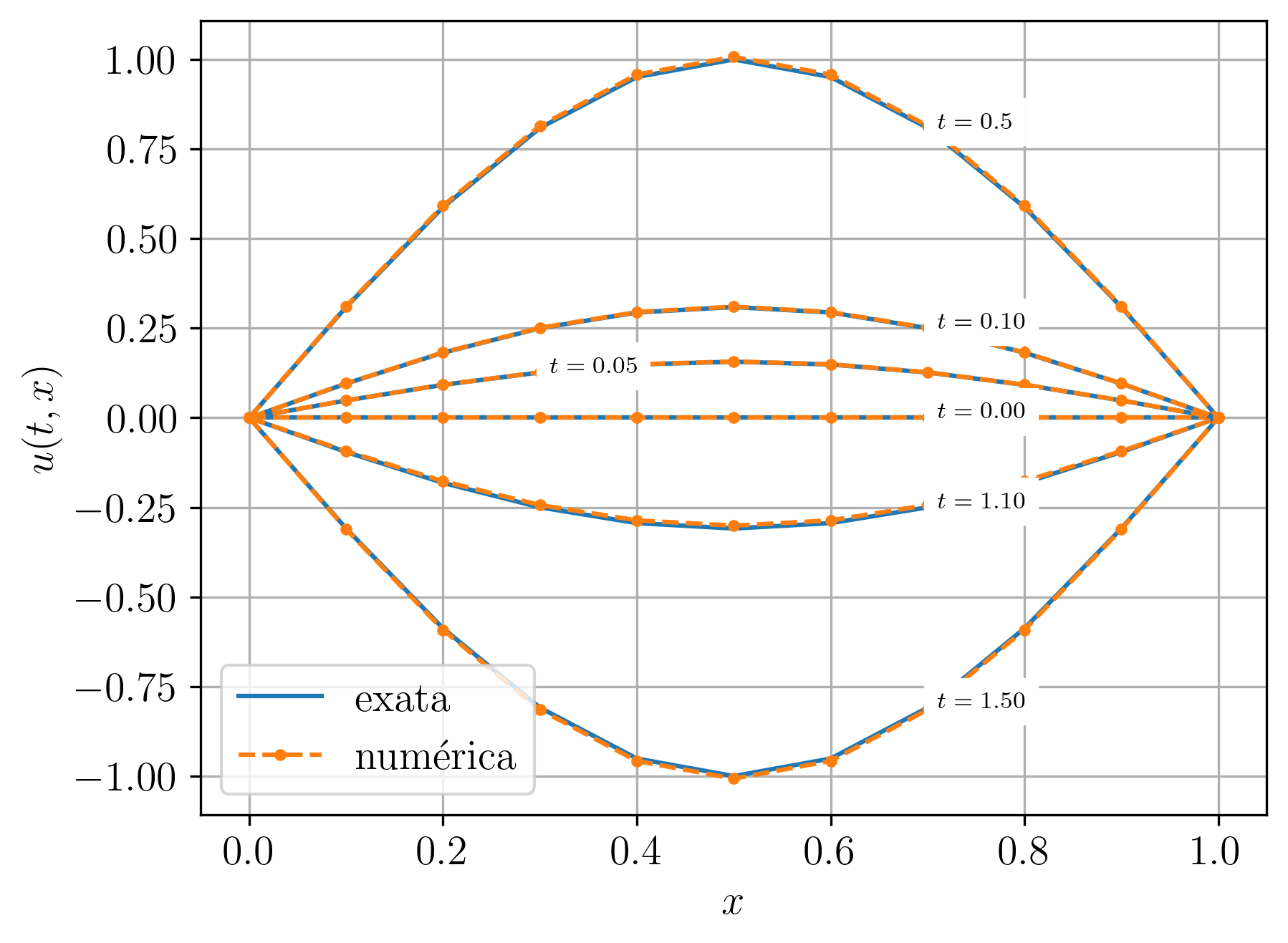
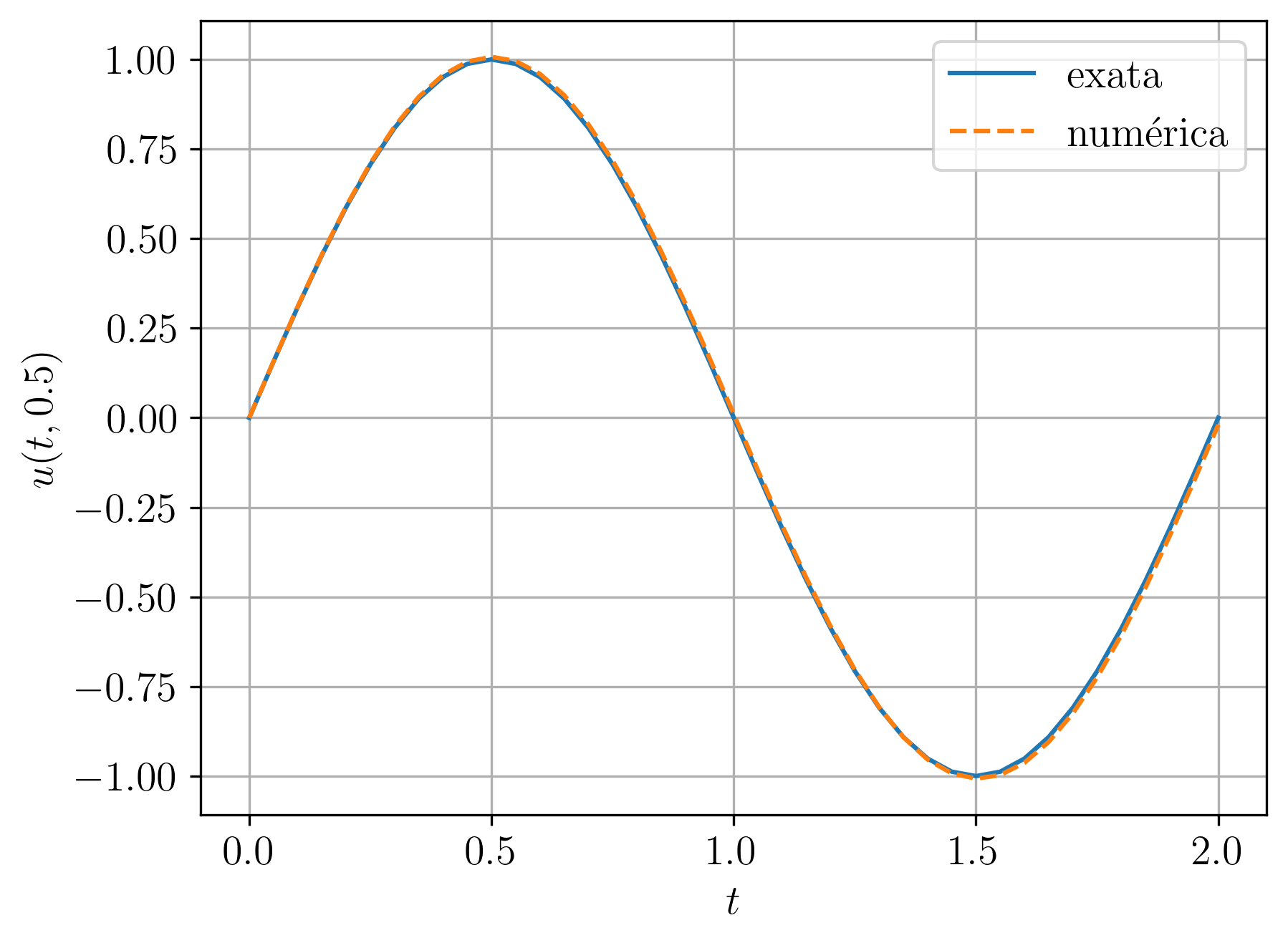
Consideramos a equação da onda com condições iniciais dadas e condições de contorno de Dirichlet homogêneas


	$\displaystyle u_{tt}-\alpha u_{xx}=0,\leavevmode\nobreak\ 0<t\leq t_{f},% \leavevmode\nobreak\ a<x<b,$		(6.39a)
	$\displaystyle u(0,x)=f(x),\leavevmode\nobreak\ a\leq x\leq b,$		(6.39b)
	$\displaystyle u_{t}(0,x)=g(x),\leavevmode\nobreak\ a\leq x\leq b,$		(6.39c)
	$\displaystyle u(t,a)=u(t,b)=0,\leavevmode\nobreak\ 0\leq t\leq t_{f},$		(6.39d)

onde $u=u(t,x)$ é a incógnita com $f$ , $g$ e $\alpha>0$ dadas.

Para a aplicação do Método das Diferenças Finitas (MDF), assumimos as discretizações: no tempo, $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}t^{(k)}=kh_{t}$ , $j=0,1,\dotsc,n_{t}$ , $h_{t}=t_{f}/n_{t}$ ; no espaço $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{i}=a+(i-1)% h_{x}$ , $i=1,2,\dotsc,n_{x}+1$ , $h_{x}=(b-a)/n_{x}$ . Então, assumindo a notação $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}u^{(k)}_{i}% \approx u\left(t^{(k)},x_{i}\right)$ usando a fórmula de diferenças finitas central $D^{2}_{0,h^{2}}$ , obtemos a seguinte forma discreta da equação Eq. (6.39a)

		$\displaystyle\frac{u^{(k-1)}_{i}-2u^{(k)}_{i}+\color[rgb]{0,0,1}\definecolor[% named]{pgfstrokecolor}{rgb}{0,0,1}u^{(k+1)}_{i}}{h_{t}^{2}}$		(6.40)
		$\displaystyle\quad-\alpha\frac{u^{(k)}_{i}-2u^{(k)}_{i}+u^{(k)}_{i+1}}{h_{x}^{% 2}}=0,$		(6.40)

para $i=2,3,\dotsc,n_{x}$ , $j=1,2,\dotsc,n_{t}-1$ . Denotando $\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\lambda:=% \alpha h_{t}^{2}/h_{x}^{2}$ , rearranjando os termos e aplicando as condições de contorno, obtemos


	$\displaystyle u^{(k+1)}_{2}=2\left(1-\lambda\right)u^{(k)}_{2}+\lambda u^{(k)}% _{3}-u^{(k-1)}_{2},$		(6.41a)
	$\displaystyle u^{(k+1)}_{i}=\lambda u^{(k)}_{i}+2(1-\lambda)u^{(k)}_{i}+% \lambda u^{(k)}_{i+1}-u^{(k-1)}_{i},$		(6.41b)
	$\displaystyle u^{(k+1)}_{n_{x}}=\lambda u^{(k)}_{n_{x}-1}+2(1-\lambda)u^{(k)}_% {n_{x}}-u^{(k-1)}_{n_{x}},$		(6.41c)

para $i=2,3,\dotsc,n_{x}$ , $j=1,2,\dotsc,n_{t}-1$ . Ou, equivalentemente, na forma matricial

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\tilde{% \boldsymbol{u}}^{(k+1)}=A\tilde{\boldsymbol{u}}^{(k)}-\tilde{\boldsymbol{u}}^{% (k-1)},

(6.42)

para $k=1,2,\dotsc,n_{t}-1$ , onde $\tilde{\boldsymbol{u}}^{(k)}=\left(u^{(k)}_{i}\right)_{i=2}^{n_{x}}$ e $A=[a_{i,j}]_{i,j=1}^{n_{x}-1,n_{x}-1}$ é a matriz tridiagonal de elementos

a_{i,j}=\left\{\begin{array}[]{ll}a_{i,i-1}=\lambda&,1<i\leq n_{x}-1,\\ a_{i,i}=2(1-\lambda)&,1\leq i\leq n_{x}-1,\\ a_{i,i+1}=\lambda&,1\leq i<n_{x}-1.\\ \end{array}\right.

(6.43)

Para a inicialização, a Eq. (6.42) requer que conhecemos $\tilde{\boldsymbol{u}}^{(0)}$ e $\tilde{\boldsymbol{u}}^{(1)}$ . A primeira, vem diretamente da condição inicial Eq. (6.39b), i.e.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\tilde{% \boldsymbol{u}}^{(0)}=f\left(\tilde{\boldsymbol{x}}\right),

(6.44)

onde $\tilde{\boldsymbol{x}}=\left(x_{i}\right)_{i=2}^{n_{x}}$ . Agora, aplicando a fórmula de diferenças finitas progressiva $D_{+,h}$ , temos da condição inicial Eq. (6.39c)

\frac{\tilde{\boldsymbol{u}}^{(1)}-\tilde{\boldsymbol{u}}^{(0)}}{h_{t}}=g\left% (\tilde{\boldsymbol{x}}\right)

(6.45)

ou, equivalentemente,

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\tilde{% \boldsymbol{u}}^{(1)}=\tilde{\boldsymbol{u}}^{(0)}+h_{t}g\left(\tilde{% \boldsymbol{x}}\right).

(6.46)

De tudo isso, temos que a solução numérica da equação da onda pode ser computada com a seguinte iteração


	$\displaystyle\tilde{\boldsymbol{u}}^{(0)}=f\left(\tilde{\boldsymbol{x}}\right),$		(6.47a)
	$\displaystyle\tilde{\boldsymbol{u}}^{(1)}=\tilde{\boldsymbol{u}}^{(0)}+h_{t}g% \left(\tilde{\boldsymbol{x}}\right),$		(6.47b)
	$\displaystyle\tilde{\boldsymbol{u}}^{(k+1)}=A\tilde{\boldsymbol{u}}^{(k)}-% \tilde{\boldsymbol{u}}^{(k-1)},$		(6.47c)

para $k=1,2,\dotsc,n_{t}-1$ , com $\boldsymbol{u}^{(k)}=\left(0,\tilde{\boldsymbol{u}},0\right)$ .

Observação 6.3.1.

(Condição de Estabilidade e Erro de Truncamento.) Pode-se mostrar a seguinte condição de estabilidade [3, p. 487]

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\alpha\frac{h% _{t}}{h_{x}}\leq 1.

(6.48)

Com isso e para $f$ e $g$ suficientemente suaves, o esquema numérica (6.47) tem erro de truncamento $O(h_{t}^{2}+h_{x}^{2})$ .

Exemplo 6.3.1.

Consideramos o seguinte problema


	$\displaystyle u_{tt}-u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 2,\leavevmode% \nobreak\ 0<x<1,$		(6.49a)
	$\displaystyle u(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.49b)
	$\displaystyle u_{t}(0,x)=\pi\operatorname{sen}(\pi x),\leavevmode\nobreak\ 0% \leq x\leq 1,$		(6.49c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 2.$		(6.49d)

Sua solução exata é $u(t,x)=\operatorname{sen}(\pi t)\operatorname{sen}(\pi x)$ . A Figura 6.6 contém gráficos de comparação entra as soluções numérica e exata. Para a solução numérica, tomamos $n_{t}=40$ ( $h_{t}=0.05$ ) e $n_{x}=10$ ( $h_{x}=0.1$ ).

Refer to caption — Figura 6.6: Gráficos comparativos das soluções numérica e exata do problema de onda do Exemplo 6.3.1.

⬇

1import numpy as np

2from numpy import pi, sin, cos

4# params

5nt = 40

6ht = 2./nt

7tt = np.linspace(0., 2., nt+1)

9nx = 10

10hx = 1./nx

11xx = np.linspace(0., 1., nx+1)

13# c.i.s

14def f(x):

15 return np.zeros_like(x)

17def g(x):

18 return pi*sin(pi*x)

20# axiliares

21lbda = ht**2/hx**2

23A = np.zeros(((nx-1), (nx-1)))

24A[0,0] = 2*(1. - lbda)

25A[0,1] = lbda

26for i in range(1,nx-2):

27 A[i,i-1] = lbda

28 A[i,i] = 2*(1 - lbda)

29 A[i,i+1] = lbda

30A[nx-2,nx-3] = lbda

31A[nx-2,nx-2] = 2*(1 - lbda)

33# laço no tempo

34## c.i.s

35u0 = f(xx)

37u1 = u0.copy()

38u1[1:-1] = u0[1:-1] + ht*g(xx[1:-1])

40u = u1.copy()

41for k in range(1,nt):

43 print(f'{k+1}: t = {tt[k+1]:f}')

45 u[1:-1] = A@u1[1:-1] - u0[1:-1]

47 u0 = u1.copy()

48 u1 = u.copy()

6.3.1 Exercício

E. 6.3.1.

Considere o problema


	$\displaystyle u_{tt}-u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 1.5,\leavevmode% \nobreak\ 0<x<1,$		(6.50a)
	$\displaystyle u(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.50b)
	$\displaystyle u_{t}(0,x)=\pi\operatorname{sen}(\pi x),\leavevmode\nobreak\ 0% \leq x\leq 1,$		(6.50c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 1.5.$		(6.50d)

Sua solução exata é $u(t,x)=\operatorname{sen}(\pi t)\operatorname{sen}(\pi x)$ . Faça testes numéricos para determinar os passos $h_{t}$ e $h_{x}$ para os quais o esquema numérico (6.47) compute o valor de $u(1.5,0.5)$ com $5$ dígitos significativos corretos.

$h_{t}=2.5\mathrm{e}\!-3\!$ , $h_{x}=1.\mathrm{e}\!-2\!$

E. 6.3.2.

Considere o problema


	$\displaystyle u_{tt}-u_{xx}=e^{-t}(2+x-x^{2}),\leavevmode\nobreak\ 0<t\leq 1,% \leavevmode\nobreak\ 0<x<1,$		(6.51a)
	$\displaystyle u(0,x)=x-x^{2},\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.51b)
	$\displaystyle u_{t}(0,x)=x^{2}-x,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.51c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 1.$		(6.51d)

Sua solução exata é $u(t,x)=e^{-t}(x-x^{2})$ . Implemente um esquema numérico semelhante ao (6.47) para computar soluções numéricas desse problema.

E. 6.3.3.

Considere o problema


	$\displaystyle u_{tt}-u_{xx}=e^{-t}(2+x-x^{2}),\leavevmode\nobreak\ 0<t\leq 1,% \leavevmode\nobreak\ 0<x<1,$		(6.52a)
	$\displaystyle u(0,x)=x-x^{2},\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.52b)
	$\displaystyle u_{t}(0,x)=x^{2}-x,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.52c)
	$\displaystyle u_{x}(t,0)=e^{-t},\leavevmode\nobreak\ 0\leq t\leq 1,$		(6.52d)
	$\displaystyle u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 1.$		(6.52e)

Sua solução exata é $u(t,x)=e^{-t}(x-x^{2})$ . Implemente um esquema numérico semelhante ao (6.47) para computar soluções numéricas desse problema.

E. 6.3.4.

Considere o problema


	$\displaystyle u_{tt}-u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 2,\leavevmode% \nobreak\ 0<x<1,$		(6.53a)
	$\displaystyle u(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.53b)
	$\displaystyle u_{t}(0,x)=\pi\operatorname{sen}(\pi x),\leavevmode\nobreak\ 0% \leq x\leq 1,$		(6.53c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 2.$		(6.53d)

Sua solução exata é $u(t,x)=\operatorname{sen}(\pi t)\operatorname{sen}(\pi x)$ . Baseado em (6.47), desenvolva um novo esquema numérico substituindo o passo (6.47b) por um esquema numérico de mais alta ordem.

Dica: use, por exemplo, um método de R-K-2.

E. 6.3.5.

Considere o problema


	$\displaystyle u_{tt}-\alpha u_{xx}=0,\leavevmode\nobreak\ 0<t\leq 1,% \leavevmode\nobreak\ 0<x<1,$		(6.54a)
	$\displaystyle u(0,x)=x(1-x),\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.54b)
	$\displaystyle u_{t}(0,x)=0,\leavevmode\nobreak\ 0\leq x\leq 1,$		(6.54c)
	$\displaystyle u(t,0)=u(t,1)=0,\leavevmode\nobreak\ 0\leq t\leq 2.$		(6.54d)

Use o esquema numérico (6.47) para fazer testes numéricos para $\alpha=1.,0.5,0.1,0.01$ . É necessário ajustar os parâmetros $h_{t}$ e $h_{x}$ ao variar o parâmetro $\alpha$ ? Justifique sua resposta.

Dica: consulte a Observação 6.3.1.

Notas

1 Para fixar notação, assumiremos $h>0$ ao longo deste capítulo.
2 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
3 Consulte [3, Cap. 7,Sec. 1.1], para uma abordagem mais geral.
4 Neste capítulo, $h$ é escolhido como a distância entre os nodos.
5 Thomas Simpson, 1710 - 1761, matemático britânico. Fonte: Wikipédia: Thomas Simpson.
6 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
7 Para a estimativa do erro de truncamento, consulte o Exercício 3.1.5.
8 Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.
9 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
10 Equações Diferenciais Ordinárias
11 Brook Taylor, 1685 - 1731, matemático britânico. Fonte: Wikipédia:Brook Taylor.
12 Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.
13 Carl David Tolmé Runge, 1856 - 1927, matemático alemão. Fonte: Wikipédia: Carl Runge.
14 Martin Wilhelm Kutta, 1867 - 1944, matemático alemão. Fonte: Wikipédia: Martin Wilhelm Kutta.
15 Consulte (4.84) para mais detalhes sobre a expansão em polinômio de Taylor de $\Delta(t,y;h)$ .
16 Leonhard Paul Euler, 1707-1783, matemático e físico suíço. Fonte: Wikipédia: Ronald Fisher.
17 Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.
18 Roger Cotes, 1682 - 1716, matemático inglês. Fonte: Wikipédia: Roger Cotes.
19 Consulte as Notas de Aula: Matemática Numérica II: Integração: Regras de Newton-Cotes.
20 Consulte o Exercício 4.5.6
21 Com erro de truncamento local de $O(h^{2})$ .
22 Por convenção, (5.2a)-(5.2c) é chamado de formulação forte do problema.
23 $u\in L^{2}([a,b])\Leftrightarrow\int_{a}^{b}|u|^{2}\,dx<\infty$ .
24 $H_{0}^{1}([a,b]):=\{u=u(x);\leavevmode\nobreak\ u,u^{\prime}\in L^{2}([a,b]),u% (a)=u(b)=0\}$ .
25 Por simplicidade, usando a regra do ponto médio para aproximar as integrais.
26 Isaac Newton, 1642 - 1727, matemático, físico, astrônomo, teólogo e autor inglês. Fonte: Wikipédia: Isaac Newton.
27 Carl Gustav Jakob Jacobi, 1804 - 1851, matemático alemão. Fonte: Wikipédia: Carl Gustav Jakob Jacobi.
28 Siméon Denis Poisson, 1781 - 1840, matemático francês. Fonte: Wikipédia:Siméon Denis Poisson.
29 Pierre-Simon Laplace, 1749 - 1827, matemático francês. Fonte: Wikipédia: Pierre-Simon Laplace.
30 Carl Gottfried Neumann, 1832 - 1925, matemático alemão. Fonte: Wikipédia: Carl Neumann.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Matemática Numérica II

6.3 Equação da Onda

Observação 6.3.1.

Exemplo 6.3.1.

6.3.1 Exercício

E. 6.3.1.

E. 6.3.2.

E. 6.3.3.

E. 6.3.4.

E. 6.3.5.

Envie seu comentário