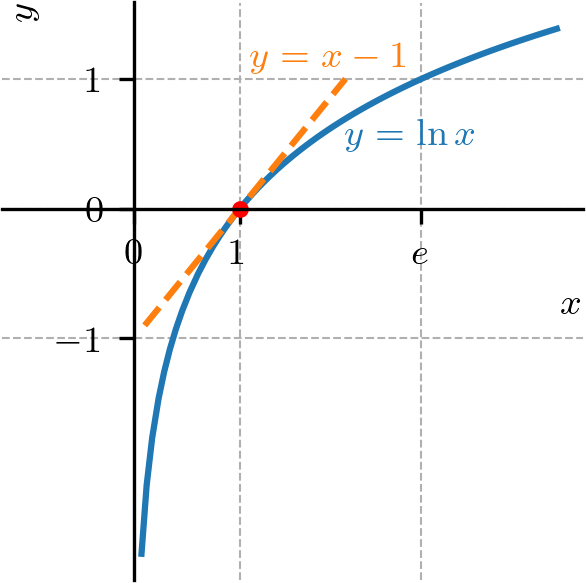Cálculo I

3 Derivadas 3.8 Regra da cadeia 3.10 Derivação implícita

Material disponível para compra: apostila. Consulte outras formas de colaboração aqui!

3.9 Diferenciabilidade da função inversa

Seja $f$ uma função diferenciável e injetora em um intervalo aberto $I$ . Então, pode-se mostrar que sua inversa $f^{-1}$ é diferenciável em qualquer ponto da imagem da $f$ no qual $f^{\prime}(f^{-1}(x))\neq 0$ e sua derivada é

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\frac{d}{dx}% [f^{-1}(x)]=\frac{1}{f^{\prime}(f^{-1}(x))}}.

(3.527)

De fato, temos

f\left(f^{-1}(x)\right)=x.

(3.528)

Derivando ambos os lados desta equação em relação a $x$ e usando a regra da cadeia, obtemos

	$\displaystyle\frac{d}{dx}\left[f\left(f^{-1}(x)\right)\right]=\frac{d}{dx}(x)$		(3.529)
	$\displaystyle f^{\prime}\left(f^{-1}(x)\right)\cdot\frac{d}{dx}\left[f^{-1}(x)% \right]=1$		(3.530)
	$\displaystyle\frac{d}{dx}\left[f^{-1}(x)\right]=\frac{1}{f^{\prime}\left(f^{-1% }(x)\right)}.$		(3.531)

Exemplo 3.9.1.

Seja $f(x)=(2x-1)^{2}$ para $x>1/2$ . Para calcular sua inversa, fazemos

	$\displaystyle y=(2x-1)^{2}$		(3.532)
	$\displaystyle\sqrt{y}=2x-1$		(3.533)
	$\displaystyle x=\frac{\sqrt{y}+1}{2}$		(3.534)

Ou seja,

f^{-1}(x)=\frac{1}{2}(\sqrt{x}+1).

(3.535)

Calculando a derivada de $f^{-1}$ diretamente, temos

	$\displaystyle\frac{d}{dx}f^{-1}(x)=\frac{1}{2}\left(\sqrt{x}+1\right)^{\prime}$		(3.536)
	$\displaystyle\text{}\quad=\frac{1}{2}\cdot\frac{1}{2\sqrt{x}}$		(3.537)
	$\displaystyle\text{}\quad=\frac{1}{4\sqrt{x}}$		(3.538)

Agora, usando (3.527) e observando que $f^{\prime}(x)=8x-4$ , obtemos

	$\displaystyle\frac{d}{dx}f^{-1}(x)=\frac{1}{f^{\prime}(f^{-1}(x))},$		(3.539)
	$\displaystyle\text{}\quad=\frac{1}{8\cdot\frac{1}{2}\left(\sqrt{x}+1\right)-4},$		(3.540)
	$\displaystyle\text{}\quad=\frac{1}{4\sqrt{x}},$		(3.541)

como esperado.

Observação 3.9.1.(Derivada da função logarítmica)

A derivada da função logarítmica pode ser obtida usando (3.527).

•

Tomando $f(x)=e^{x}$ temos $f^{-1}(x)=\ln x$ e, daí por (3.527)

$\frac{d}{dx}\ln x=\frac{1}{e^{\ln x}}=\frac{1}{x}.$ (3.542)
•

Tomando $f(x)=a^{x}$ , $a>0$ e $a\neq 1$ , temos $f^{-1}(x)=\log_{a}x$ e, por (3.527),

$\frac{d}{dx}\log_{a}x=\frac{1}{a^{\log_{a}x}\ln a}=\frac{1}{x\ln a}.$ (3.543)

Exemplo 3.9.2.

Vamos calcular a derivada em relação a $x$ da função

f(x)=\ln\frac{1}{x}.

(3.544)

Aplicando a regra da cadeia na derivada da função logarítmica, temos

\frac{d}{dx}\ln u=\frac{1}{u}\frac{du}{dx}.

(3.545)

Portanto, temos

	$\displaystyle f^{\prime}(x)=\left(\ln\frac{1}{x}\right)^{\prime}$		(3.546)
	$\displaystyle\text{}\quad=\frac{1}{x^{-1}}\cdot(-x^{-2})$		(3.547)
	$\displaystyle\text{}\quad=-\frac{1}{x}.$		(3.548)

Código 71: Python

⬇

1from sympy import log, diff

2from sympy.abc import x

3diff(log(1/x), x)

-1/x

3.9.1 Derivadas de funções trigonométricas inversas

Seja $f(x)=\operatorname{sen}x$ restrita a $-\pi/2\leq x\leq\pi/2$ . Sua inversa é a função arco seno, denotada por

y=\operatorname{arc}\operatorname{sen}x.

(3.549)

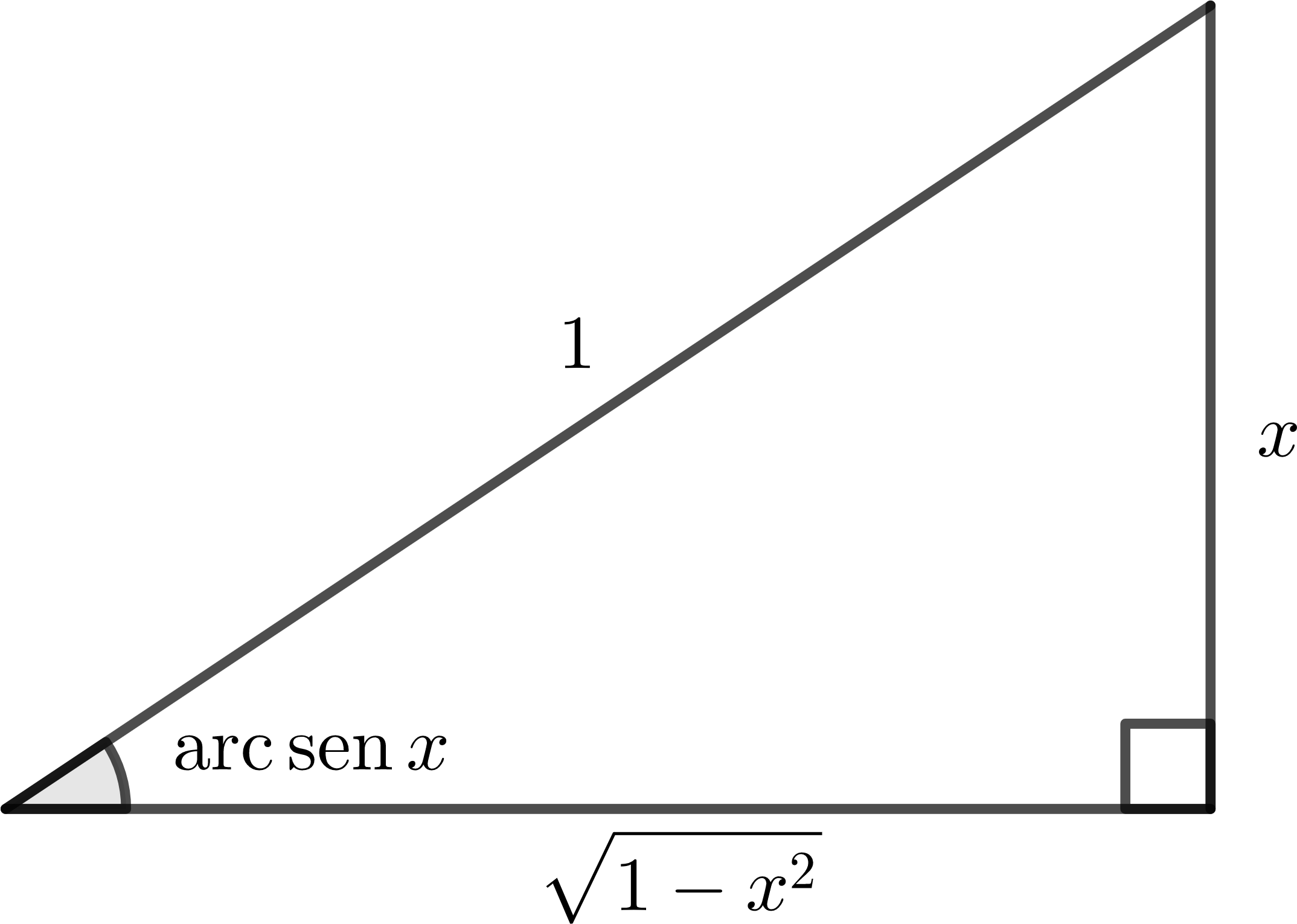
Refer to caption — Figura 3.11: Arco seno de um ângulo no triângulo retângulo.

Para calcular a derivada da função arco seno, vamos usar (3.527) com $f(x)=\operatorname{sen}x$ e $f^{\prime}(x)=\operatorname{arc}\operatorname{sen}x$ , donde

(\operatorname{arc}\operatorname{sen}x)^{\prime}=\frac{1}{\cos(\operatorname{% arc}\operatorname{sen}x)}.

(3.550)

Como $\cos(\operatorname{arc}\operatorname{sen}x)=\sqrt{1-x^{2}}$ (consultemos a Figura 3.11), concluímos

(\operatorname{arc}\operatorname{sen}x)^{\prime}=\frac{1}{\sqrt{1-x^{2}}}.

(3.551)

Exemplo 3.9.3.

A regra da cadeia aplicada à derivada da função arco seno é

\frac{d}{dx}\operatorname{arc}\operatorname{sen}u=\frac{1}{\sqrt{1-u^{2}}}% \frac{du}{dx}.

(3.552)

Por exemplo, temos

\frac{d}{dx}\operatorname{arc}\operatorname{sen}x^{2}=\frac{2x}{\sqrt{1-x^{4}}}.

(3.553)

Código 72: Python

⬇

1from sympy import diff, asin

2from sympy.abc import x

3diff(asin(x**2), x)

2*x/sqrt(1 - x**4)

Com argumentos análogos aos usados no cálculo da derivada da função arco seno, podemos obter as seguintes derivadas:

	$\displaystyle(\operatorname{arc}\cos x)^{\prime}=-\frac{1}{\sqrt{1-x^{2}}}$		(3.554)
	$\displaystyle(\operatorname{arc}\operatorname{tg}x)^{\prime}=\frac{1}{1+x^{2}}$		(3.555)
	$\displaystyle(\operatorname{arc}\operatorname{cotg}x)^{\prime}=-\frac{1}{1+x^{% 2}}$		(3.556)
	$\displaystyle(\operatorname{arc}\sec x)^{\prime}=\frac{1}{\|x\|\sqrt{x^{2}-1}}$		(3.557)
	$\displaystyle(\operatorname{arc}\operatorname{cossec}x)^{\prime}=-\frac{1}{\|x\|% \sqrt{x^{2}-1}}$		(3.558)

Exemplo 3.9.4.

A regra da cadeia aplicada a função arco tangente é

\frac{d}{dx}\operatorname{arc}\operatorname{tg}u=\frac{1}{1+u^{2}}\frac{du}{dx}.

(3.559)

Por exemplo, temos

	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{tg}\sqrt{x}=\frac{1}{% 1+(\sqrt{x})^{2}}\frac{d}{dx}\sqrt{x}$		(3.560)
	$\displaystyle\text{}\quad=\frac{1}{2(1+x)\sqrt{x}}.$		(3.561)

Código 73: Python

⬇

1from sympy import diff, atan, sqrt

2from sympy.abc import x

3diff(atan(sqrt(x)), x)

1/(2*sqrt(x)*(x + 1))

3.9.2 Lista de derivadas

	$\displaystyle(ku)^{\prime}=ku^{\prime}$		(3.562)
	$\displaystyle(u\pm v)^{\prime}=u^{\prime}\pm v^{\prime}$		(3.563)
	$\displaystyle(uv)^{\prime}=u^{\prime}v+uv^{\prime}$		(3.564)
	$\displaystyle\left(\frac{u}{v}\right)^{\prime}=\frac{u^{\prime}v-uv^{\prime}}{% v^{2}}$		(3.565)
	$\displaystyle(k)^{\prime}=0$		(3.566)
	$\displaystyle(x)^{\prime}=1$		(3.567)
	$\displaystyle\frac{d}{dx}u^{r}=ru^{r-1}\frac{du}{dx}$		(3.568)
	$\displaystyle\frac{d}{dx}a^{u}=a^{u}\ln a\frac{du}{dx}$		(3.569)
	$\displaystyle\frac{d}{dx}e^{u}=e^{u}\frac{du}{dx}$		(3.570)
	$\displaystyle\frac{d}{dx}\log_{a}u=\frac{1}{u\ln a}\frac{du}{dx}$		(3.571)
	$\displaystyle\frac{d}{dx}\ln u=\frac{1}{u}\frac{du}{dx}$		(3.572)
	$\displaystyle\frac{d}{dx}\operatorname{sen}u=\cos(u)\frac{du}{dx}$		(3.573)
	$\displaystyle\frac{d}{dx}\cos u=-\operatorname{sen}(u)\frac{du}{dx}$		(3.574)
	$\displaystyle\frac{d}{dx}\operatorname{tg}u=\sec^{2}(u)\frac{du}{dx}$		(3.575)
	$\displaystyle\frac{d}{dx}\operatorname{cotg}u=-\operatorname{cossec}^{2}(u)% \frac{du}{dx}$		(3.576)
	$\displaystyle\frac{d}{dx}\sec u=\sec(u)\operatorname{tg}(u)\frac{du}{dx}$		(3.577)
	$\displaystyle\frac{d}{dx}\operatorname{cossec}u=-\operatorname{cossec}(u)% \operatorname{cotg}(u)\frac{du}{dx}$		(3.578)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{sen}u=\frac{1}{\sqrt{% 1-u^{2}}}\frac{du}{dx}$		(3.579)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\cos u=-\frac{1}{\sqrt{1-u^{2}}}% \frac{du}{dx}$		(3.580)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{tg}u=\frac{1}{1+u^{2}% }\frac{du}{dx}$		(3.581)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{cotg}u=-\frac{1}{1+u^% {2}}\frac{du}{dx}$		(3.582)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\sec u=\frac{1}{\|u\|\sqrt{u^{2}-1}}% \frac{du}{dx}$		(3.583)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{cossec}u=-\frac{1}{\|u% \|\sqrt{u^{2}-1}}\frac{du}{dx}$		(3.584)

3.9.3 Exercícios resolvidos

ER 3.9.1.

Calcule a equação da reta tangente ao gráfico da função $f(x)=\ln x$ no ponto $x=1$ . Faça, então, um esboço dos gráficos da função e da reta tangente.

Resolução.

A equação da reta tangente ao gráfico da função $f(x)=\ln x$ no ponto $x_{0}=1$ é

	$\displaystyle y=f^{\prime}(x_{0})(x-x_{0})+f(x_{0})$		(3.585)
	$\displaystyle y=f^{\prime}(1)(x-1)+f(1).$		(3.586)

Observando que

f^{\prime}(x)=(\ln x)^{\prime}=\frac{1}{x},

(3.587)

temos que a equação da reta tangente é

	$\displaystyle y=\frac{1}{1}(x-1)+\ln 1$		(3.588)
	$\displaystyle y=x-1.$		(3.589)

Na Figura 3.12, temos os gráficos da função e de sua reta tangente no ponto $x=1$ .

Código 74: Python

⬇

1from sympy import log, diff

2from sympy.abc import x

3rt = diff(log(x)).subs(x,1)*(x-1)+log(1)

4print("y = %s" % rt)

y = x - 1

ER 3.9.2.

Resolva a equação

\frac{d}{dx}\operatorname{arc}\operatorname{tg}x=1.

(3.590)

Resolução.

Lembrando que

\frac{d}{dx}\operatorname{arc}\operatorname{tg}x=\frac{1}{1+x^{2}},

(3.591)

temos

	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{tg}x=1$		(3.592)
	$\displaystyle\frac{1}{1+x^{2}}=1$		(3.593)
	$\displaystyle 1+x^{2}=1$		(3.594)
	$\displaystyle x^{2}=0$		(3.595)
	$\displaystyle x=0.$		(3.596)

3.9.4 Exercícios

E. 3.9.1.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=\log_{2}x^{2}$
b)

$g(x)=\ln(xe^{x})$

a) $\displaystyle f^{\prime}(x)=\frac{2}{x\ln 2}$ ; b) $g^{\prime}(x)=\frac{1+x}{x}$

E. 3.9.2.

Calcule a derivada em relação a $x$ das seguintes funções:

a)

$f(x)=\sqrt[3]{x^{2}}$
b)

$g(x)=(1+2x)^{e}$

a) $\displaystyle f^{\prime}(x)=\frac{2}{3\sqrt[3]{x}}$ ; b) $g^{\prime}(x)=2e(1+2x)^{e-1}$

E. 3.9.3.

Encontre a equação da reta tangente ao gráfico de $f(x)=\operatorname{arc}\operatorname{tg}x$ no ponto $x=0$ .

$y=x$

E. 3.9.4.

Mostre que valem as seguintes derivadas

	$\displaystyle\frac{d}{dx}\operatorname{arc}\cos x=-\frac{1}{\sqrt{1-x^{2}}}$		(3.597)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{cotg}x=-\frac{1}{1+x^% {2}}$		(3.598)

Dica: basta usar (3.527) com as funções trigonométricas inversas correspondentes.

E. 3.9.5.

Mostre que valem as seguintes derivadas

	$\displaystyle\frac{d}{dx}\operatorname{arc}\sec x=\frac{1}{\|x\|\sqrt{x^{2}-1}}$		(3.600)
	$\displaystyle\frac{d}{dx}\operatorname{arc}\operatorname{cossec}x=-\frac{1}{\|x% \|\sqrt{x^{2}-1}}$		(3.601)

Dica: basta usar (3.527) com as funções trigonométricas inversas correspondentes.

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Cálculo I

3.9 Diferenciabilidade da função inversa

Exemplo 3.9.1.

Observação 3.9.1.(Derivada da função logarítmica)

Exemplo 3.9.2.

3.9.1 Derivadas de funções trigonométricas inversas

Exemplo 3.9.3.

Exemplo 3.9.4.

3.9.2 Lista de derivadas

3.9.3 Exercícios resolvidos

ER 3.9.1.

Resolução.

ER 3.9.2.

Resolução.

3.9.4 Exercícios

E. 3.9.1.

E. 3.9.2.

E. 3.9.3.

E. 3.9.4.

E. 3.9.5.

Envie seu comentário