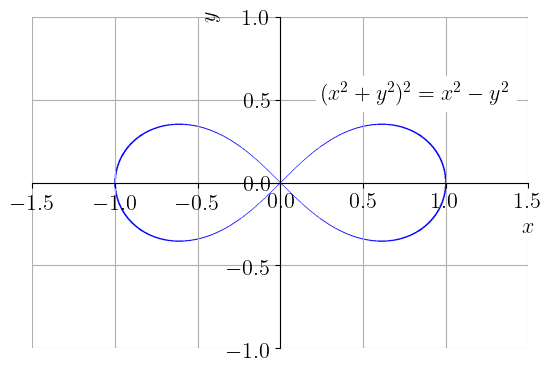Cálculo I

3 Derivadas 3.9 Diferenciabilidade da função inversa 4 Aplicações da derivada

Material disponível para compra: apostila. Consulte outras formas de colaboração aqui!

3.10 Derivação implícita

Seja $y=y(x)$ definida implicitamente por

g(y(x))=0.

(3.599)

A derivada $\mathrm{d}y/\mathrm{d}x$ pode ser calculada via regra da cadeia

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}g(y(x))=\frac{\mathrm{d}0}{\mathrm{% d}x}$		(3.600)
	$\displaystyle g^{\prime}(y(x))\frac{\mathrm{d}y}{\mathrm{d}x}=0.$		(3.601)

Exemplo 3.10.1.

Considere a equação da circunferência unitária (Figura 3.13)

x^{2}+y^{2}=1.

(3.602)

Aqui, vamos calcular $\mathrm{d}y/\mathrm{d}x$ de duas maneiras diferentes.

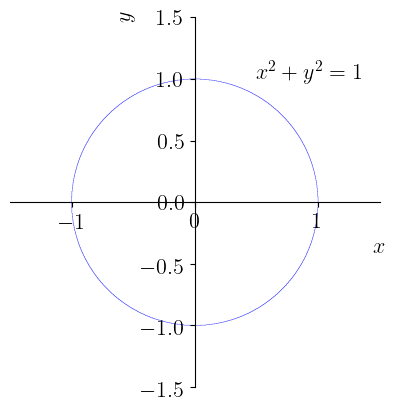Figura 3.13: Gráfico da circunferência unitária $x^{2}+y^{2}=1$ .

a)

Por derivação direta. Isolando $y$ em (3.602), temos

$y=\pm\sqrt{1-x^{2}}$ (3.603)

o que está bem definido para $-1\leq x\leq 1$ . Calculando a derivada, obtemos

$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}}{\mathrm{d}x}% \left(\pm\sqrt{1-x^{2}}\right)$ (3.604)

$\displaystyle\text{}\quad=\pm\frac{-2x}{2\sqrt{1-x^{2}}}$ (3.605)

$\displaystyle\text{}\quad=\mp\frac{x}{y}$ (3.606)

Ou seja, para $y<0$ , temos $y^{\prime}=x/y$ e, para $y>0$ , temos $y^{\prime}=-x/y$ . Logo, concluímos que

$\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x}{y}.$ (3.607)
b)

Por derivação implícita. Derivamos ambos os lados da (3.602) em relação a $x$

$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(x^{2}+y^{2}\right)=\frac{% \mathrm{d}1}{\mathrm{d}x}$ (3.608)

$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(x^{2}\right)+\frac{\mathrm{d}% }{\mathrm{d}x}\left(y^{2}(x)\right)=0$ (3.609)

$\displaystyle 2x+\frac{\mathrm{d}y^{2}}{\mathrm{d}y}\frac{\mathrm{d}y}{\mathrm% {d}x}=0$ (3.610)

$\displaystyle 2x+2y\frac{\mathrm{d}y}{\mathrm{d}x}=0$ (3.611)

$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x}{y}.$ (3.612)

Observação 3.10.1.(Derivadas de potências racionais de $x$ )

Vamos mostrar que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}\frac{\mathrm{% d}}{\mathrm{d}x}x^{r}=rx^{r-1}},

(3.613)

para qualquer número racional $r\neq 0$ . Denotando $r=m/n$ , $m,n\in\mathbb{N}$ , temos

	$\displaystyle y=x^{m/n}$		(3.614)
	$\displaystyle\Leftrightarrow$		(3.615)
	$\displaystyle y^{n}=x^{m}$		(3.616)

Da derivação de função potência com exponente inteiro, temos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}y^{n}=\frac{\mathrm{d}}{\mathrm{d}x% }x^{m}$		(3.617)
	$\displaystyle ny^{n-1}\frac{\mathrm{d}y}{\mathrm{d}x}=mx^{m-1}$		(3.618)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{m}{n}x^{m-1}y^{1-n}$		(3.619)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{m}{n}x^{m-1}\left(x^{\frac{% m}{n}}\right)^{1-n}$		(3.620)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{m}{n}x^{m-1}x^{\frac{m}{n}(% 1-n)}$		(3.621)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{m}{n}x^{m-1+\frac{m}{n}(1-n)}$		(3.622)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{m}{n}x^{\frac{m}{n}-1}.$		(3.623)

Logo, segue o resultados que queríamos demonstrar.

Exemplo 3.10.2.

Vamos calcular $\displaystyle\frac{\mathrm{d}^{2}y}{\mathrm{d}x^{2}}$ para

x^{2}+y^{2}=1.

(3.624)

Primeiramente, precisamos calcular $\mathrm{d}y/\mathrm{d}x$ . Isso foi feito no Exemplo 3.10.1, onde obtivemos

\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x}{y}.

(3.625)

Antes de derivarmos novamente, vamos reescrever essa última expressão da seguinte forma

y\frac{\mathrm{d}y}{\mathrm{d}x}=-x

(3.626)

Derivando

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left[y\frac{\mathrm{d}y}{\mathrm{d% }x}\right]=\frac{\mathrm{d}}{\mathrm{d}x}\left[-x\right]$		(3.627)
	$\displaystyle 1\frac{\mathrm{d}y}{\mathrm{d}x}\frac{\mathrm{d}y}{\mathrm{d}x}+% \frac{\mathrm{d}}{\mathrm{d}x}\frac{\mathrm{d}y}{\mathrm{d}x}=-1$		(3.628)
	$\displaystyle\left(\frac{\mathrm{d}y}{\mathrm{d}x}\right)^{2}+\frac{\mathrm{d}% ^{2}y}{\mathrm{d}x^{2}}=-1$		(3.629)
	$\displaystyle\frac{\mathrm{d}^{2}y}{\mathrm{d}x^{2}}=-\frac{x^{2}}{y^{2}}-1.$		(3.630)

3.10.1 Exercícios resolvidos

ER 3.10.1.

Calcule $\mathrm{d}y/\mathrm{d}x$ para a lemniscata de Bernoulli¹⁰¹⁰10Jacob Bernoulli, 1655-1705, matemático suíço. Fonte: Wikipédia: Jakob Bernoulli.

(x^{2}+y^{2})^{2}=x^{2}-y^{2}.

(3.631)

Consulte o gráfico da lemniscata na Figura 3.14.

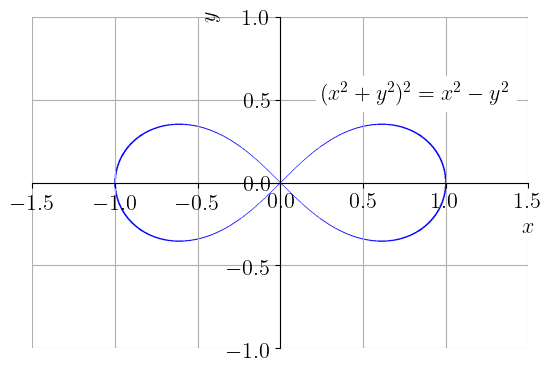Figura 3.14: Gráfico da lemniscata de Bernoulli $(x^{2}+y^{2})^{2}=x^{2}-y^{2}$ .

Resolução.

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left[(x^{2}+y^{2})^{2}\right]=% \frac{\mathrm{d}}{\mathrm{d}x}\left[x^{2}-y^{2}\right]$		(3.632)
	$\displaystyle 2(x^{2}+y^{2})\left(2x+2y\frac{\mathrm{d}y}{\mathrm{d}x}\right)=% 2x-2y\frac{\mathrm{d}y}{\mathrm{d}x}$		(3.633)

Rearranjando os termos, obtemos

2(y+2x^{2}y+2y^{2})\frac{\mathrm{d}y}{\mathrm{d}x}=2x-4xy^{2}-4x^{3}

(3.634)

ou ainda

\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{x-2x^{3}-2xy^{2}}{y+2x^{2}y+2y^{3}}

(3.635)

ER 3.10.2.

Calcule a equação da reta tangente ao gráfico da circunferência unitária

x^{2}+y^{2}=1

(3.636)

no ponto $\displaystyle\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)$ .

Resolução.

A equação da reta tangente ao gráfico de uma função $y=y(x)$ no ponto $(x_{0},y(x_{0}))$ é dada por

y=y^{\prime}(x_{0})(x-x_{0})+y(x_{0})

(3.637)

onde, nesse caso, $\displaystyle x_{0}=\frac{\sqrt{2}}{2}$ , $\displaystyle y(x_{0})=\frac{\sqrt{2}}{2}$

y^{\prime}(x_{0})=\left.\frac{\mathrm{d}y}{\mathrm{d}x}\right|_{x=x_{0}}.

(3.638)

Calculamos $\mathrm{d}y/\mathrm{d}x$ como segue

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(x^{2}+y^{2}\right)=\frac{% \mathrm{d}1}{\mathrm{d}x}$		(3.639)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(x^{2}\right)+\frac{\mathrm{d}% }{\mathrm{d}x}\left(y^{2}(x)\right)=0$		(3.640)
	$\displaystyle 2x+\frac{\mathrm{d}y^{2}}{\mathrm{d}y}\frac{\mathrm{d}y}{\mathrm% {d}x}=0$		(3.641)
	$\displaystyle 2x+2y\frac{\mathrm{d}y}{\mathrm{d}x}=0$		(3.642)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x}{y}.$		(3.643)

Com isso, temos

	$\displaystyle y^{\prime}(x_{0})=-\frac{x_{0}}{y(x_{0})}$		(3.644)
	$\displaystyle\text{}\quad=-\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}$		(3.645)
	$\displaystyle\text{}\quad=-1.$		(3.646)

Concluímos que a equação da reta tangente é

	$\displaystyle y=-1\cdot\left(x-\frac{\sqrt{2}}{2}\right)+\frac{\sqrt{2}}{2}$		(3.647)
	$\displaystyle y=-x+\sqrt{2}.$		(3.648)

ER 3.10.3.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}x^{x}.

(3.649)

Resolução.

Observamos que

	$\displaystyle y=x^{x}$		(3.650)
	$\displaystyle\ln y=\ln x^{x}$		(3.651)
	$\displaystyle\ln y=x\ln x.$		(3.652)

Agora, derivando em relação a $x$ ambos os lados desta equação, obtemos

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\ln y=\frac{\mathrm{d}}{\mathrm{d}x% }\left(x\ln x\right)$		(3.653)
	$\displaystyle\frac{1}{y}\frac{\mathrm{d}y}{\mathrm{d}x}=\ln(x)+1$		(3.654)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=y(1+\ln x)$		(3.655)
	$\displaystyle\frac{\mathrm{d}x^{x}}{\mathrm{d}x}=x^{x}(1+\ln x).$		(3.656)

3.10.2 Exercícios

E. 3.10.1.

Calcule $\mathrm{d}y/\mathrm{d}x$ para:

a)

$x+2xy-x^{3}=3$
b)

$x^{2}+y^{2}=xy$

a) $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{3x^{2}-2y-1}{2x}$ b) $\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{y-2x}{2y-x}$

E. 3.10.2.

Calcule $\mathrm{d}^{2}y/\mathrm{d}x^{2}$ para

x+2xy-x^{3}=3

(3.657)

$\displaystyle\frac{\mathrm{d}^{2}y}{\mathrm{d}x^{2}}=\frac{2y+1}{x^{2}}$

E. 3.10.3.

Encontre o ponto de interseção das retas tangentes ao gráfico de

y^{2}=x-1

(3.658)

nos pontos $(2,-1)$ e $(2,1)$ .

(0, 0)

E. 3.10.4.

Encontre a equação da reta tangente ao gráfico da circunferência de centro $C=(1,1)$ e raio $r=\sqrt{2}$ que passa pela origem $O=(0,0)$ .

$y=-x$

E. 3.10.5.

Seja $c$ a circunferência de raio $r>0$

x^{2}+y^{2}=r^{2}.

(3.659)

Mostra que a reta tangente ao gráfico de $c$ em qualquer ponto arbitrário $P=(x_{0},y_{0})\in c$ é perpendicular a reta $\overline{OP}$ , i.e. a reta que passa pela origem $O=(0,0)$ e pelo ponto $P .$

E. 3.10.6.

Calcule

\frac{\mathrm{d}}{\mathrm{d}x}(1+x)^{x}.

(3.660)

$x(1+x)^{x-1}+(1+x)^{x}\ln(1+x)$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Cálculo I

3.10 Derivação implícita

Exemplo 3.10.1.

Observação 3.10.1.(Derivadas de potências racionais de $x$ )

Exemplo 3.10.2.

3.10.1 Exercícios resolvidos

ER 3.10.1.

Resolução.

ER 3.10.2.

Resolução.

ER 3.10.3.

Resolução.

3.10.2 Exercícios

E. 3.10.1.

E. 3.10.2.

E. 3.10.3.

E. 3.10.4.

E. 3.10.5.

E. 3.10.6.

Envie seu comentário

	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}}{\mathrm{d}x}% \left(\pm\sqrt{1-x^{2}}\right)$		(3.604)
	$\displaystyle\text{}\quad=\pm\frac{-2x}{2\sqrt{1-x^{2}}}$		(3.605)
	$\displaystyle\text{}\quad=\mp\frac{x}{y}$		(3.606)

	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(x^{2}+y^{2}\right)=\frac{% \mathrm{d}1}{\mathrm{d}x}$		(3.608)
	$\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\left(x^{2}\right)+\frac{\mathrm{d}% }{\mathrm{d}x}\left(y^{2}(x)\right)=0$		(3.609)
	$\displaystyle 2x+\frac{\mathrm{d}y^{2}}{\mathrm{d}y}\frac{\mathrm{d}y}{\mathrm% {d}x}=0$		(3.610)
	$\displaystyle 2x+2y\frac{\mathrm{d}y}{\mathrm{d}x}=0$		(3.611)
	$\displaystyle\frac{\mathrm{d}y}{\mathrm{d}x}=-\frac{x}{y}.$		(3.612)

Política de uso de dados

Política de uso de dados

Cálculo I

3.10 Derivação implícita

Exemplo 3.10.1.

Observação 3.10.1.(Derivadas de potências racionais de x)

Exemplo 3.10.2.

3.10.1 Exercícios resolvidos

ER 3.10.1.

Resolução.

ER 3.10.2.

Resolução.

ER 3.10.3.

Resolução.

3.10.2 Exercícios

E. 3.10.1.

E. 3.10.2.

E. 3.10.3.

E. 3.10.4.

E. 3.10.5.

E. 3.10.6.

Envie seu comentário

Observação 3.10.1.(Derivadas de potências racionais de $x$ )