Cálculo I

4 Aplicações da derivada 4.4 Teste da primeira derivada 4.6 Taxas relacionadas

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.5 Concavidade e o teste da segunda derivada

O gráfico de uma função diferenciável $f$ é

a)

côncavo para cima em um intervalo aberto $I$ , se $f^{\prime}$ é crescente em $I$ ;
b)

côncavo para baixo em um intervalo aberto $I$ , se $f^{\prime}$ é decrescente em $I$ .

Assumindo que $f$ é duas vezes diferenciável, temos que a monotonicidade de $f^{\prime}$ está relacionada ao sinal de $f^{\prime\prime}$ (a segunda derivada de $f$ ). Logo, o gráfico de $f$ é

a)

côncavo para cima em um intervalo aberto $I$ , se $f^{\prime\prime}>0$ em $I$ ;
b)

côncavo para baixo em um intervalo aberto $I$ , se $f^{\prime\prime}<0$ em $I$ .

Exemplo 4.5.1.

Estudemos os seguintes casos:

a)

o gráfico de $f(x)=x^{2}$ é uma parábola côncava para cima em toda parte (Figura 4.16).

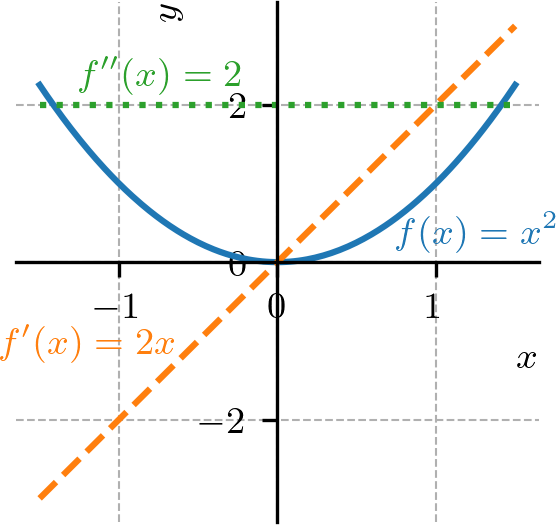
Figura 4.16: Gráfico de $f(x)=x^{2}$ e suas derivadas de ordem 1 e 2.

De fato, temos

$f^{\prime}(x)=2x,$ (4.132)

uma função crescente em toda parte. Também, temos

$f^{\prime\prime}(x)=2>0,$ (4.133)

em toda parte.
b)

o gráfico de $g(x)=-x^{2}$ é uma parábola côncava para baixo em toda parte. De fato, temos

$g^{\prime}(x)=-2x,$ (4.134)

uma função decrescente em toda parte. Também, temos

$g^{\prime\prime}(x)=-2<0,$ (4.135)

em toda parte. Faça os gráficos de $g$ , $g^{\prime}$ e $g^{\prime\prime}$ para melhor entender as relações entre a função e suas derivadas neste caso.
c)

o gráfico da função $h(x)=x^{3}$ é côncavo para baixo em $(-\infty,0)$ e côncavo para cima em $(0,\infty)$ . Consultemos a Figura 4.17.

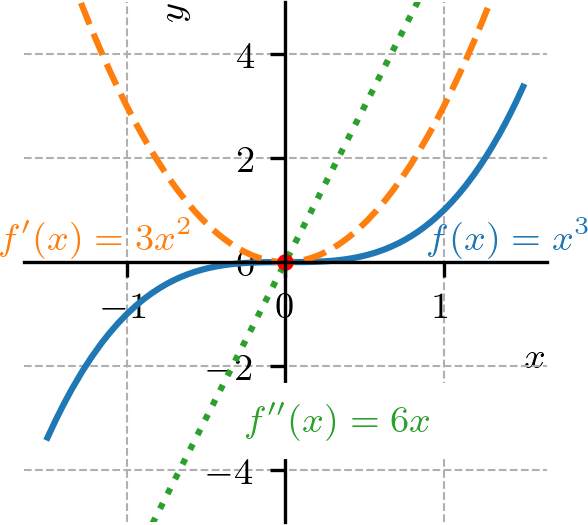
Figura 4.17: Gráfico de $h(x)=x^{3}$ e suas derivadas de ordem 1 e 2.

De fato, temos

$h^{\prime}(x)=x^{2},$ (4.136)

que é uma função decrescente em $(-\infty,0]$ e crescente em $[0,\infty)$ . Também, temos

$h^{\prime\prime}(x)=2x$ (4.137)

que assume valores negativos em $(-\infty,0)$ e valores positivos em $(0,\infty)$ .

Um ponto em que o gráfico de uma função $f$ muda de concavidade é chamado de ponto de inflexão. Em tais pontos temos

f^{\prime\prime}=0\quad\text{ou}\quad\nexists f^{\prime\prime}.

(4.138)

Exemplo 4.5.2.

Vejamos os seguintes casos:

a)

O gráfico da função $f(x)=x^{3}$ tem $x=0$ como único ponto de inflexão (consultemos a Figura 4.17). De fato, temos

$f^{\prime}(x)=3x^{2}$ (4.139)

que é diferenciável em toda parte com

$f^{\prime\prime}(x)=6x.$ (4.140)

Logo, os pontos de inflexão ocorrem quando

$\displaystyle f^{\prime\prime}(x)=0$ (4.141)

$\displaystyle 6x=0$ (4.142)

$\displaystyle x=0.$ (4.143)
b)

O gráfico da função $g(x)=\sqrt[3]{x}$ tem $x=0$ como único ponto de inflexão (consultemos a Figura 4.18).

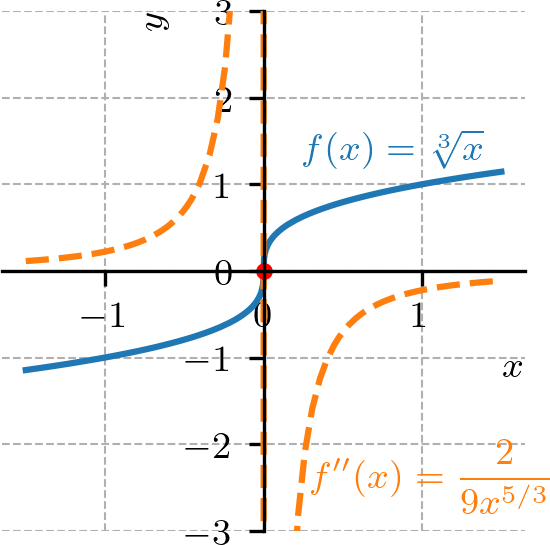
Figura 4.18: Gráfico de $g(x)=\sqrt[3]{x}$ e sua segunda derivada.

De fato, temos

$g^{\prime}(x)=\frac{1}{3}x^{-\frac{2}{3}},$ (4.144)

para $x\neq 0$ . Segue que

$g^{\prime\prime}(x)=-\frac{2}{9}x^{-\frac{5}{3}},$ (4.145)

para $x\neq 0$ , donde $g^{\prime\prime}>0$ em $(-\infty,0)$ e $g^{\prime\prime}<0$ em $(0,\infty)$ . Isto é, o gráfico de $g$ muda de concavidade em $x=0$ , $\nexists g^{\prime\prime}(0)$ , sendo $g$ côncava para cima em $(-\infty,0)$ e côncava para baixo em $(0,\infty)$ .

4.5.1 Teste da segunda derivada

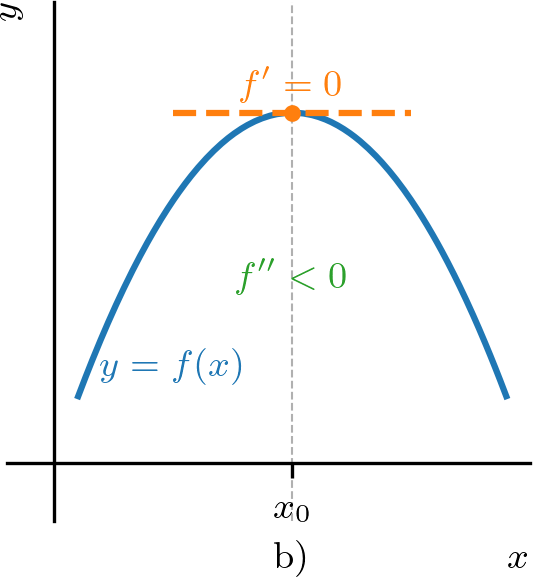
Seja $x=x_{0}$ um ponto crítico de uma dada função $f$ duas vezes diferenciável e $f^{\prime\prime}$ contínua em um intervalo aberto contendo $x=x_{0}$ . Temos

a)

se $f^{\prime}(x_{0})=0$ e $f^{\prime\prime}(x_{0})>0$ , então $x=x_{0}$ é um ponto de mínimo local de $f$ (Figura 4.19 a));
b)

se $f^{\prime}(x_{0})=0$ e $f^{\prime\prime}(x_{0})<0$ , então $x=x_{0}$ é um ponto de máximo local de $f$ (Figura 4.19 b)).

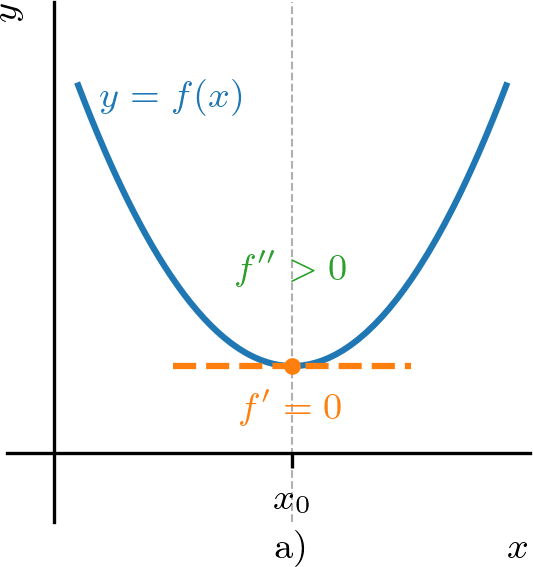
Refer to caption — Figura 4.19: Teste da segunda derivada: a) ponto de mínimo local; b) ponto de máximo local.

Exemplo 4.5.3.

A função $f(x)=2x^{3}-9x^{2}+12x-2$ tem pontos críticos

	$\displaystyle f^{\prime}(x)=6x^{2}-18x+12=0$		(4.146)
	$\displaystyle x^{2}-3x+2=0$		(4.147)
	$\displaystyle x=\frac{3\pm\sqrt{1}}{2}$		(4.148)
	$\displaystyle x_{1}=1\text{ ou }x_{2}=2.$		(4.149)

A segunda derivada de $f$ é

f^{\prime\prime}(x)=12x-18.

(4.150)

Logo, como $f^{\prime\prime}(x_{1})=f^{\prime\prime}(1)=-6<0$ , temos que $x_{1}=1$ é ponto de máximo local de $f$ . E, como $f^{\prime\prime}(x_{2})=f^{\prime\prime}(2)=6>0$ , temos que $x_{2}=2$ é ponto de mínimo local de $f$ . Verifiquemos no gráfico de $f$ (Figura 4.20).

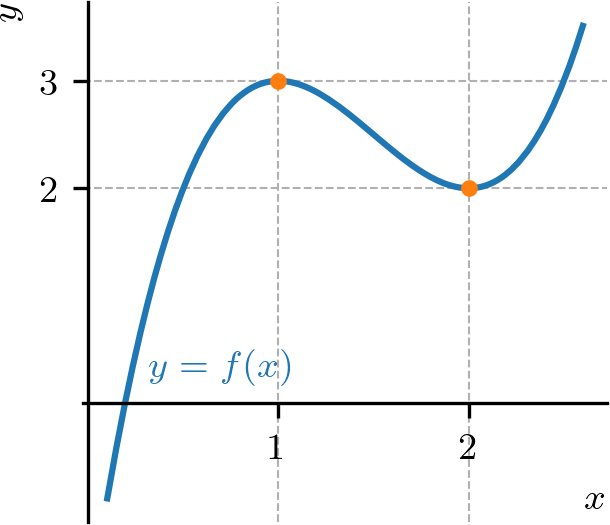
Observação 4.5.1.

Se $f^{\prime}(x_{0})=0$ e $f^{\prime\prime}(x_{0})=0$ , então $x=x_{0}$ pode ser ponto extremo local de $f$ ou não. Ou seja, o teste é inconclusivo.

Exemplo 4.5.4.

Vejamos os seguintes casos:

a)

A função $f(x)=x^{3}$ tem ponto crítico

$\displaystyle f^{\prime}(x)=0$ (4.151)

$\displaystyle 3x^{2}=0$ (4.152)

$\displaystyle x=0.$ (4.153)

Neste ponto, temos

$\displaystyle f^{\prime\prime}(x)=6x$ (4.154)

$\displaystyle f^{\prime\prime}(0)=0.$ (4.155)

Neste caso, $x=0$ não é ponto de extremo local e temos $f^{\prime}(0)=0$ e $f^{\prime\prime}(0)=0$ . Faça o gráfico de $f(x)=x^{3}$ e verifique!
b)

A função $f(x)=x^{4}$ tem um ponto crítico

$\displaystyle f^{\prime}(x)=0$ (4.156)

$\displaystyle 4x^{3}=0$ (4.157)

$\displaystyle x=0.$ (4.158)

Neste ponto, temos

$\displaystyle f^{\prime\prime}(x)=12x^{2}$ (4.159)

$\displaystyle f^{\prime\prime}(0)=0.$ (4.160)

Neste caso, $x=0$ é ponto de mínimo local e temos $f^{\prime}(0)=0$ e $f^{\prime\prime}(0)=0$ . Faça o gráfico de $f(x)=x^{4}$ e verifique!

4.5.2 Exercícios resolvidos

ER 4.5.1.

Encontre o valor máximo global de $f(x)=(x-1)e^{-x}$ .

Resolução.

Como $f$ é diferenciável em toda parte, temos que seu valor máximo (se existir) ocorre em ponto crítico tal que

	$\displaystyle f^{\prime}(x)=0$		(4.161)
	$\displaystyle(2-x)e^{-x}=0$		(4.162)
	$\displaystyle 2-x=0$		(4.163)
	$\displaystyle x=2.$		(4.164)

Agora, usando o teste da segunda derivada, temos

	$\displaystyle f^{\prime\prime}(x)=(x-3)e^{-x}$		(4.165)
	$\displaystyle f^{\prime\prime}(2)=-e^{-2}<0.$		(4.166)

Logo, $x=2$ é ponto de máximo local. O favor da função neste ponto é $f(2)=e^{-2}$ . Ainda, temos

	$\displaystyle\lim_{x\to-\infty}(x-1)e^{-x}=-\infty,$		(4.167)
	$\displaystyle\lim_{x\to\infty}(x-1)e^{-x}=0.$		(4.168)

Por tudo isso, concluímos que o valor máximo global de $f$ é $f(2)=e^{-2}$ .

Código 40: Python

⬇

1from sympy import Symbol, lambdify, exp, diff, solve

2x = Symbol('x')

3f = (x-1)*exp(-x)

4fl = diff(f, x)

5xc = solve(fl, x)

6print("xc =", xc[0])

xc = 2

⬇

1fll = diff(fl, x)

2print("f''(xc) =", fll.subs(x, xc[0]))

f''(xc) = -exp(-2)

⬇

1from sympy import limit, oo

2print("lim_x->oo f(x) =", limit(f, x, oo))

3print("lim_x->-oo f(x) =", limit(f, x, -oo))

lim_x->oo f(x) = 0

lim_x->-oo f(x) = -oo

ER 4.5.2.

Determine e classifique os extremos da função

f(x)=x^{4}-4x^{3}+4x^{2}

(4.169)

restrita ao intervalo de $[-1,3]$ .

Resolução.

Como $f$ é diferenciável em $(-1,3)$ , temos que seus extremos locais ocorrem nos seguintes pontos críticos

	$\displaystyle f^{\prime}(x)=0$		(4.170)
	$\displaystyle 4x^{3}-12x^{2}+8x=0$		(4.171)
	$\displaystyle 4x(x^{2}-3x+2)=0$		(4.172)

logo os pontos críticos são $x_{1}=0$ , $x_{2}=1$ e $x_{3}=2$ . Calculando a segunda derivada de $f$ , temos

f^{\prime\prime}(x)=12x^{2}-24x+8.

(4.173)

Do teste da segunda derivada, temos

f^{\prime\prime}(x_{1})=f^{\prime\prime}(0)=8>0

(4.174)

donde temos que $x_{1}=0$ é ponto de mínimo local. Similarmente, temos

	$\displaystyle f^{\prime\prime}(x_{2})=f^{\prime\prime}(1)=-4<0,$		(4.175)
	$\displaystyle f^{\prime\prime}(x_{3})=f^{\prime\prime}(2)=8>0,$		(4.176)

done $x_{2}=1$ é ponto de máximo local e $x_{3}=2$ é ponto de mínimo local. Agora, vejamos os valores de $f$ em cada ponto de interesse.

$x$	$-1$	$0$	$1$	$2$	$3$
$f(x)$	$9$	$0$	$1$	$0$	$9$

Então, podemos concluir que $x=-1$ e $x=3$ são pontos de máximo global (o valor máximo global é $f(-1)=f(3)=9$ ), $x=1$ é ponto de máximo local, $x=0$ e $x=2$ são pontos de mínimo global (o valor mínimo global é $f(0)=f(2)=0$ ).

ER 4.5.3.

Uma cerca de $300$ m será usada para cercar as laterais e a parte traseira de um terreno retangular, deixando a frente aberta (conforme figura abaixo). Quais devem ser as dimensões do terreno para que a área seja máxima?

Resolução.

Conforme indicado na figura acima, consideremos um terreno retangular de comprimento $l$ e largura $w$ . A área do terreno é dada por

A=l\cdot w.

(4.177)

Como a cerca será usada para cercar as laterais e a parte traseira do terreno, temos a restrição

2w+l=300.

(4.178)

Logo, podemos escrever $l$ em função de $w$ como

l=300-2w.

(4.179)

Assim, a área do terreno pode ser escrita como função de $w$

A(w)=w(300-2w)=300w-2w^{2}.

(4.180)

Para encontrarmos o valor máximo da área, calculamos a derivada de $A$ em relação a $w$

\frac{\mathrm{d}A}{\mathrm{d}w}=300-4w.

(4.181)

O ponto crítico ocorre quando

	$\displaystyle\frac{\mathrm{d}A}{\mathrm{d}w}=0$		(4.182)
	$\displaystyle 300-4w=0$		(4.183)
	$\displaystyle w=75.$		(4.184)

Usando o teste da segunda derivada, temos

\frac{\mathrm{d}^{2}A}{\mathrm{d}w^{2}}=-4<0,

(4.185)

logo $w=75$ é ponto de máximo local. Os casos extremos quando $l=300$ ou $w=150$ podem ser descartados, pois implicam em $A=0$ . Finalmente, calculamos o comprimento $l$

	$\displaystyle l=300-2(75)$		(4.186)
	$\displaystyle l=150.$		(4.187)

Portanto, as dimensões do terreno para que a área seja máxima são: largura $w=75$ m e comprimento $l=150$ m.

4.5.3 Exercícios

E. 4.5.1.

Use o teste da segunda derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $f(x)=x^{2}-2x$ .

$x=1$ ponto de mínimo global

E. 4.5.2.

Use o teste da segunda derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $\displaystyle f(x)=\frac{x^{3}}{3}-x$ .

$x_{1}=-1$ ponto de máximo local; $x_{2}=1$ ponto de mínimo local;

E. 4.5.3.

Use o teste da segunda derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $\displaystyle f(x)=x^{2/3}(x-1)$ .

$x_{1}=0$ ponto de máximo local; $x_{2}=2/5$ ponto de mínimo local;

E. 4.5.4.

Seja $f(x)=-x^{4}$ . Mostre que $x=0$ é ponto de máximo local de $f$ e que $f^{\prime}(0)=f^{\prime\prime}(0)=0$ .

$f^{\prime}(x)=-4x^{3}$ , $f^{\prime}(0)=0$ . Pelo teste da 1. derivada, temos que $x=0$ é ponto de máximo local. $f^{\prime\prime}(x)=-12x^{2}$ , $f^{\prime\prime}(0)=0$ .

E. 4.5.5.

Quais são as dimensões (largura $w$ e altura $h$ ) do retângulo de maior área que pode ser construindo tendo perímetro $300$ m?

$w=75\text{m}$ , $h=75\text{m}$

E. 4.5.6.

Uma caixa aberta é feita a partir de uma folha retangular de papelão de comprimento $l=45$ cm e largura $w=30$ cm, cortando-se quadrados iguais de lado $x$ cm em cada canto e dobrando-se as abas formadas (consulte a figura abaixo). Encontre o valor de $x$ que resulte a caixa de maior volume possível.

$\displaystyle x=\frac{25-5\sqrt{7}}{2}\approx 5.89$ cm

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Cálculo I

4.5 Concavidade e o teste da segunda derivada

Exemplo 4.5.1.

Exemplo 4.5.2.

4.5.1 Teste da segunda derivada

Exemplo 4.5.3.

Observação 4.5.1.

Exemplo 4.5.4.

4.5.2 Exercícios resolvidos

ER 4.5.1.

Resolução.

ER 4.5.2.

Resolução.

ER 4.5.3.

Resolução.

4.5.3 Exercícios

E. 4.5.1.

E. 4.5.2.

E. 4.5.3.

E. 4.5.4.

E. 4.5.5.

E. 4.5.6.

Envie seu comentário

	$\displaystyle f^{\prime\prime}(x)=0$		(4.141)
	$\displaystyle 6x=0$		(4.142)
	$\displaystyle x=0.$		(4.143)

	$\displaystyle f^{\prime}(x)=0$		(4.151)
	$\displaystyle 3x^{2}=0$		(4.152)
	$\displaystyle x=0.$		(4.153)

	$\displaystyle f^{\prime\prime}(x)=6x$		(4.154)
	$\displaystyle f^{\prime\prime}(0)=0.$		(4.155)

	$\displaystyle f^{\prime}(x)=0$		(4.156)
	$\displaystyle 4x^{3}=0$		(4.157)
	$\displaystyle x=0.$		(4.158)

	$\displaystyle f^{\prime\prime}(x)=12x^{2}$		(4.159)
	$\displaystyle f^{\prime\prime}(0)=0.$		(4.160)