Cálculo I

4 Aplicações da derivada 4.3 Teorema do valor médio 4.5 Concavidade e o teste da segunda derivada

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

4.4 Teste da primeira derivada

Lembremos que os extremos de uma função ocorrem nos extremos de seu domínio ou em um ponto crítico. Aliado a isso, o Corolário 4.3.3 nos fornece condições suficientes para classificar os pontos críticos como extremos locais.

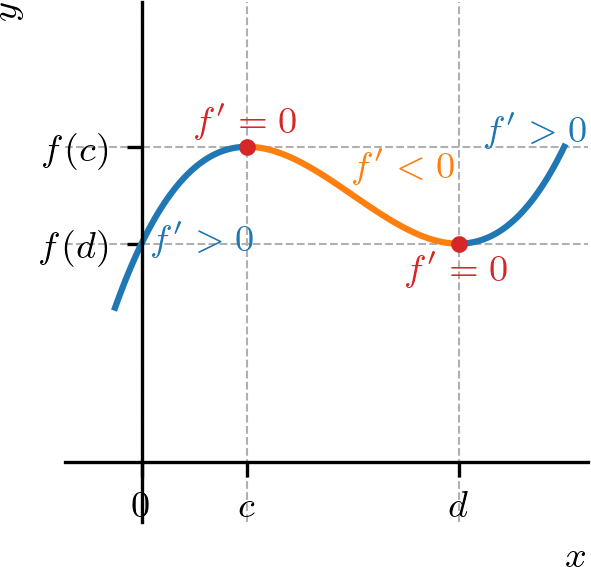
Mais precisamente, seja $c$ um ponto crítico de uma função contínua $f$ e diferenciável em todos os pontos de um intervalo aberto $(a,b)$ contendo $c$ , exceto possivelmente no ponto $c$ . Movendo-se no sentido positivo em $x$ :

•

se $f^{\prime}(x)$ muda de negativa para positiva em $c$ , então $f$ possui um mínimo local em $c$ ;
•

se $f^{\prime}(x)$ muda de positiva para negativa em $c$ , então $f$ possui um máximo local em $c$ ;
•

se $f^{\prime}$ não muda de sinal em $c$ , então $c$ não é um extremo local de $f$ .

Veja a Figura 4.14.

Refer to caption — Figura 4.14: Teste da primeira derivada: $c$ ponto de máximo local; $d$ ponto de mínimo local.

Exemplo 4.4.1.

Consideremos a função $\displaystyle f(x)=\frac{x^{3}}{3}-2x^{2}+3x+3$ . Como $f$ é diferenciável em toda parte, seus pontos críticos são aqueles tais que

f^{\prime}(x)=0.

(4.104)

Temos $f^{\prime}(x)=x^{2}-4x+3$ . Segue, que os pontos críticos são

	$\displaystyle x^{2}-4x+3=0$		(4.105)
	$\displaystyle x=\frac{4\pm\cancelto{2}{\sqrt{16-12}}}{2}$		(4.106)
	$\displaystyle x_{1}=1\text{ ou }x_{2}=3.$		(4.107)

Com isso, temos

Intervalo	$x<1$	$1<x<3$	$3<x$
$f^{\prime}$	+	-	+
$f$	crescente	decrescente	crescente

Então, do teste da primeira derivada, concluímos que $x_{1}=1$ é ponto de máximo local e que $x_{2}=3$ é ponto de mínimo local.

Código 38: Python

⬇

1from sympy import Symbol, lambdify, diff, solve, reduce_inequalities

2x = Symbol('x')

3fl = lambdify(x, diff(x**3/3 - 2*x**2 + 3*x + 3, x))

4xc = solve(fl(x), x)

5print("x1 =", xc[0])

6print("x2 =", xc[1])

7fl_neg = reduce_inequalities(fl(x) < 0, x)

8print("f' < 0 em:", fl_neg)

9fl_pos = reduce_inequalities(fl(x) > 0, x)

10print("f' > 0 em:", fl_pos)

x1 = 1

x2 = 3

f' < 0 em: (1 < x) & (x < 3)

f' > 0 em: ((-oo < x) & (x < 1)) | ((3 < x) & (x < oo))

4.4.1 Exercícios resolvidos

ER 4.4.1.

Determine e classifique os extremos da função

f(x)=x^{4}-4x^{3}+4x^{2}.

(4.108)

Resolução.

Como o domínio da $f$ é $(-\infty,\infty)$ e $f$ é diferenciável em toda parte, temos que seus extremos ocorrem em pontos críticos tais que

f^{\prime}(x)=0.

(4.109)

Resolvendo, obtemos

	$\displaystyle 4x^{3}-12x^{2}+8x=0$		(4.110)
	$\displaystyle 4x(x^{2}-3x+2)=0$		(4.111)

Logo, $4x=0$ ou $x^{2}-3x+2=0$ . Resolvendo cada uma das equações, temos $x_{1}=0$ ou

	$\displaystyle x^{2}-3x+2=0$		(4.112)
	$\displaystyle x=\frac{3\pm 1}{2}$		(4.113)
	$\displaystyle x_{2}=1\text{ ou }x_{3}=2.$		(4.114)

Portanto, os ponto críticos são $x_{1}=0$ , $x_{2}=1$ e $x_{3}=2$ . Fazendo o estudo de sinal da $f^{\prime}$ , temos

	$x<0$	$0<x<1$	$1<x<2$	$2<x$
$4x$	-	+	+	+
$x^{2}-3x+2$	+	+	-	+
$f^{\prime}(x)$	-	+	-	+
$f$	decrescente	crescente	decrescente	crescente

Então, do teste da primeira derivada, concluímos que $x_{1}=0$ é ponto de mínimo local, $x_{2}=1$ é ponto de máximo local e $x_{3}=2$ é ponto de mínimo local.

Código 39: Python

⬇

1from sympy import Symbol, Lambda, exp, diff

2x = Symbol('x')

3f = Lambda(x, x**4 - 4*x**3 + 4*x**2)

4print('f(x) =', f(x))

5fl = Lambda(x, diff(f(x), x))

6print("f'(x) =", fl(x))

f(x) = x**4 - 4*x**3 + 4*x**2

f'(x) = 4*x**3 - 12*x**2 + 8*x

⬇

1# pontos críticos de f

2from sympy import solve

3pc = solve(fl(x), x)

4print('pontos críticos:', pc)

pontos críticos: [0, 1, 2]

⬇

1# estudo de sinal de f'

2from sympy import reduce_inequalities

3# intervalo onde f' é positiva

4intervalos_pos = reduce_inequalities([fl(x) > 0], x)

5print('f\’ > 0 em', intervalos_pos)

6# intervalo onde f' é negativa

7intervalos_neg = reduce_inequalities([fl(x) < 0], x)

8print('f\’ < 0 em', intervalos_neg)

f' > 0 em ((0 < x) & (x < 1)) | ((2 < x) & (x < oo))

f' < 0 em ((-oo < x) & (x < 0)) | ((1 < x) & (x < 2))

ER 4.4.2.

Encontre o valor máximo global de $f(x)=(x-1)e^{-x}$ .

Resolução.

Como $f$ é diferenciável em toda parte, temos que seu máximo ocorre em ponto crítico tal que

	$\displaystyle f^{\prime}(x)=0$		(4.115)
	$\displaystyle(2-x)e^{-x}=0$		(4.116)
	$\displaystyle 2-x=0$		(4.117)
	$\displaystyle x=2.$		(4.118)

Fazendo o estudo de sinal da derivada, obtemos

	$x<0$	$0<x$
$f^{\prime}$	+	-
$f$	crescente	decrescente

Portanto, do teste da primeira derivada, podemos concluir que $x=2$ é ponto de máximo local. O favor da função neste ponto é $f(2)=e^{-2}$ . Ainda, temos

	$\displaystyle\lim_{x\to-\infty}(x-1)e^{-x}=-\infty,$		(4.119)
	$\displaystyle\lim_{x\to\infty}(x-1)e^{-x}=0.$		(4.120)

Por tudo isso, concluímos que o valor máximo global de $f$ é $f(2)=e^{-2}$ .

ER 4.4.3.(Aplicação na geometria)

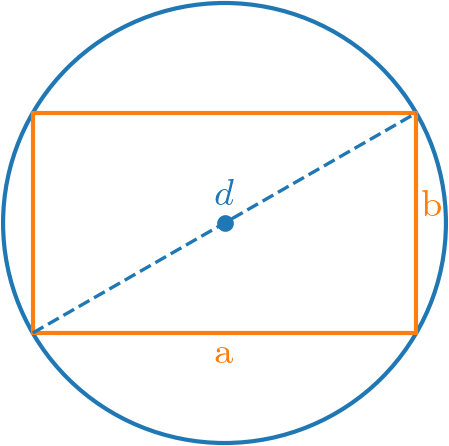
Mostre que o retângulo de maior área circunscrito em uma circunferência é um quadrado.

Resolução.

Na Figura 4.15, seja $d$ o diâmetro da circunferência e $a$ e $b$ as medidas dos lados do retângulo circunscrito. Queremos mostrar que $a=b$ . A área do retângulo é dada por

A=ab.

(4.121)

Note que, pelo Teorema de Pitágoras, temos

d^{2}=a^{2}+b^{2}.

(4.122)

Logo, podemos escrever $b$ em função de $a$ como

b=\sqrt{d^{2}-a^{2}}.

(4.123)

Assim, a área do retângulo pode ser escrita como função de $a$

A(a)=a\sqrt{d^{2}-a^{2}}.

(4.124)

Para encontrarmos o valor máximo da área, calculamos a derivada de $A$ em relação a $a$

	$\displaystyle\frac{\mathrm{d}A}{\mathrm{d}a}=\sqrt{d^{2}-a^{2}}-a\frac{2a}{2% \sqrt{d^{2}-a^{2}}}$		(4.125)
	$\displaystyle\text{}\quad=\frac{d^{2}-2a^{2}}{\sqrt{d^{2}-a^{2}}}.$		(4.126)

Os pontos críticos ocorrem quando

	$\displaystyle\frac{\mathrm{d}A}{\mathrm{d}a}=0$		(4.127)
	$\displaystyle d^{2}-2a^{2}=0$		(4.128)
	$\displaystyle a=\pm\frac{d}{\sqrt{2}}.$		(4.129)

O ponto crítico relevante é $\displaystyle a=d/\sqrt{2}$ , pois os lados são positivos. Fazendo o estudo de sinal da derivada (verifique!), concluímos que $\displaystyle a=d/\sqrt{2}$ é ponto de máximo local. Voltando a (4.123), temos

	$\displaystyle b=\sqrt{d^{2}-\left(\frac{d}{\sqrt{2}}\right)^{2}}$		(4.130)
	$\displaystyle\text{}\quad=\frac{d}{\sqrt{2}}.$		(4.131)

Portanto, $a=b$ e o retângulo de maior área circunscrito em uma circunferência é um quadrado.

4.4.2 Exercícios

E. 4.4.1.

Use o teste da primeira derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $f(x)=x^{2}-2x$ .

$x=1$ ponto de mínimo global

E. 4.4.2.

Use o teste da primeira derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $\displaystyle f(x)=\frac{x^{3}}{3}-x$ .

$x_{1}=-1$ ponto de máximo local; $x_{2}=1$ ponto de mínimo local;

E. 4.4.3.

Use o teste da primeira derivada para encontrar e classificar o(s) ponto(s) extremo(s) de $\displaystyle f(x)=x^{2/3}(x-1)$ .

$x_{1}=0$ ponto de máximo local; $x_{2}=2/5$ ponto de mínimo local;

E. 4.4.4.

Quais são as dimensões (largura $w$ e altura $h$ ) do retângulo de maior área que pode ser construindo tendo perímetro $300$ m?

$w=75\text{m}$ , $h=75\text{m}$

E. 4.4.5.

Uma caixa aberta é feita a partir de uma folha retangular de papelão de comprimento $l=45$ cm e largura $w=30$ cm, cortando-se quadrados iguais de lado $x$ cm em cada canto e dobrando-se as abas formadas (consulte a figura abaixo). Encontre o valor de $x$ que resulte a caixa de maior volume possível.

$\displaystyle x=\frac{25-5\sqrt{7}}{2}\approx 5.89$ cm

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Cálculo I

4.4 Teste da primeira derivada

Exemplo 4.4.1.

4.4.1 Exercícios resolvidos

ER 4.4.1.

Resolução.

ER 4.4.2.

Resolução.

ER 4.4.3.(Aplicação na geometria)

Resolução.

4.4.2 Exercícios

E. 4.4.1.

E. 4.4.2.

E. 4.4.3.

E. 4.4.4.

E. 4.4.5.

Envie seu comentário