Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.1 Combinação Linear
Dados vetores , , , e números reais , , , , com inteiro positivo, chamamos de
| (2.1) |
uma combinação linear de , , , . Neste caso, também dizemos que é gerado pelos vetores , , , ou, equivalentemente, que estes vetores geram o vetor .
Exemplo 2.1.1.
Sejam dados os vetores , , e . Então, temos:
-
a)
é uma combinação linear dos vetores e .
-
b)
é uma outra combinação linear dos vetores e .
-
c)
é uma combinação linear dos vetores , e .
-
d)
é uma combinação linear do vetor .
2.1.1 Interpretação Geométrica
Combinação Linear e Vetores Paralelos
Se é combinação linear não nula de apenas, então é paralelo a . De fato, se
| (2.2) |
com , então, por definição da multiplicação por escalar, tem a mesma direção de . Em outras palavras, temos a seguinte proposição. Consulte a Figura 2.1.
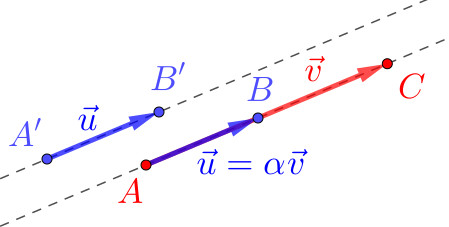
Proposição 2.1.1.
(Combinação Linear entre Vetores Paralelos.) Se são vetores não nulos tais que
| (2.3) |
com escalares não simultaneamente nulos, então .
Demonstração.
Sem perda de generalidade, vamos assumir que . Logo, temos que
| (2.4) |
o que mostra que têm a mesma direção de . ∎
Combinação Linear e Vetores Coplanares
Se é combinação linear não nula de e , então é coplanar a estes vetores. De fato, temos
| (2.6) |
com escalares . Se pelo menos um dos , , ou é nulo, então, é certo, que , e são coplanares. Caso sejam todos não nulos, e determinam um plano e um paralelogramo . Segue que
| (2.7) | ||||
| (2.8) | ||||
| (2.9) |
Concluímos que , e são coplanares.
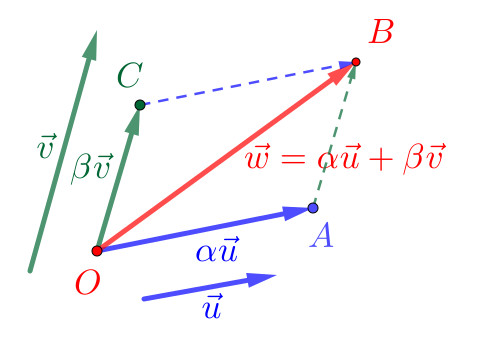
Proposição 2.1.2.
(Combinação Linear entre Vetores Coplanares.) Vetores , e não nulos têm combinação linear não trivial se, e somente se, são coplanares.
Demonstração.
Consulte o E.2.1.9. ∎
2.1.2 Exercícios Resolvidos
ER 2.1.1.
Com base na Figura 2.3, escreva o vetor como combinação linear dos vetores e .
Solução 0.
Para escrevermos o vetor como combinação linear dos vetores e , devemos determinar números e tais que
| (2.10) |
Com base na Figura 2.3, podemos tomar e , i.e. temos
| (2.11) |
ER 2.1.2.
Sabendo que , forneça três maneiras de escrever o vetor nulo como combinação linear dos vetores e .
Solução 0.
Dado que
| (2.12) |
podemos escrever como combinação linear de e das seguintes formas:
-
a)
subtraindo .
(2.13) (2.14) -
b)
subtraindo .
(2.15) (2.16) (2.17) -
c)
multiplicando por e subtraindo .
(2.18) (2.19) (2.20)
2.1.3 Exercícios
E. 2.1.1.
Com base na figura abaixo, escreva cada um dos seguintes vetores como combinação linear de e .
![[Uncaptioned image]](cap_base/dados/fig_comblin_exer_geo/fig.jpg)
-
a)
.
-
b)
.
-
c)
.
-
d)
.
Resposta 0.
a) . b) . c) . d) .
E. 2.1.2.
Com base na figura abaixo, escreva os seguintes vetores como combinação linear de e .
![[Uncaptioned image]](cap_base/dados/fig_comblin_exer_geo2/fig.jpg)
-
a)
.
-
b)
.
-
c)
.
-
d)
.
Resposta 0.
a) . b) . c) . d) .
E. 2.1.3.
Sabendo que , escreva como combinação linear de e .
Resposta 0.
E. 2.1.4.
Sejam e vetores de mesma direção e um vetor não paralelo a , todos não nulos. Pode-se escrever como combinação linear de e ? Justifique sua resposta.
Resposta 0.
Não.
E. 2.1.5.
Sejam e ambos não nulos e de mesma direção. Pode-se afirmar que gera ? Justifique sua resposta.
Resposta 0.
Sim.
E. 2.1.6.
Sejam e vetores não paralelos entre si e um vetor não coplanar a e , todos não nulos. É possível gerar com e ?
Resposta 0.
Não.
E. 2.1.7.
Sejam e não nulos, coplanares e com direções distintas. Se é um vetor também coplanar a e , então e geram ? Justifique sua resposta.
Resposta 0.
Sim.
E. 2.1.8.
Mostre que se são vetores não nulos e paralelos entre si, então existem escalares não simultaneamente nulos tais que
| (2.21) |
Resposta 0.
Sem perda de generalidade, existe tal que . Logo, escolhendo e , temos que .
E. 2.1.9.
Faça a demonstração da Proposição 2.1.2.
Resposta 0.
Implicação. Sem perda de generalidade, assumimos que , logo
| (2.22) |
o que mostra que é coplanar aos vetores e .
Recíproca. Se dois dos vetores forem paralelos entre si, o resultado segue da Proposição 2.1.1. Caso contrário, sejam e a reta paralela a que passa por . Seja, então, a interseção entre e a reta suporte de que passa por . Logo, existem tal que e . Segue que .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Vetores
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.1 Combinação Linear
Dados vetores , , , e números reais , , , , com inteiro positivo, chamamos de
| (2.1) |
uma combinação linear de , , , . Neste caso, também dizemos que é gerado pelos vetores , , , ou, equivalentemente, que estes vetores geram o vetor .
Exemplo 2.1.1.
Sejam dados os vetores , , e . Então, temos:
-
a)
é uma combinação linear dos vetores e .
-
b)
é uma outra combinação linear dos vetores e .
-
c)
é uma combinação linear dos vetores , e .
-
d)
é uma combinação linear do vetor .
2.1.1 Interpretação Geométrica
Combinação Linear e Vetores Paralelos
Se é combinação linear não nula de apenas, então é paralelo a . De fato, se
| (2.2) |
com , então, por definição da multiplicação por escalar, tem a mesma direção de . Em outras palavras, temos a seguinte proposição. Consulte a Figura 2.1.

Proposição 2.1.1.
(Combinação Linear entre Vetores Paralelos.) Se são vetores não nulos tais que
| (2.3) |
com escalares não simultaneamente nulos, então .
Demonstração.
Sem perda de generalidade, vamos assumir que . Logo, temos que
| (2.4) |
o que mostra que têm a mesma direção de . ∎
Combinação Linear e Vetores Coplanares
Se é combinação linear não nula de e , então é coplanar a estes vetores. De fato, temos
| (2.6) |
com escalares . Se pelo menos um dos , , ou é nulo, então, é certo, que , e são coplanares. Caso sejam todos não nulos, e determinam um plano e um paralelogramo . Segue que
| (2.7) | ||||
| (2.8) | ||||
| (2.9) |
Concluímos que , e são coplanares.

Proposição 2.1.2.
(Combinação Linear entre Vetores Coplanares.) Vetores , e não nulos têm combinação linear não trivial se, e somente se, são coplanares.
Demonstração.
Consulte o E.2.1.9. ∎
2.1.2 Exercícios Resolvidos
ER 2.1.1.
Com base na Figura 2.3, escreva o vetor como combinação linear dos vetores e .

Solução 0.
Para escrevermos o vetor como combinação linear dos vetores e , devemos determinar números e tais que
| (2.10) |
Com base na Figura 2.3, podemos tomar e , i.e. temos
| (2.11) |
ER 2.1.2.
Sabendo que , forneça três maneiras de escrever o vetor nulo como combinação linear dos vetores e .
Solução 0.
Dado que
| (2.12) |
podemos escrever como combinação linear de e das seguintes formas:
-
a)
subtraindo .
(2.13) (2.14) -
b)
subtraindo .
(2.15) (2.16) (2.17) -
c)
multiplicando por e subtraindo .
(2.18) (2.19) (2.20)
2.1.3 Exercícios
E. 2.1.1.
Com base na figura abaixo, escreva cada um dos seguintes vetores como combinação linear de e .
![[Uncaptioned image]](cap_base/dados/fig_comblin_exer_geo/fig.jpg)
-
a)
.
-
b)
.
-
c)
.
-
d)
.
Resposta 0.
a) . b) . c) . d) .
E. 2.1.2.
Com base na figura abaixo, escreva os seguintes vetores como combinação linear de e .
![[Uncaptioned image]](cap_base/dados/fig_comblin_exer_geo2/fig.jpg)
-
a)
.
-
b)
.
-
c)
.
-
d)
.
Resposta 0.
a) . b) . c) . d) .
E. 2.1.3.
Sabendo que , escreva como combinação linear de e .
Resposta 0.
E. 2.1.4.
Sejam e vetores de mesma direção e um vetor não paralelo a , todos não nulos. Pode-se escrever como combinação linear de e ? Justifique sua resposta.
Resposta 0.
Não.
E. 2.1.5.
Sejam e ambos não nulos e de mesma direção. Pode-se afirmar que gera ? Justifique sua resposta.
Resposta 0.
Sim.
E. 2.1.6.
Sejam e vetores não paralelos entre si e um vetor não coplanar a e , todos não nulos. É possível gerar com e ?
Resposta 0.
Não.
E. 2.1.7.
Sejam e não nulos, coplanares e com direções distintas. Se é um vetor também coplanar a e , então e geram ? Justifique sua resposta.
Resposta 0.
Sim.
E. 2.1.8.
Mostre que se são vetores não nulos e paralelos entre si, então existem escalares não simultaneamente nulos tais que
| (2.21) |
Resposta 0.
Sem perda de generalidade, existe tal que . Logo, escolhendo e , temos que .
E. 2.1.9.
Faça a demonstração da Proposição 2.1.2.
Resposta 0.
Implicação. Sem perda de generalidade, assumimos que , logo
| (2.22) |
o que mostra que é coplanar aos vetores e .
Recíproca. Se dois dos vetores forem paralelos entre si, o resultado segue da Proposição 2.1.1. Caso contrário, sejam e a reta paralela a que passa por . Seja, então, a interseção entre e a reta suporte de que passa por . Logo, existem tal que e . Segue que .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.