Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Método de Elementos Finitos

2 Problemas Bidimensionais 2.1 Malha e Espaço 2.3 Projeção

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.2 Interpolação

Em revisão

Dada uma função contínua $f$ em um triângulo $K$ com nodos $N_{i}$ , $i=0,1,2$ , sua interpolação linear $\pi f\in P_{1}(K)$ é definida por

\pi f=\sum_{i=0}^{2}f(N_{i})\varphi_{i}.

(2.10)

Logo, temos $\pi f(N_{i})=f(N_{i})$ para todo $i=0,1,2$ .

Exemplo 2.2.1.

Consideramos a função

u(x_{0},x_{1})=\operatorname{sen}(\pi x_{0})\cos(\pi x_{1})

(2.11)

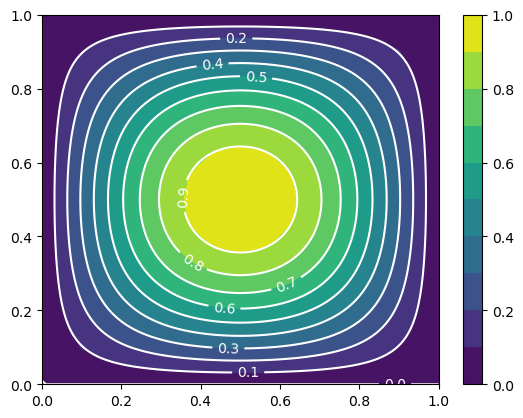
defina no domínio $D=[0,1]^{2}$ . O seguinte código computa a interpolação de $f$ no espaço de elementos finitos $V_{h}$ sobre uma malha uniforme de $16\times 16$ triângulos. Com ele, graficamos a função interpolada $u_{h}\in V_{h}$ e a função $u$ . Consulte a Fig. 2.3.

Refer to caption — Figura 2.3: Gráfico de comparação função interpolada $u_{h}\in V_{h}$ (gráfico de contornos em cores) e da função original $u$ (isolinhas) referentes ao Exemplo 2.2.1.

Código 9: interp2d.py

⬇

1from mpi4py import MPI

2from dolfinx import mesh

4# malha

5domain = mesh.create_unit_square(MPI.COMM_WORLD, 16, 16)

7from dolfinx import fem

9# espaço de elementos finitos

10V = fem.functionspace(domain, ("P",1))

12# função do espaço V

13uh = fem.Function(V)

15# interpolate

16import numpy as np

17def u(x, mod=np):

18 return mod.sin(mod.pi*x[0])*mod.sin(mod.pi*x[1])

20uh.interpolate(lambda x: u(x))

22# eval fun

23from dolfinx import geometry

25def fun_eval(u, points,

26 domain=domain):

27 u_values = []

28 bb_tree = geometry.bb_tree(domain, domain.topology.dim)

29 cells = []

30 points_on_proc = []

31 # Find cells whose bounding-box collide with the the points

32 cell_candidates = geometry.compute_collisions_points(bb_tree,

33 points.T)

34 # Choose one of the cells that contains the point

35 colliding_cells = geometry.compute_colliding_cells(domain,

36 cell_candidates,

37 points.T)

38 for i, point in enumerate(points.T):

39 if len(colliding_cells.links(i)) > 0:

40 points_on_proc.append(point)

41 cells.append(colliding_cells.links(i)[0])

43 points_on_proc = np.array(points_on_proc, dtype=np.float64)

44 u_values = u.eval(points_on_proc, cells)

45 return u_values

47# gráfico

48import numpy as np

49nx = ny = 101

50xx0 = np.linspace(0., 1., nx)

51xx1 = np.linspace(0., 1., ny)

52X0, X1 = np.meshgrid(xx0, xx1, indexing='ij')

53points = np.zeros((3, nx*ny))

54points[0] = X0.reshape(-1)

55points[1] = X1.reshape(-1)

57yh = fun_eval(uh, points)

58Yh = yh.reshape((nx,ny))

60import matplotlib.pyplot as plt

62fig = plt.figure()

63ax = fig.add_subplot()

64levels=10

65cb = ax.contourf(X0, X1, Yh, levels = levels)

66fig.colorbar(cb)

67Y = u([X0, X1])

68cl = ax.contour(X0, X1, Y, levels = levels, colors='w')

69ax.clabel(cl)

70plt.show()

Afim de determinarmos estimativas para o erro de interpolação, precisamos da chamada derivada total de primeira ordem

Df=\left(\left|\frac{\partial f}{\partial x_{0}}\right|^{2}+\left|\frac{% \partial f}{\partial x_{1}}\right|^{2}\right)^{1/2},

(2.12)

e da derivada total de segunda ordem

D^{2}f=\left(\left|\frac{\partial^{2}f}{\partial x_{0}^{2}}\right|^{2}+\left|% \frac{\partial^{2}f}{\partial x_{0}\partial x_{1}}\right|^{2}+\left|\frac{% \partial^{2}f}{\partial x_{1}^{2}}\right|^{2}\right)^{1/2}.

(2.13)

Proposição 2.2.1.

(Erro da interpolação no espaço linear.) A interpolação $\pi f$ satisfaz as seguintes estimativas

	$\displaystyle\\|f-\pi f\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}^{2}\\|D^{2}f\\|_{L^{2}(K)},$		(2.14)
	$\displaystyle\\|D(f-\pi f)\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}\\|D^{2}f\\|_{L^{2}(K)}.$		(2.15)

Demonstração.

Veja [1, Capítulo 4]. ∎

Observação 2.2.1.

A constante $C$ dependo do inverso de $\operatorname{sen}(\theta_{K})$ onde $\theta_{K}$ é o menor angulo de $K$ . Desta forma, para um triângulo com $\theta_{K}$ muito pequeno, as estimativas (2.14) e (2.15) perdem sentido. Este fato indica a necessidade de se trabalhar com malhas regulares.

A interpolação no espaço $V_{h}$ de uma dada função $f$ no domínio $\Omega$ é denotada também por $\pi f\in V_{h}$ e definida por

\pi f=\sum_{i=0}^{n_{p}-1}f(N_{i})\varphi_{i}.

(2.16)

Proposição 2.2.2.

(Erro da interpolação no espaço contínuo linear por partes.) O interpolador $\pi f\in V_{h}$ satisfaz as seguintes estimativas

	$\displaystyle\\|f-\pi f\\|_{L^{2}(\Omega)}^{2}\leq C\sum_{K\in\mathcal{K}}h_{K}^% {4}\\|D^{2}f\\|_{L^{2}(K)}^{2},$		(2.17)
	$\displaystyle\\|D(f-\pi f)\\|_{L^{2}(\Omega)}^{2}\leq C\sum_{K\in\mathcal{K}}h_{% K}^{2}\\|D^{2}f\\|_{L^{2}(K)}^{2},.$		(2.18)

Demonstração.

Demonstração análoga a Proposição 1.1.2. ∎

Observação 2.2.2.

(Taxa de convergência.) A taxa de convergência (ou ordem de truncamento) do erro de interpolação é definida como a potência do $h$ na estimativa (2.17). Esta taxa pode ser computacionalmente estimada. De fato, o erro de interpolação para uma dada malha $i$ tem a forma $\varepsilon_{i}\approx Ch_{i}^{r}$ . Conhecendo $\varepsilon_{i-1}\approx Ch_{i-1}^{r}$ para uma outra malha $i-1$ , podemos resolver para $r$ , obtendo a estimativa

r\approx\frac{\ln{\varepsilon_{i}/\varepsilon_{i-1}}}{\ln{h_{i}/h_{i-1}}}.

(2.19)

Exemplo 2.2.2.

Consideramos a interpolação feita no Exemplo 2.2.1. Aqui, computamos o erro de interpolação na norma $L^{2}$ , i.e.

\varepsilon=\|u_{h}-u\|_{L^{2}(\Omega)}

(2.20)

para diferentes refinamentos de malha.

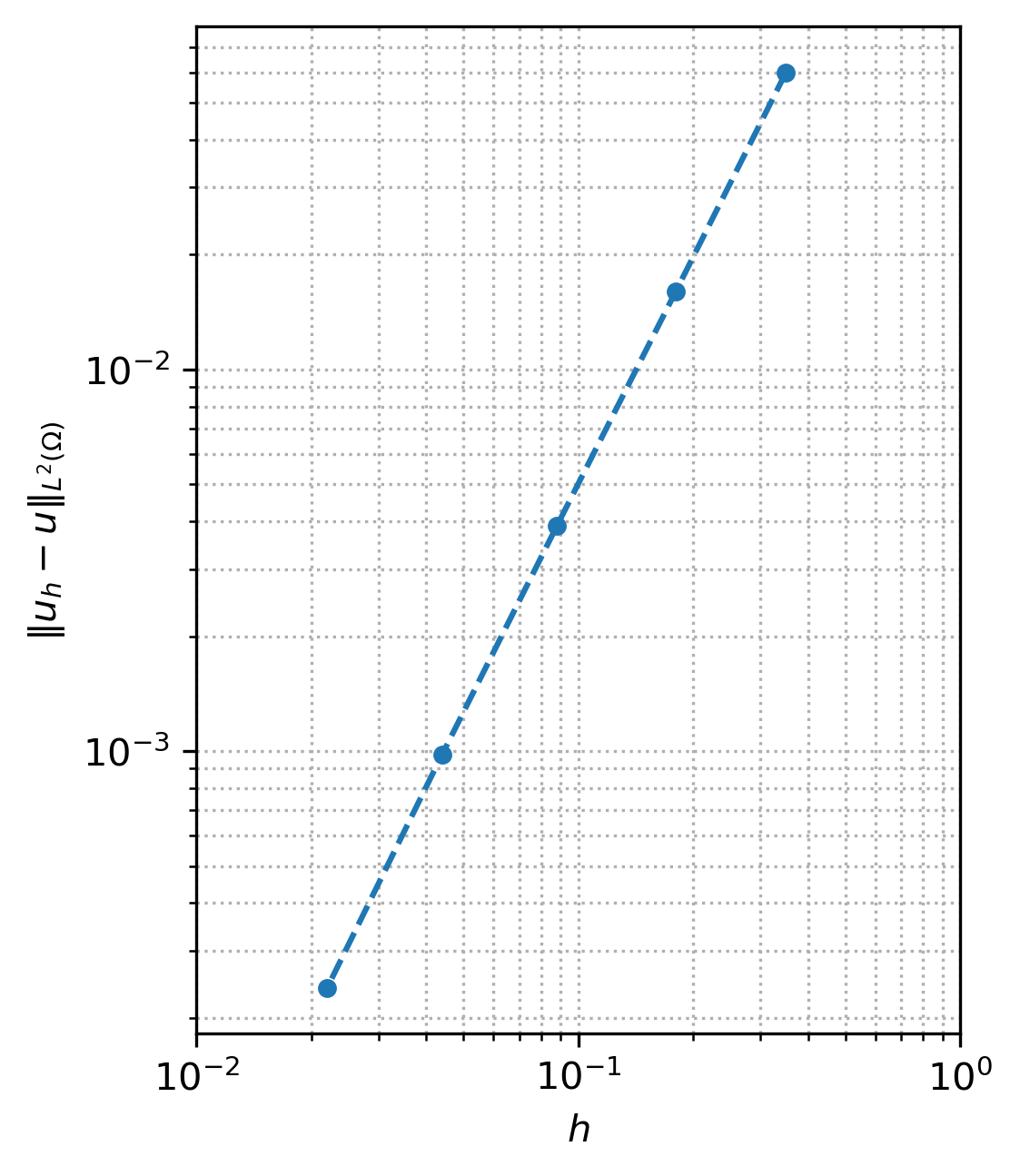
Na Tabela 2.1, temos o número de células e seu tamanho $h$ , o erro de interpolação $\varepsilon$ e a estimativa da taxa de convergência dada por (2.19).

Tabela 2.1: Erro de interpolação referente ao Exemplo 2.2.2.

#células	$h$	$\epsilon$	$r$
$4\times 4$	$3.5\times 10^{-1}$	$6.0\times 10^{-2}$	-x-
$8\times 8$	$1.8\times 10^{-1}$	$1.6\times 10^{-2}$	1.91
$16\times 16$	$8.8\times 10^{-2}$	$3.9\times 10^{-3}$	2.04
$32\times 32$	$4.4\times 10^{-2}$	$9.8\times 10^{-4}$	1.99
$64\times 64$	$2.2\times 10^{-2}$	$2.4e\times 10^{-4}$	2.03

2.2.1 Exercícios

Em construção

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Método de Elementos Finitos

2 Problemas Bidimensionais 2.1 Malha e Espaço 2.3 Projeção

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

2.2 Interpolação

Em revisão

Dada uma função contínua $f$ em um triângulo $K$ com nodos $N_{i}$ , $i=0,1,2$ , sua interpolação linear $\pi f\in P_{1}(K)$ é definida por

\pi f=\sum_{i=0}^{2}f(N_{i})\varphi_{i}.

(2.10)

Logo, temos $\pi f(N_{i})=f(N_{i})$ para todo $i=0,1,2$ .

Exemplo 2.2.1.

Consideramos a função

u(x_{0},x_{1})=\operatorname{sen}(\pi x_{0})\cos(\pi x_{1})

(2.11)

Código 9: interp2d.py

⬇

1from mpi4py import MPI

2from dolfinx import mesh

4# malha

5domain = mesh.create_unit_square(MPI.COMM_WORLD, 16, 16)

7from dolfinx import fem

9# espaço de elementos finitos

10V = fem.functionspace(domain, ("P",1))

12# função do espaço V

13uh = fem.Function(V)

15# interpolate

16import numpy as np

17def u(x, mod=np):

18 return mod.sin(mod.pi*x[0])*mod.sin(mod.pi*x[1])

20uh.interpolate(lambda x: u(x))

22# eval fun

23from dolfinx import geometry

25def fun_eval(u, points,

26 domain=domain):

27 u_values = []

28 bb_tree = geometry.bb_tree(domain, domain.topology.dim)

29 cells = []

30 points_on_proc = []

31 # Find cells whose bounding-box collide with the the points

32 cell_candidates = geometry.compute_collisions_points(bb_tree,

33 points.T)

34 # Choose one of the cells that contains the point

35 colliding_cells = geometry.compute_colliding_cells(domain,

36 cell_candidates,

37 points.T)

38 for i, point in enumerate(points.T):

39 if len(colliding_cells.links(i)) > 0:

40 points_on_proc.append(point)

41 cells.append(colliding_cells.links(i)[0])

43 points_on_proc = np.array(points_on_proc, dtype=np.float64)

44 u_values = u.eval(points_on_proc, cells)

45 return u_values

47# gráfico

48import numpy as np

49nx = ny = 101

50xx0 = np.linspace(0., 1., nx)

51xx1 = np.linspace(0., 1., ny)

52X0, X1 = np.meshgrid(xx0, xx1, indexing='ij')

53points = np.zeros((3, nx*ny))

54points[0] = X0.reshape(-1)

55points[1] = X1.reshape(-1)

57yh = fun_eval(uh, points)

58Yh = yh.reshape((nx,ny))

60import matplotlib.pyplot as plt

62fig = plt.figure()

63ax = fig.add_subplot()

64levels=10

65cb = ax.contourf(X0, X1, Yh, levels = levels)

66fig.colorbar(cb)

67Y = u([X0, X1])

68cl = ax.contour(X0, X1, Y, levels = levels, colors='w')

69ax.clabel(cl)

70plt.show()

Afim de determinarmos estimativas para o erro de interpolação, precisamos da chamada derivada total de primeira ordem

Df=\left(\left|\frac{\partial f}{\partial x_{0}}\right|^{2}+\left|\frac{% \partial f}{\partial x_{1}}\right|^{2}\right)^{1/2},

(2.12)

e da derivada total de segunda ordem

D^{2}f=\left(\left|\frac{\partial^{2}f}{\partial x_{0}^{2}}\right|^{2}+\left|% \frac{\partial^{2}f}{\partial x_{0}\partial x_{1}}\right|^{2}+\left|\frac{% \partial^{2}f}{\partial x_{1}^{2}}\right|^{2}\right)^{1/2}.

(2.13)

Proposição 2.2.1.

(Erro da interpolação no espaço linear.) A interpolação $\pi f$ satisfaz as seguintes estimativas

	$\displaystyle\\|f-\pi f\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}^{2}\\|D^{2}f\\|_{L^{2}(K)},$		(2.14)
	$\displaystyle\\|D(f-\pi f)\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}\\|D^{2}f\\|_{L^{2}(K)}.$		(2.15)

Demonstração.

Veja [1, Capítulo 4]. ∎

Observação 2.2.1.

A interpolação no espaço $V_{h}$ de uma dada função $f$ no domínio $\Omega$ é denotada também por $\pi f\in V_{h}$ e definida por

\pi f=\sum_{i=0}^{n_{p}-1}f(N_{i})\varphi_{i}.

(2.16)

Proposição 2.2.2.

(Erro da interpolação no espaço contínuo linear por partes.) O interpolador $\pi f\in V_{h}$ satisfaz as seguintes estimativas

	$\displaystyle\\|f-\pi f\\|_{L^{2}(\Omega)}^{2}\leq C\sum_{K\in\mathcal{K}}h_{K}^% {4}\\|D^{2}f\\|_{L^{2}(K)}^{2},$		(2.17)
	$\displaystyle\\|D(f-\pi f)\\|_{L^{2}(\Omega)}^{2}\leq C\sum_{K\in\mathcal{K}}h_{% K}^{2}\\|D^{2}f\\|_{L^{2}(K)}^{2},.$		(2.18)

Demonstração.

Demonstração análoga a Proposição 1.1.2. ∎

Observação 2.2.2.

r\approx\frac{\ln{\varepsilon_{i}/\varepsilon_{i-1}}}{\ln{h_{i}/h_{i-1}}}.

(2.19)

Exemplo 2.2.2.

Consideramos a interpolação feita no Exemplo 2.2.1. Aqui, computamos o erro de interpolação na norma $L^{2}$ , i.e.

\varepsilon=\|u_{h}-u\|_{L^{2}(\Omega)}

(2.20)

para diferentes refinamentos de malha.

Na Tabela 2.1, temos o número de células e seu tamanho $h$ , o erro de interpolação $\varepsilon$ e a estimativa da taxa de convergência dada por (2.19).

Tabela 2.1: Erro de interpolação referente ao Exemplo 2.2.2.

#células	$h$	$\epsilon$	$r$
$4\times 4$	$3.5\times 10^{-1}$	$6.0\times 10^{-2}$	-x-
$8\times 8$	$1.8\times 10^{-1}$	$1.6\times 10^{-2}$	1.91
$16\times 16$	$8.8\times 10^{-2}$	$3.9\times 10^{-3}$	2.04
$32\times 32$	$4.4\times 10^{-2}$	$9.8\times 10^{-4}$	1.99
$64\times 64$	$2.2\times 10^{-2}$	$2.4e\times 10^{-4}$	2.03

2.2.1 Exercícios

Em construção

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |

	$\displaystyle\\|f-\pi f\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}^{2}\\|D^{2}f\\|_{L^{2}(K)},$		(2.14)
	$\displaystyle\\|D(f-\pi f)\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}\\|D^{2}f\\|_{L^{2}(K)}.$		(2.15)

	$\displaystyle\\|f-\pi f\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}^{2}\\|D^{2}f\\|_{L^{2}(K)},$		(2.14)
	$\displaystyle\\|D(f-\pi f)\\|_{L^{2}(K)}$	$\displaystyle\leq Ch_{K}\\|D^{2}f\\|_{L^{2}(K)}.$		(2.15)