Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Método de Elementos Finitos
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.1 Malha e Espaço
Em revisão
2.1.1 Malha
Em revisão
Seja um domínio limitado com fronteira suave e poligonal. Uma malha (ou triangularização) de é um conjunto de células (ou elementos) , em que e tal que a interseção de duas células é ou um lado, um canto ou vazio.
Classicamente as células são escolhidas como triângulos. O comprimento do maior lado da célula define o chamado tamanho local da malha . O tamanho global da malha é definida por .
Uma malha é dita regular quando existe uma constante tal que para todo , sendo e o diâmetro do circulo inscrito em . Esta condição significa que os triângulos da malha não podem ter ângulos muito grandes nem muito pequenos. Ao longo do texto, a menos que especificado o contrário, assumiremos trabalhar com malhas regulares.
Exemplo 2.1.1.
O seguinte código, gera uma malha uniforme no domínio .

2.1.2 Espaço de Polinômios Lineares
Em revisão
Seja um triângulo e seja o espaço dos polinômios lineares em , i.e.
| (2.1) | ||||
Observamos que toda função é unicamente determinada por seus valores nodais
| (2.2) |
onde é o -ésimo nodo (vértice) do triângulo . Isto segue do fato de que o sistema (2.2) tem forma matricial
| (2.3) |
Ainda, o valor absoluto do determinante da matriz de coeficientes é , onde denota a área de , a qual é não nula.
Afim de usarmos os valores nodais como graus de liberdade (incógnitas), nós introduzimos a seguinte base nodal com
| (2.4) |
Com esta base, toda função pode ser escrita como
| (2.5) |
onde .
2.1.3 Espaço contínuo dos polinômios lineares por partes
Em revisão
O espaço contínuo dos polinômios lineares por partes na malha é definido por
| (2.6) |
Observamos que toda função é unicamente determinada por seus valores nodais , onde é número de nodos da malha .
De fato, os valores nodais determinam uma única função em para cada e, portanto, uma função em é unicamente determinada por seus valores nos nodos. Agora, consideremos dois triângulos e compartilhando um lado . Sejam e os dois únicos polinômios em e , respectivamente determinados pelos valores nodais em e . Como e também são polinômios lineares em e seus valores coincidem nos nodos de , temos em . Portanto, concluímos que toda função é unicamente determinada por seus valores nodais.
Afim de termos os valores nodais como graus de liberdade (incógnitas), definimos a base nodal tal que
| (2.7) |
Notamos que cada função base é contínua, polinômio linear por partes e com suporte somente em um pequeno conjunto de triângulos que compartilham o nodo . Além disso, toda a função pode, então, ser escrita como
| (2.8) |
onde , , são os valores nodais de .
Exemplo 2.1.2.
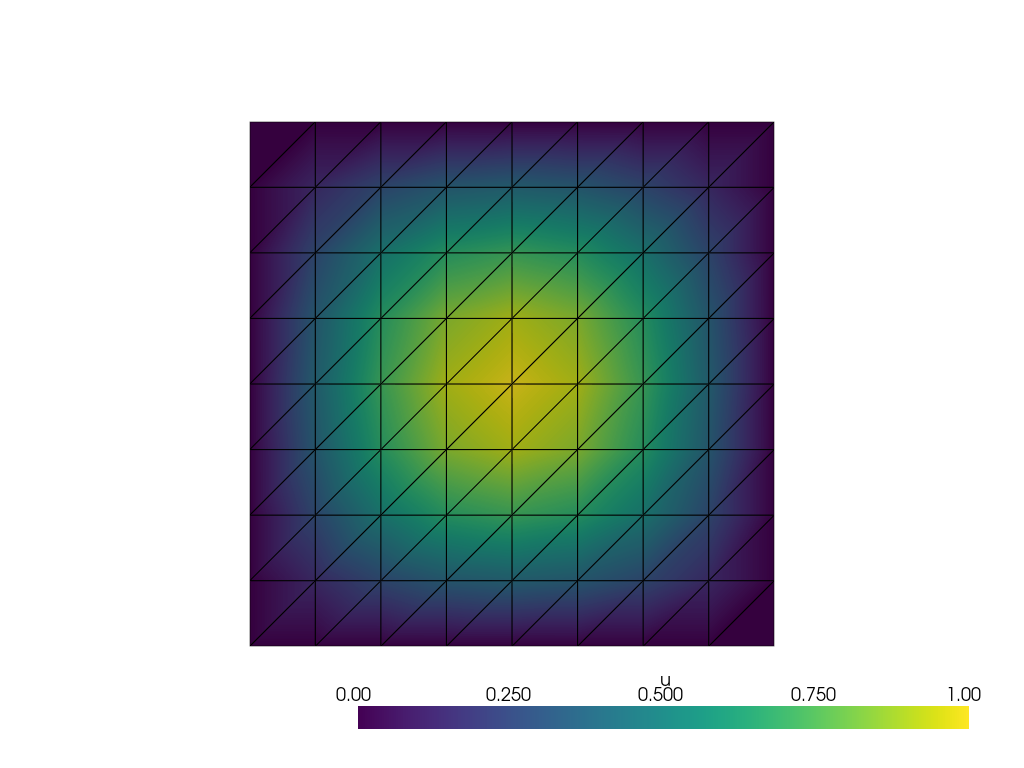
No seguinte código, alocamos um espaço de elementos finitos sobre uma malha regular no domínio . Ainda, uma função é alocada com valores nodais
| (2.9) |
2.1.4 Exercícios
Em construção
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Método de Elementos Finitos
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
2.1 Malha e Espaço
Em revisão
2.1.1 Malha
Em revisão
Seja um domínio limitado com fronteira suave e poligonal. Uma malha (ou triangularização) de é um conjunto de células (ou elementos) , em que e tal que a interseção de duas células é ou um lado, um canto ou vazio.
Classicamente as células são escolhidas como triângulos. O comprimento do maior lado da célula define o chamado tamanho local da malha . O tamanho global da malha é definida por .
Uma malha é dita regular quando existe uma constante tal que para todo , sendo e o diâmetro do circulo inscrito em . Esta condição significa que os triângulos da malha não podem ter ângulos muito grandes nem muito pequenos. Ao longo do texto, a menos que especificado o contrário, assumiremos trabalhar com malhas regulares.
Exemplo 2.1.1.
O seguinte código, gera uma malha uniforme no domínio .

2.1.2 Espaço de Polinômios Lineares
Em revisão
Seja um triângulo e seja o espaço dos polinômios lineares em , i.e.
| (2.1) | ||||
Observamos que toda função é unicamente determinada por seus valores nodais
| (2.2) |
onde é o -ésimo nodo (vértice) do triângulo . Isto segue do fato de que o sistema (2.2) tem forma matricial
| (2.3) |
Ainda, o valor absoluto do determinante da matriz de coeficientes é , onde denota a área de , a qual é não nula.
Afim de usarmos os valores nodais como graus de liberdade (incógnitas), nós introduzimos a seguinte base nodal com
| (2.4) |
Com esta base, toda função pode ser escrita como
| (2.5) |
onde .
2.1.3 Espaço contínuo dos polinômios lineares por partes
Em revisão
O espaço contínuo dos polinômios lineares por partes na malha é definido por
| (2.6) |
Observamos que toda função é unicamente determinada por seus valores nodais , onde é número de nodos da malha .
De fato, os valores nodais determinam uma única função em para cada e, portanto, uma função em é unicamente determinada por seus valores nos nodos. Agora, consideremos dois triângulos e compartilhando um lado . Sejam e os dois únicos polinômios em e , respectivamente determinados pelos valores nodais em e . Como e também são polinômios lineares em e seus valores coincidem nos nodos de , temos em . Portanto, concluímos que toda função é unicamente determinada por seus valores nodais.
Afim de termos os valores nodais como graus de liberdade (incógnitas), definimos a base nodal tal que
| (2.7) |
Notamos que cada função base é contínua, polinômio linear por partes e com suporte somente em um pequeno conjunto de triângulos que compartilham o nodo . Além disso, toda a função pode, então, ser escrita como
| (2.8) |
onde , , são os valores nodais de .
Exemplo 2.1.2.
No seguinte código, alocamos um espaço de elementos finitos sobre uma malha regular no domínio . Ainda, uma função é alocada com valores nodais
| (2.9) |

2.1.4 Exercícios
Em construção
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.