Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Método de Elementos Finitos
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.1 Interpolação e Projeção
Em revisão
Seja dado um intervalo , . O espaço vetorial das funções lineares em é definido por
| (1.1) |
Observamos que dado , temos que é unicamente determinada pelos valores
| (1.2) | ||||
Como consequência, existe exatamente uma única função para quaisquer dados valores e . Desta observação, introduzimos a chamada base nodal (base lagrangiana11endnote: 1Consulte mais em Notas de Aula: Matemática Numérica I: Interpolação de Lagrange.) para , definida por
| (1.3) |
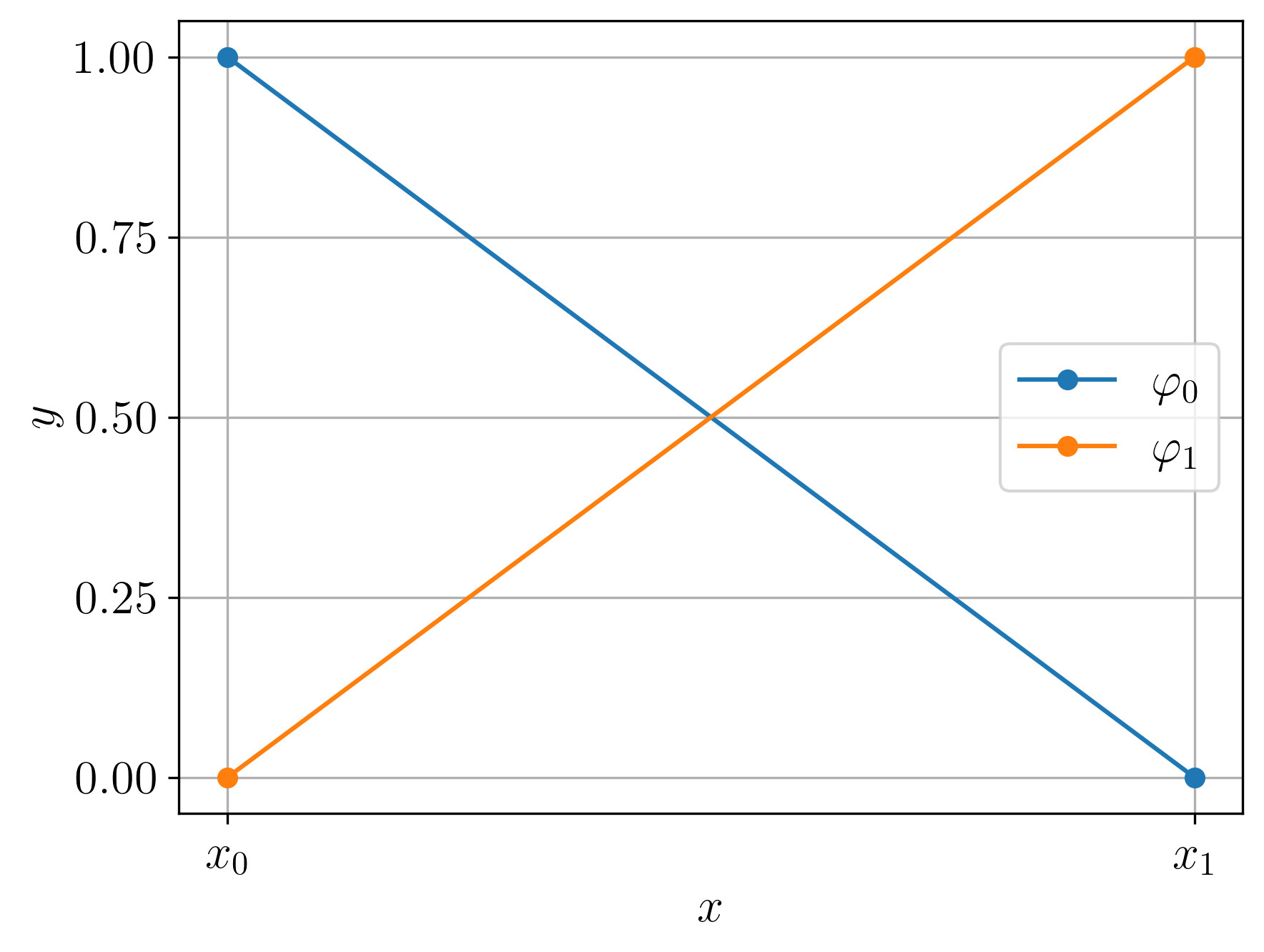
com . Consulte a Figura 1.1.
Com esta base, toda função pode ser escrita como uma combinação linear das funções e com coeficientes e (graus de liberdade), i.e.
| (1.4) |
Além disso, observamos que
| (1.5) | |||
| (1.6) |
Uma extensão do espaço é o espaço das funções lineares por partes. Dado , , consideramos uma partição (malha) de com pontos
| (1.7) |
e, portanto, com subintervalos de comprimento (tamanho da malha) , . Na malha definimos o seguinte espaço das funções lineares por partes
| (1.8) |
Observamos que toda função é unicamente determinada por seus valores nodais . Reciprocamente, todo conjunto de valores nodas determina unicamente uma função . Desta observação, temos que os valores nodais determinam os graus de liberdade com a base nodal para definida por
| (1.9) |
com . Ou seja, temos que
| (1.10) |
Podemos verificar que
| (1.11) |
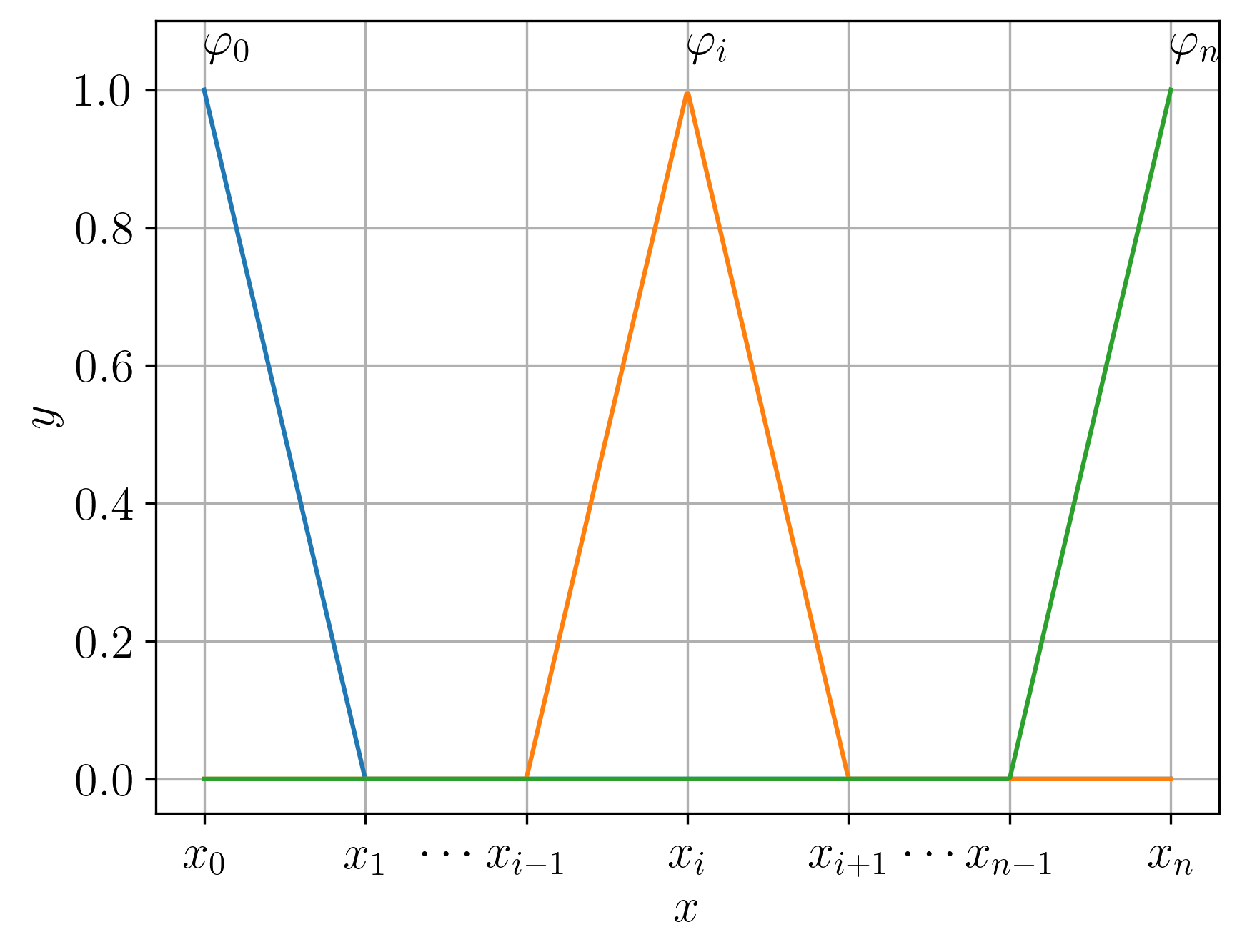
consulte, Figura 1.2. É notável que tem suporte compacto .
1.1.1 Interpolação
Em revisão
Interpolação é uma técnica de aproximação de funções. Dada uma função contínua em , definimos o operador de interpolação linear por
| (1.12) |
Observamos que é igual a nos nodos , .
Exemplo 1.1.1.
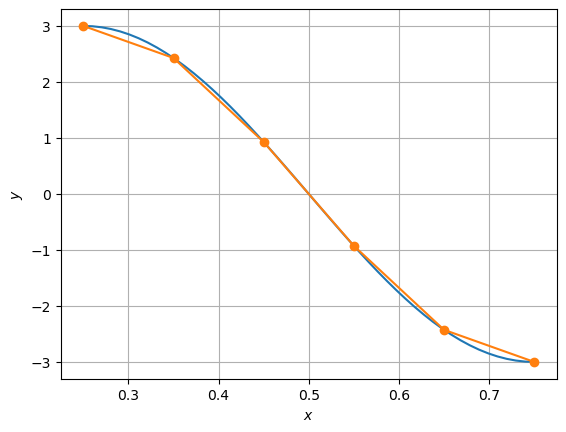
A Figura 1.3 ilustra a interpolação da função no espaço de elementos finitos das funções lineares por partes com células.
Agora, vamos buscar medir o erro de interpolação, i.e. . Para tanto, podemos usar a norma definida por
| (1.13) |
Lembramos que valem a desigualdade triangular
| (1.14) |
e a desigualdade de Cauchy-Schwarz22endnote: 2Também conhecida como desigualdade de Cauchy–Bunyakovsky–Schwarz. Augustin-Louis Cauchy, 1789 - 1857, matemático francês. Viktor Yakovlevich Bunyakovsky, 1804 - 1889, matemático Russo. Karl Hermann Amandus Schwarz, 1843 - 1921, matemático alemão.
| (1.15) |
para qualquer funções .
Proposição 1.1.1.
(Erro da interpolação linear) O interpolador satisfaz as estimativas
| (1.16) | ||||
| (1.17) |
onde é uma constante e .
Demonstração.
Denotemos o erro de interpolação por . Do teorema fundamental do cálculo, temos
| (1.18) |
onde . Daí, usando a desigualdade de Cauchy-Schwarz (1.15), temos
| (1.19) | ||||
| (1.20) | ||||
| (1.21) | ||||
| (1.22) | ||||
| (1.23) |
donde
| (1.24) |
Então, integrando em obtemos
| (1.25) |
ou seja, temos a seguinte desigualdade
| (1.26) |
Agora, observando que , o teorema de Rolle33endnote: 3Michel Rolle, 1652 - 1719, matemático francês. garante a existência de um ponto tal que , donde do teorema fundamental do cálculo e da desigualdade de Cauchy-Schwarz, segue
| (1.27) | ||||
| (1.28) | ||||
| (1.29) | ||||
| (1.30) |
Então, integrando em , obtemos
| (1.31) |
a qual, observando que , equivale a segunda estimativa procurada, i.e.
| (1.32) |
Por fim, de (1.31) e de (1.26), obtemos a primeira estimativa desejada
| (1.33) |
∎
Vamos, agora, generalizar o resultado da Proposição 1.1.1 para a interpolação no espaço das funções lineares por parte.
O seguinte resultado fornece uma estimativa do erro de interpolação em relação ao tamanho de cada elemento da malha.
Proposição 1.1.2.
O interpolador satisfaz as estimativas
| (1.34) | ||||
| (1.35) |
Demonstração.
Ambas desigualdades seguem da desigualdade triangular e da Proposição 1.1.1. Por exemplo, para a primeira desigualdade, temos
| (1.37) | ||||
| (1.38) |
∎
1.1.2 Projeção
Em revisão
Dada uma função , definimos o operador de projeção por
| (1.39) |
Como é um espaço de dimensão finita, a condição (1.39) é equivalente a
| (1.40) |
onde é a -ésima função base de . Além disso, como , temos
| (1.41) |
onde , , são incógnitas a determinar. Logo,
| (1.42) | |||
| (1.43) | |||
| (1.44) | |||
| (1.45) |
para .
Observamos que (1.45) consiste em um sistema de equações lineares para as incógnitas , . Este, por sua vez, pode ser escrito na seguinte forma matricial
| (1.46) |
onde é chamada de matriz de massa
| (1.47) |
e é chamado de vetor de carregamento
| (1.48) |
Exemplo 1.1.2.
A Figura 1.4 ilustra a projeção da função no espaço das funções lineares por partes em uma malha uniforme do intervalo com subintervalos ( células).

O próximo teorema mostra que é a função que melhor aproxima dentre todas as funções do espaço .
Teorema 1.1.1.
(A melhor aproximação.) A projeção satisfaz
| (1.50) |
Demonstração.
Dado , temos
| (1.51) | ||||
| (1.52) | ||||
| (1.53) | ||||
| (1.54) | ||||
| (1.55) |
donde segue o resultado. ∎
O próximo teorema fornece uma estimativa a-priori do erro em relação ao tamanho da malha.
Teorema 1.1.2.
A projeção satisfaz
| (1.56) |
1.1.3 Exercícios
Em revisão
E. 1.1.1.
Faça um código para verificar a segunda estimativa da Proposição 1.1.1 no caso da interpolação da função no espaço das funções lineares.
Resposta 0.
badgeConstrucao
E. 1.1.2.
Faça um código para verificar as estimativas da Proposição 1.1.2 no caso da interpolação da função no espaço das funções lineares por partes.
E. 1.1.3.
Faça um código para computar a projeção da função no espaço das funções lineares por partes em uma malha com células no intervalo . Faça o esboço dos gráficos de e e compute o erro .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Método de Elementos Finitos
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.1 Interpolação e Projeção
Em revisão
Seja dado um intervalo , . O espaço vetorial das funções lineares em é definido por
| (1.1) |
Observamos que dado , temos que é unicamente determinada pelos valores
| (1.2) | ||||
Como consequência, existe exatamente uma única função para quaisquer dados valores e . Desta observação, introduzimos a chamada base nodal (base lagrangiana11endnote: 1Consulte mais em Notas de Aula: Matemática Numérica I: Interpolação de Lagrange.) para , definida por
| (1.3) |
com . Consulte a Figura 1.1.

Com esta base, toda função pode ser escrita como uma combinação linear das funções e com coeficientes e (graus de liberdade), i.e.
| (1.4) |
Além disso, observamos que
| (1.5) | |||
| (1.6) |
Uma extensão do espaço é o espaço das funções lineares por partes. Dado , , consideramos uma partição (malha) de com pontos
| (1.7) |
e, portanto, com subintervalos de comprimento (tamanho da malha) , . Na malha definimos o seguinte espaço das funções lineares por partes
| (1.8) |
Observamos que toda função é unicamente determinada por seus valores nodais . Reciprocamente, todo conjunto de valores nodas determina unicamente uma função . Desta observação, temos que os valores nodais determinam os graus de liberdade com a base nodal para definida por
| (1.9) |
com . Ou seja, temos que
| (1.10) |
Podemos verificar que
| (1.11) |
consulte, Figura 1.2. É notável que tem suporte compacto .

1.1.1 Interpolação
Em revisão
Interpolação é uma técnica de aproximação de funções. Dada uma função contínua em , definimos o operador de interpolação linear por
| (1.12) |
Observamos que é igual a nos nodos , .
Exemplo 1.1.1.
A Figura 1.3 ilustra a interpolação da função no espaço de elementos finitos das funções lineares por partes com células.

Agora, vamos buscar medir o erro de interpolação, i.e. . Para tanto, podemos usar a norma definida por
| (1.13) |
Lembramos que valem a desigualdade triangular
| (1.14) |
e a desigualdade de Cauchy-Schwarz22endnote: 2Também conhecida como desigualdade de Cauchy–Bunyakovsky–Schwarz. Augustin-Louis Cauchy, 1789 - 1857, matemático francês. Viktor Yakovlevich Bunyakovsky, 1804 - 1889, matemático Russo. Karl Hermann Amandus Schwarz, 1843 - 1921, matemático alemão.
| (1.15) |
para qualquer funções .
Proposição 1.1.1.
(Erro da interpolação linear) O interpolador satisfaz as estimativas
| (1.16) | ||||
| (1.17) |
onde é uma constante e .
Demonstração.
Denotemos o erro de interpolação por . Do teorema fundamental do cálculo, temos
| (1.18) |
onde . Daí, usando a desigualdade de Cauchy-Schwarz (1.15), temos
| (1.19) | ||||
| (1.20) | ||||
| (1.21) | ||||
| (1.22) | ||||
| (1.23) |
donde
| (1.24) |
Então, integrando em obtemos
| (1.25) |
ou seja, temos a seguinte desigualdade
| (1.26) |
Agora, observando que , o teorema de Rolle33endnote: 3Michel Rolle, 1652 - 1719, matemático francês. garante a existência de um ponto tal que , donde do teorema fundamental do cálculo e da desigualdade de Cauchy-Schwarz, segue
| (1.27) | ||||
| (1.28) | ||||
| (1.29) | ||||
| (1.30) |
Então, integrando em , obtemos
| (1.31) |
a qual, observando que , equivale a segunda estimativa procurada, i.e.
| (1.32) |
Por fim, de (1.31) e de (1.26), obtemos a primeira estimativa desejada
| (1.33) |
∎
Vamos, agora, generalizar o resultado da Proposição 1.1.1 para a interpolação no espaço das funções lineares por parte.
O seguinte resultado fornece uma estimativa do erro de interpolação em relação ao tamanho de cada elemento da malha.
Proposição 1.1.2.
O interpolador satisfaz as estimativas
| (1.34) | ||||
| (1.35) |
Demonstração.
Ambas desigualdades seguem da desigualdade triangular e da Proposição 1.1.1. Por exemplo, para a primeira desigualdade, temos
| (1.37) | ||||
| (1.38) |
∎
1.1.2 Projeção
Em revisão
Dada uma função , definimos o operador de projeção por
| (1.39) |
Como é um espaço de dimensão finita, a condição (1.39) é equivalente a
| (1.40) |
onde é a -ésima função base de . Além disso, como , temos
| (1.41) |
onde , , são incógnitas a determinar. Logo,
| (1.42) | |||
| (1.43) | |||
| (1.44) | |||
| (1.45) |
para .
Observamos que (1.45) consiste em um sistema de equações lineares para as incógnitas , . Este, por sua vez, pode ser escrito na seguinte forma matricial
| (1.46) |
onde é chamada de matriz de massa
| (1.47) |
e é chamado de vetor de carregamento
| (1.48) |
Exemplo 1.1.2.
A Figura 1.4 ilustra a projeção da função no espaço das funções lineares por partes em uma malha uniforme do intervalo com subintervalos ( células).

O próximo teorema mostra que é a função que melhor aproxima dentre todas as funções do espaço .
Teorema 1.1.1.
(A melhor aproximação.) A projeção satisfaz
| (1.50) |
Demonstração.
Dado , temos
| (1.51) | ||||
| (1.52) | ||||
| (1.53) | ||||
| (1.54) | ||||
| (1.55) |
donde segue o resultado. ∎
O próximo teorema fornece uma estimativa a-priori do erro em relação ao tamanho da malha.
Teorema 1.1.2.
A projeção satisfaz
| (1.56) |
1.1.3 Exercícios
Em revisão
E. 1.1.1.
Faça um código para verificar a segunda estimativa da Proposição 1.1.1 no caso da interpolação da função no espaço das funções lineares.
Resposta 0.
badgeConstrucao
E. 1.1.2.
Faça um código para verificar as estimativas da Proposição 1.1.2 no caso da interpolação da função no espaço das funções lineares por partes.
E. 1.1.3.
Faça um código para computar a projeção da função no espaço das funções lineares por partes em uma malha com células no intervalo . Faça o esboço dos gráficos de e e compute o erro .
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.