Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Geometria Analítica
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
4.1 Introdução a superfícies quádricas
Superfícies no espaço que podem ser descritas por equações da forma
| (4.1) |
são chamadas de superfícies quádricas, sendo , , , , , , , , e coeficientes dados.
4.1.1 Elipsoides
Um elipsoide centrado na origem é uma superfície quádrica de equação
| (4.2) |
Exemplo 4.1.1.
A Figura 4.1 é um esboço do gráfico da elipsoide de equação
| (4.3) |
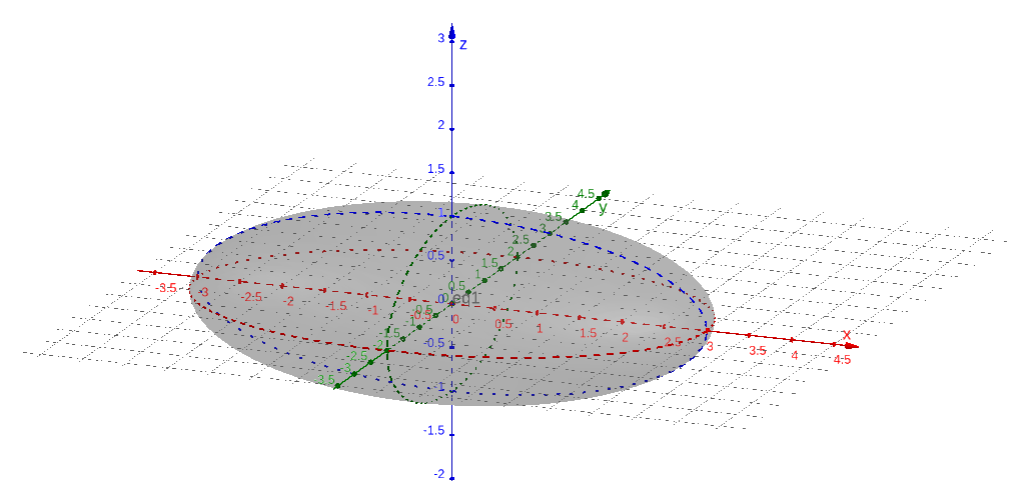
Observamos que a interseção deste elipsoide com o plano (z=0) é a elipse de equação
| (4.4) |
Ou seja, é a elipse de vértice sobre o eixo maior e e vértices sobre o eixo menor e .
4.1.2 Hiperboloides
Hiperboloides de uma folha
Um hiperboloide de uma folha centrado na origem é uma superfície quádrica de equação
| (4.7) |
ou
| (4.8) |
ou
| (4.9) |
Exemplo 4.1.2.
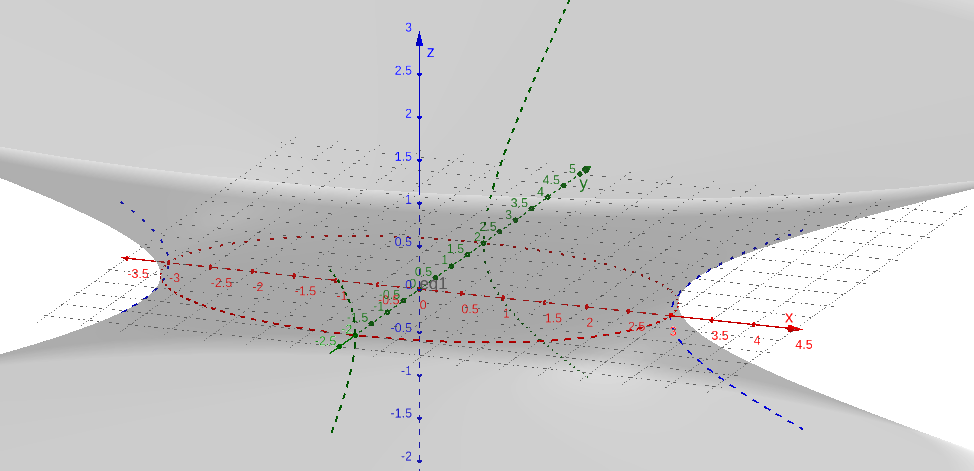
Vamos considerar o hiperboloide de equação
| (4.10) |
Sua interseção com o plano () é a elipse
| (4.11) |
Sua interseção com o plano (y=0) é a hipérbole de equação reduzida
| (4.12) |
E, a interseção do hiperboloide com o plano () é a hipérbole de equação
| (4.13) |
Exemplo 4.1.3.
A Figura 4.3 é o esboço do gráfico do hiperboloide de equação
| (4.14) |
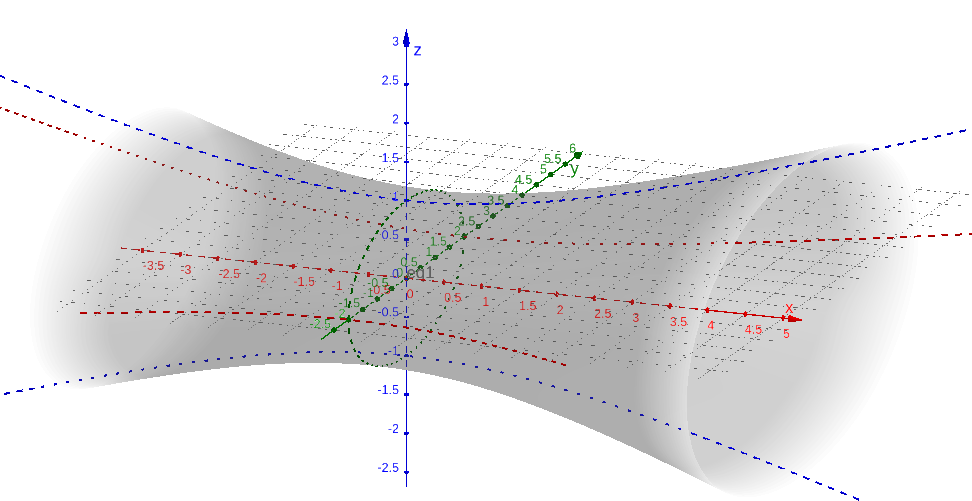
Sua interseção com o plano () é a hipérbole
| (4.15) |
Sua interseção com o plano (y=0) é a hipérbole de equação reduzida
| (4.16) |
E, a interseção do hiperboloide com o plano () é a elipse de equação
| (4.17) |
Hiperboloides de duas folhas
Hiperboloides de duas folhas têm equações
| (4.18) |
ou
| (4.19) |
ou
| (4.20) |
Exemplo 4.1.4.
Vamos considerar o hiperboloide de equação
| (4.21) |
Sua interseção com o plano () é a hipérbole
| (4.22) |
Sua interseção com o plano (y=0) é a hipérbole de equação reduzida
| (4.23) |
E, a interseção do hiperboloide com o plano () é vazia, pois não existem e que satisfazem a equação
| (4.24) |

4.1.3 Paraboloide elíptico
Um paraboloide elíptico tem equação
| (4.25) |
ou
| (4.26) |
ou
| (4.27) |
Exemplo 4.1.5.
Vamos considerar o paraboloide elíptico de equação
| (4.28) |
Não há valor que satisfaça a equação (4.28). Sua interseção com o plano () é o ponto . Agora, sua interseção com cada plano paralelo ao plano e com é a elipse de equação
| (4.29) |
ou, equivalentemente,
| (4.30) |

4.1.4 Paraboloide hiperbólico
Um paraboloide elíptico tem equação
| (4.32) |
ou
| (4.33) |
ou
| (4.34) |
Exemplo 4.1.7.
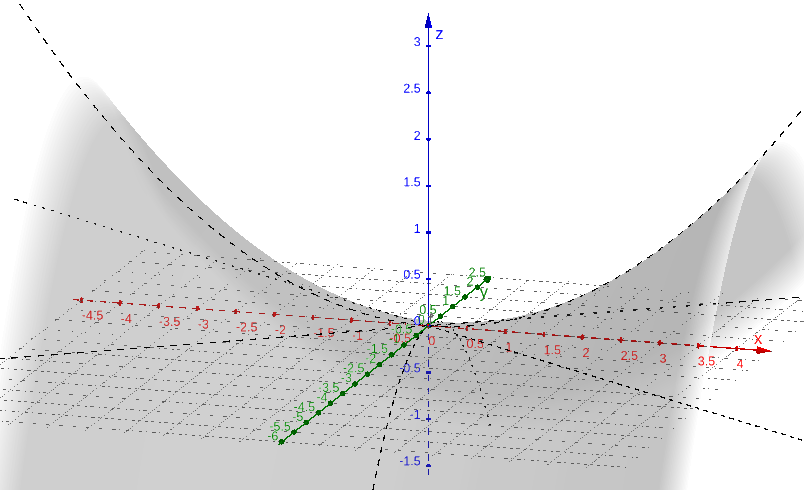
Vamos considerar o paraboloide hiperbólico de equação
| (4.35) |
Sua interseção com o plano () são retas que satisfazem a equação
| (4.36) |
De fato, isolando , obtemos as equações destas retas
| (4.37) |
Sua interseção com o plano (y=0) é a parábola de equação
| (4.38) |
E, a interseção do paraboloide hiperbólico com o plano () é a parábola de equação
| (4.39) |
Exercícios resolvidos
ER 4.1.1.
Escreva a equação do elipsoide que tem como interseções
-
a)
com o plano a elipse
(4.40) -
b)
com o plano a elipse
(4.41)
Solução 0.
Um elipsoide tem equação
| (4.42) |
Sua interseção com o plano () é a elipse de equação
| (4.43) |
Logo, do item a), temos e .
Agora, a interseção com o plano () é a elipse de equação
| (4.44) |
Assim, do item b), obtemos .
Desta forma, concluímos que o elipsoide de equação
| (4.45) |
ER 4.1.2.
Encontre a equação do paraboloide elíptico que contem a circunferência
| (4.46) |
Solução 0.
Para que o paraboloide contenha a circunferência
| (4.47) |
ele precisa abrir-se no sentido negativo na direção . Logo, tem equação
| (4.48) |
Fixado , a equação fica restrita a
| (4.49) |
Notamos que para esta equação coincida com a circunferência , devemos escolher . Logo, concluímos que o paraboloide elíptico tem equação
| (4.50) |
Exercícios
E. 4.1.1.
Classifique cada uma das seguintes superfícies quádricas:
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) hiperboloide de uma folha; b) elipsoide; c) paraboloide elíptico; d) ponto
E. 4.1.2.
Forneça a equação do elipsoide que contem os pontos , e .
Resposta 0.
E. 4.1.3.
Forneça a equação do hiperboloide de duas folhas que tem interseções:
-
a)
com o eixo igual a hipérbole
(4.51) -
b)
com o eixo igual a hipérbole
(4.52)
Resposta 0.
E. 4.1.4.
Forneça a equação do paraboloide elíptico que contem a elipse
| (4.53) |
Resposta 0.
E. 4.1.5.
Considere o hiperboloide de uma folha de equação
| (4.54) |
Classifique o lugar geométrico de sua interseção com cada um dos seguintes planos
-
1.
-
2.
-
3.
Resposta 0.
a) hipérbole; b) elipse; c) hipérbole
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Geometria Analítica
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
4.1 Introdução a superfícies quádricas
Superfícies no espaço que podem ser descritas por equações da forma
| (4.1) |
são chamadas de superfícies quádricas, sendo , , , , , , , , e coeficientes dados.
4.1.1 Elipsoides
Um elipsoide centrado na origem é uma superfície quádrica de equação
| (4.2) |
Exemplo 4.1.1.
A Figura 4.1 é um esboço do gráfico da elipsoide de equação
| (4.3) |

Observamos que a interseção deste elipsoide com o plano (z=0) é a elipse de equação
| (4.4) |
Ou seja, é a elipse de vértice sobre o eixo maior e e vértices sobre o eixo menor e .
4.1.2 Hiperboloides
Hiperboloides de uma folha
Um hiperboloide de uma folha centrado na origem é uma superfície quádrica de equação
| (4.7) |
ou
| (4.8) |
ou
| (4.9) |
Exemplo 4.1.2.
Vamos considerar o hiperboloide de equação
| (4.10) |
Sua interseção com o plano () é a elipse
| (4.11) |
Sua interseção com o plano (y=0) é a hipérbole de equação reduzida
| (4.12) |
E, a interseção do hiperboloide com o plano () é a hipérbole de equação
| (4.13) |

Exemplo 4.1.3.
A Figura 4.3 é o esboço do gráfico do hiperboloide de equação
| (4.14) |

Sua interseção com o plano () é a hipérbole
| (4.15) |
Sua interseção com o plano (y=0) é a hipérbole de equação reduzida
| (4.16) |
E, a interseção do hiperboloide com o plano () é a elipse de equação
| (4.17) |
Hiperboloides de duas folhas
Hiperboloides de duas folhas têm equações
| (4.18) |
ou
| (4.19) |
ou
| (4.20) |
Exemplo 4.1.4.
Vamos considerar o hiperboloide de equação
| (4.21) |
Sua interseção com o plano () é a hipérbole
| (4.22) |
Sua interseção com o plano (y=0) é a hipérbole de equação reduzida
| (4.23) |
E, a interseção do hiperboloide com o plano () é vazia, pois não existem e que satisfazem a equação
| (4.24) |

4.1.3 Paraboloide elíptico
Um paraboloide elíptico tem equação
| (4.25) |
ou
| (4.26) |
ou
| (4.27) |
Exemplo 4.1.5.
Vamos considerar o paraboloide elíptico de equação
| (4.28) |
Não há valor que satisfaça a equação (4.28). Sua interseção com o plano () é o ponto . Agora, sua interseção com cada plano paralelo ao plano e com é a elipse de equação
| (4.29) |
ou, equivalentemente,
| (4.30) |

4.1.4 Paraboloide hiperbólico
Um paraboloide elíptico tem equação
| (4.32) |
ou
| (4.33) |
ou
| (4.34) |
Exemplo 4.1.7.
Vamos considerar o paraboloide hiperbólico de equação
| (4.35) |
Sua interseção com o plano () são retas que satisfazem a equação
| (4.36) |
De fato, isolando , obtemos as equações destas retas
| (4.37) |
Sua interseção com o plano (y=0) é a parábola de equação
| (4.38) |
E, a interseção do paraboloide hiperbólico com o plano () é a parábola de equação
| (4.39) |

Exercícios resolvidos
ER 4.1.1.
Escreva a equação do elipsoide que tem como interseções
-
a)
com o plano a elipse
(4.40) -
b)
com o plano a elipse
(4.41)
Solução 0.
Um elipsoide tem equação
| (4.42) |
Sua interseção com o plano () é a elipse de equação
| (4.43) |
Logo, do item a), temos e .
Agora, a interseção com o plano () é a elipse de equação
| (4.44) |
Assim, do item b), obtemos .
Desta forma, concluímos que o elipsoide de equação
| (4.45) |
ER 4.1.2.
Encontre a equação do paraboloide elíptico que contem a circunferência
| (4.46) |
Solução 0.
Para que o paraboloide contenha a circunferência
| (4.47) |
ele precisa abrir-se no sentido negativo na direção . Logo, tem equação
| (4.48) |
Fixado , a equação fica restrita a
| (4.49) |
Notamos que para esta equação coincida com a circunferência , devemos escolher . Logo, concluímos que o paraboloide elíptico tem equação
| (4.50) |
Exercícios
E. 4.1.1.
Classifique cada uma das seguintes superfícies quádricas:
-
a)
-
b)
-
c)
-
d)
Resposta 0.
a) hiperboloide de uma folha; b) elipsoide; c) paraboloide elíptico; d) ponto
E. 4.1.2.
Forneça a equação do elipsoide que contem os pontos , e .
Resposta 0.
E. 4.1.3.
Forneça a equação do hiperboloide de duas folhas que tem interseções:
-
a)
com o eixo igual a hipérbole
(4.51) -
b)
com o eixo igual a hipérbole
(4.52)
Resposta 0.
E. 4.1.4.
Forneça a equação do paraboloide elíptico que contem a elipse
| (4.53) |
Resposta 0.
E. 4.1.5.
Considere o hiperboloide de uma folha de equação
| (4.54) |
Classifique o lugar geométrico de sua interseção com cada um dos seguintes planos
-
1.
-
2.
-
3.
Resposta 0.
a) hipérbole; b) elipse; c) hipérbole
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
