Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Política de uso de dados
Ao navegar por este site, você concorda com a política de uso de dados.Geometria Analítica
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.3 Equações do plano
Em revisão
Um plano fica unicamente determinado por um ponto e dois vetores linearmente independentes 22endnote: 2No sentido que e têm representantes no plano .. Veja a Figura 1.9.
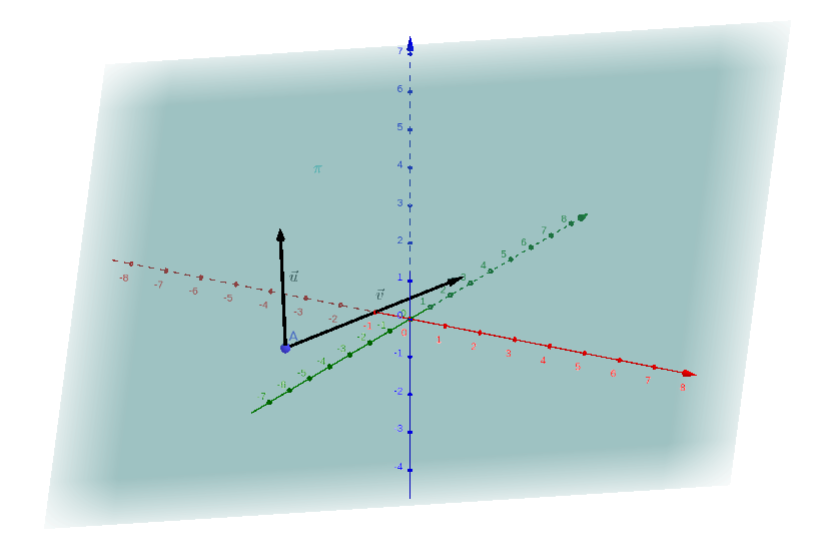
Os chamados vetores diretores e determinam infinitos planos paralelos entre si. O chamado ponto de ancoragem fixa um destes planos.
1.3.1 Equação vetorial do plano
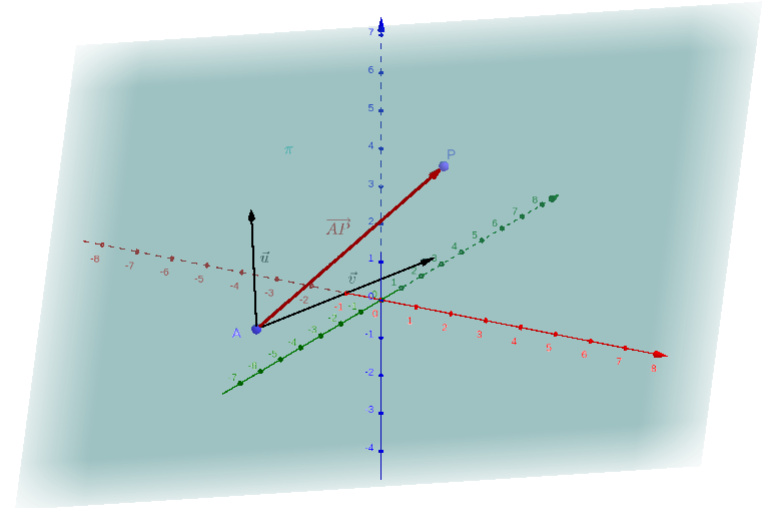
Consideremos um plano determinado pelo ponto de ancoragem e os vetores diretores e (veja a Figura 1.10). Então, um ponto se, e somente se, é coplanar a e , i.e. , e são linearmente dependentes. Ou seja, se, e somente se, pode ser escrito como combinação linear de e . Isto nos fornece a chamada equação vetorial do plano
| (1.94) |
Exemplo 1.3.1.
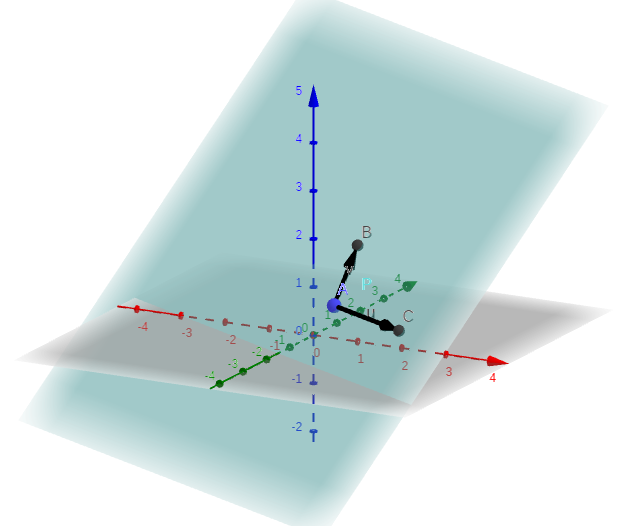
Consideremos o plano determinado pelo ponto e pelos vetores e (Veja a Figura 1.11. Desta forma, uma equação vetorial para este plano é
| (1.95) |
para .
Tomando, por exemplo, e , obtemos
| (1.96) | ||||
| (1.97) | ||||
| (1.98) |
Observando que as coordenadas do ponto são iguais as coordenadas do vetor , temos
| (1.99) | ||||
| (1.100) | ||||
| (1.101) |
Ou seja, .
1.3.2 Equações paramétricas do plano
Seja um plano com ponto de ancoragem e vetores diretores e . Então, todo o ponto neste plano satisfaz a equação vetorial
| (1.102) |
para dados parâmetros . Assim, temos
| (1.103) | ||||
| (1.104) |
Portanto, temos
| (1.105) | ||||
| (1.106) | ||||
| (1.107) |
Ou, equivalentemente,
| (1.108) | ||||
| (1.109) | ||||
| (1.110) |
as quais são chamadas de equações paramétricas do plano.
Exemplo 1.3.2.
No Exemplo 1.3.1, discutimos sobre o plano determinado pelo ponto e os vetores e . Do que vimos acima, temos que
| (1.111) | ||||
| (1.112) | ||||
| (1.113) |
são equações paramétricas deste plano.
Podemos usar as equações paramétricas do plano para plotá-lo usando o SymPy. Para tanto, podemos usar os seguintes comandos:
from sympy import *
from sympy.plotting import plot3d_parametric_surface
var(’r,s’,real=True)
plot3d_parametric_surface(1+2*r,-1-r+s,1+s,
(r,-2,2),(s,-2,2),show=True,
xlabel=’$x$’,ylabel=’$y$’)
1.3.3 Equação geral do plano
Seja o plano determinado pelo ponto de ancoragem e pelos vetores diretores e . Sabemos que se, e somente se, , e são linearmente dependentes. Ou, equivalentemente, o produto misto . Logo,
| (1.114) | ||||
| (1.115) | ||||
| (1.116) | ||||
| (1.117) | ||||
| (1.118) |
Observamos que a equação acima tem a forma geral
| (1.119) |
com não todos nulos ou, equivalentemente, . Esta última é chamada equação geral do plano.
Exemplo 1.3.3.
No Exemplo 1.3.1, discutimos sobre o plano determinado pelo ponto e os vetores e . Para encontrarmos a equação geral deste plano, tomamos e calculamos
| (1.120) | ||||
| (1.121) | ||||
| (1.122) |
Ou seja, a equação geral deste plano é
| (1.123) |
1.3.4 Exercícios resolvidos
ER 1.3.1.
Seja um plano tal que , e . Determine uma equação vetorial para .
Solução 0.
Para obtermos uma equação vetorial do plano , precisamos de um ponto e dois vetores l.i. em . Do enunciado, temos o ponto e o vetor . Portanto, precisamos encontrar um vetor tal que e sejam l.i.. Por sorte, temos e, portanto . Podemos tomar
| (1.124) | ||||
| (1.125) |
pois e são l.i.. Logo, uma equação vetorial do plano é
| (1.126) | ||||
| (1.127) |
com .
ER 1.3.2.
Seja o plano de equações paramétricas
| (1.128) | |||
| (1.129) | |||
| (1.130) |
Determine o valor de de forma que .
Solução 0.
Para que pertença ao plano, devemos ter
| (1.131) | |||
| (1.132) | |||
| (1.133) |
Das duas primeiras equações, obtemos e . Daí, da terceira equação, temos
| (1.134) |
Exercícios
E. 1.3.1.
Determine a equação vetorial do plano com ponto de ancoragem e vetores diretores e .
Resposta 0.
E. 1.3.2.
Seja o plano de equação vetorial , , com ponto de ancoragem . Determine tal que pertença a este plano.
Resposta 0.
E. 1.3.3.
Determine as equações paramétricas do plano com ponto de ancoragem e vetores diretores e .
Resposta 0.
, ,
E. 1.3.4.
Considere o plano de equações paramétricas
| (1.135) | ||||
| (1.136) | ||||
| (1.137) |
Determine tal que pertença a este plano.
Resposta 0.
E. 1.3.5.
Determine a equação geral do plano com ponto de ancoragem e vetores diretores e .
Resposta 0.
E. 1.3.6.
Considere o plano de equação geral . Determine tal que o ponto pertença a este plano.
Resposta 0.
E. 1.3.7.
Considere o plano de equações paramétricas
| (1.138) | ||||
| (1.139) | ||||
| (1.140) |
A reta de equação paramétricas
| (1.141) | ||||
| (1.142) | ||||
| (1.143) |
é paralela ao plano ? Justifique sua resposta.
Resposta 0.
sim
E. 1.3.8.
Considere o plano de equação geral
| (1.144) |
Determine uma equação paramétrica para a reta que é perpendicular ao plano e passa pelo ponto .
Resposta 0.
, ,
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.
Geometria Analítica
Ajude a manter o site livre, gratuito e sem propagandas. Colabore!
1.3 Equações do plano
Em revisão
Um plano fica unicamente determinado por um ponto e dois vetores linearmente independentes 22endnote: 2No sentido que e têm representantes no plano .. Veja a Figura 1.9.

Os chamados vetores diretores e determinam infinitos planos paralelos entre si. O chamado ponto de ancoragem fixa um destes planos.
1.3.1 Equação vetorial do plano
Consideremos um plano determinado pelo ponto de ancoragem e os vetores diretores e (veja a Figura 1.10). Então, um ponto se, e somente se, é coplanar a e , i.e. , e são linearmente dependentes. Ou seja, se, e somente se, pode ser escrito como combinação linear de e . Isto nos fornece a chamada equação vetorial do plano
| (1.94) |

Exemplo 1.3.1.
Consideremos o plano determinado pelo ponto e pelos vetores e (Veja a Figura 1.11. Desta forma, uma equação vetorial para este plano é
| (1.95) |
para .

Tomando, por exemplo, e , obtemos
| (1.96) | ||||
| (1.97) | ||||
| (1.98) |
Observando que as coordenadas do ponto são iguais as coordenadas do vetor , temos
| (1.99) | ||||
| (1.100) | ||||
| (1.101) |
Ou seja, .
1.3.2 Equações paramétricas do plano
Seja um plano com ponto de ancoragem e vetores diretores e . Então, todo o ponto neste plano satisfaz a equação vetorial
| (1.102) |
para dados parâmetros . Assim, temos
| (1.103) | ||||
| (1.104) |
Portanto, temos
| (1.105) | ||||
| (1.106) | ||||
| (1.107) |
Ou, equivalentemente,
| (1.108) | ||||
| (1.109) | ||||
| (1.110) |
as quais são chamadas de equações paramétricas do plano.
Exemplo 1.3.2.
No Exemplo 1.3.1, discutimos sobre o plano determinado pelo ponto e os vetores e . Do que vimos acima, temos que
| (1.111) | ||||
| (1.112) | ||||
| (1.113) |
são equações paramétricas deste plano.
Podemos usar as equações paramétricas do plano para plotá-lo usando o SymPy. Para tanto, podemos usar os seguintes comandos:
from sympy import *
from sympy.plotting import plot3d_parametric_surface
var(’r,s’,real=True)
plot3d_parametric_surface(1+2*r,-1-r+s,1+s,
(r,-2,2),(s,-2,2),show=True,
xlabel=’$x$’,ylabel=’$y$’)
1.3.3 Equação geral do plano
Seja o plano determinado pelo ponto de ancoragem e pelos vetores diretores e . Sabemos que se, e somente se, , e são linearmente dependentes. Ou, equivalentemente, o produto misto . Logo,
| (1.114) | ||||
| (1.115) | ||||
| (1.116) | ||||
| (1.117) | ||||
| (1.118) |
Observamos que a equação acima tem a forma geral
| (1.119) |
com não todos nulos ou, equivalentemente, . Esta última é chamada equação geral do plano.
Exemplo 1.3.3.
No Exemplo 1.3.1, discutimos sobre o plano determinado pelo ponto e os vetores e . Para encontrarmos a equação geral deste plano, tomamos e calculamos
| (1.120) | ||||
| (1.121) | ||||
| (1.122) |
Ou seja, a equação geral deste plano é
| (1.123) |
1.3.4 Exercícios resolvidos
ER 1.3.1.
Seja um plano tal que , e . Determine uma equação vetorial para .
Solução 0.
Para obtermos uma equação vetorial do plano , precisamos de um ponto e dois vetores l.i. em . Do enunciado, temos o ponto e o vetor . Portanto, precisamos encontrar um vetor tal que e sejam l.i.. Por sorte, temos e, portanto . Podemos tomar
| (1.124) | ||||
| (1.125) |
pois e são l.i.. Logo, uma equação vetorial do plano é
| (1.126) | ||||
| (1.127) |
com .
ER 1.3.2.
Seja o plano de equações paramétricas
| (1.128) | |||
| (1.129) | |||
| (1.130) |
Determine o valor de de forma que .
Solução 0.
Para que pertença ao plano, devemos ter
| (1.131) | |||
| (1.132) | |||
| (1.133) |
Das duas primeiras equações, obtemos e . Daí, da terceira equação, temos
| (1.134) |
Exercícios
E. 1.3.1.
Determine a equação vetorial do plano com ponto de ancoragem e vetores diretores e .
Resposta 0.
E. 1.3.2.
Seja o plano de equação vetorial , , com ponto de ancoragem . Determine tal que pertença a este plano.
Resposta 0.
E. 1.3.3.
Determine as equações paramétricas do plano com ponto de ancoragem e vetores diretores e .
Resposta 0.
, ,
E. 1.3.4.
Considere o plano de equações paramétricas
| (1.135) | ||||
| (1.136) | ||||
| (1.137) |
Determine tal que pertença a este plano.
Resposta 0.
E. 1.3.5.
Determine a equação geral do plano com ponto de ancoragem e vetores diretores e .
Resposta 0.
E. 1.3.6.
Considere o plano de equação geral . Determine tal que o ponto pertença a este plano.
Resposta 0.
E. 1.3.7.
Considere o plano de equações paramétricas
| (1.138) | ||||
| (1.139) | ||||
| (1.140) |
A reta de equação paramétricas
| (1.141) | ||||
| (1.142) | ||||
| (1.143) |
é paralela ao plano ? Justifique sua resposta.
Resposta 0.
sim
E. 1.3.8.
Considere o plano de equação geral
| (1.144) |
Determine uma equação paramétrica para a reta que é perpendicular ao plano e passa pelo ponto .
Resposta 0.
, ,
Envie seu comentário
Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.