Política de uso de dados

Ao navegar por este site, você concorda com a política de uso de dados.

| | | |

Geometria Analítica

1 Retas e Planos 1.1 Sistema de coordenadas no espaço 1.3 Equações do plano

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.2 Equações da reta

Em revisão

Nesta seção, vamos desenvolver equações para a representação de retas no espaço tridimensional.

Refer to caption — Figura 1.5: Ilustração de uma reta $r$ em um sistema de coordenadas ortonormal.

1.2.1 Equação vetorial de uma reta

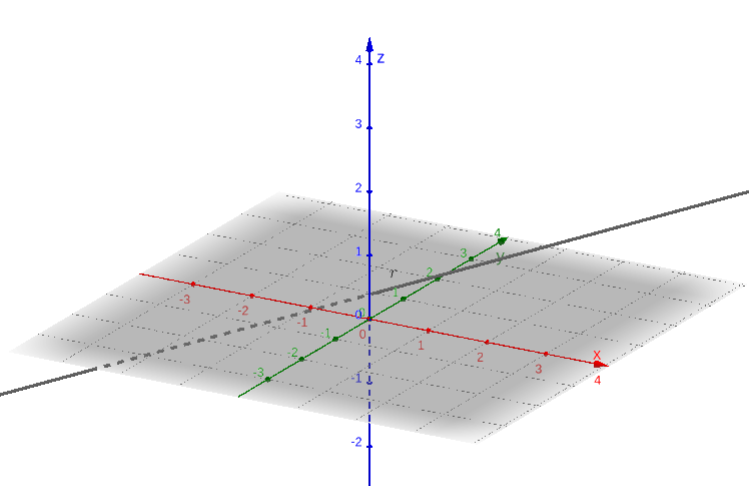
Seja $r$ uma reta dada, $\vec{v}$ um vetor paralelo a $r$ e $A$ um ponto de $r$ (veja a Figura 1.6). Assim sendo, $P=(x,y,z)$ é um ponto de $r$ se, e somente se, o vetor $\overrightarrow{AP}$ tem a mesma direção de $\vec{v}$ . i.e. existe $\lambda\in\mathbb{R}$ tal que

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}%\overrightarrow{AP}=\lambda\vec{v}}.

(1.32)

Esta é chamada equação vetorial da reta $r$ .

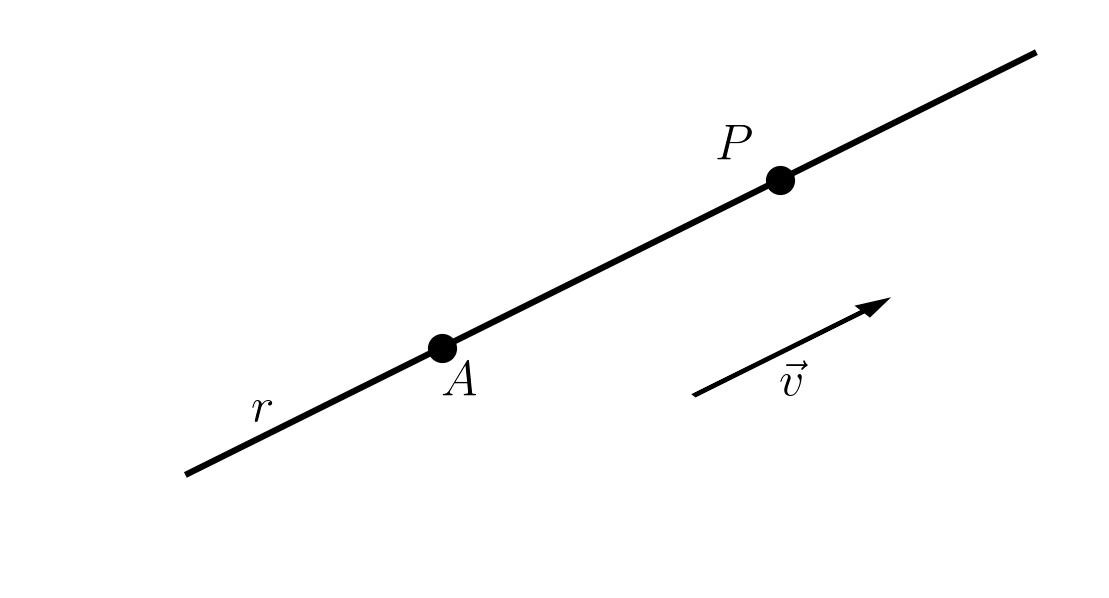
Observe que para obtermos uma equação vetorial de uma dada reta, podemos escolher qualquer ponto $A\in r$ e qualquer vetor $\vec{v}\parallel r$ , $\vec{v}\neq\vec{0}$ . O vetor $\vec{v}$ escolhido é chamado de vetor diretor.

Exemplo 1.2.1.

Seja $r$ a reta que passa pelos pontos $A=(-1,-1,-2)$ e $B=(2,1,3)$ (veja a Figura 1.7). O vetor

\vec{v}=\overrightarrow{AB}=(2-(-1),1-(-1),3-(-2))=(3,2,5)

(1.33)

é um vetor diretor de $r$ . Desta forma, uma equação vetorial da reta $r$ é

\overrightarrow{AP}=\lambda\vec{v}.

(1.34)

1.2.2 Equações paramétricas de uma reta

Seja $r$ uma reta que passa pelo ponto $A=(x_{A},y_{A},z_{A})$ e tenha vetor diretor $\vec{v}=(v_{1},v_{2},v_{3})$ . Da equação vetorial, temos que $P=(x,y,z)\in r$ se, e somente se, existe $\lambda\in\mathbb{R}$ tal que

\overrightarrow{AP}=\lambda\vec{v}.

(1.35)

Equivalentemente,

\underbrace{(x-x_{A},y-y_{A},z-z_{A})}_{\overrightarrow{AP}}=\lambda%\underbrace{(v_{1},v_{2},v_{3})}_{\vec{v}}.

(1.36)

Então,

$\displaystyle x-x_{A}$	$\displaystyle=\lambda v_{1},$	(1.37)
$\displaystyle y-y_{A}$	$\displaystyle=\lambda v_{2},$	(1.38)
$\displaystyle z-z_{A}$	$\displaystyle=\lambda v_{3},$	(1.39)

donde

$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}x}$	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}=x_{A}+\lambda v_{1}},$	(1.40)
$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}y}$	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}=y_{A}+\lambda v_{2}},$	(1.41)
$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}z}$	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}=z_{A}+\lambda v_{3}},$	(1.42)

as quais são chamadas de equações paramétricas da reta $r$ .

Exemplo 1.2.2.

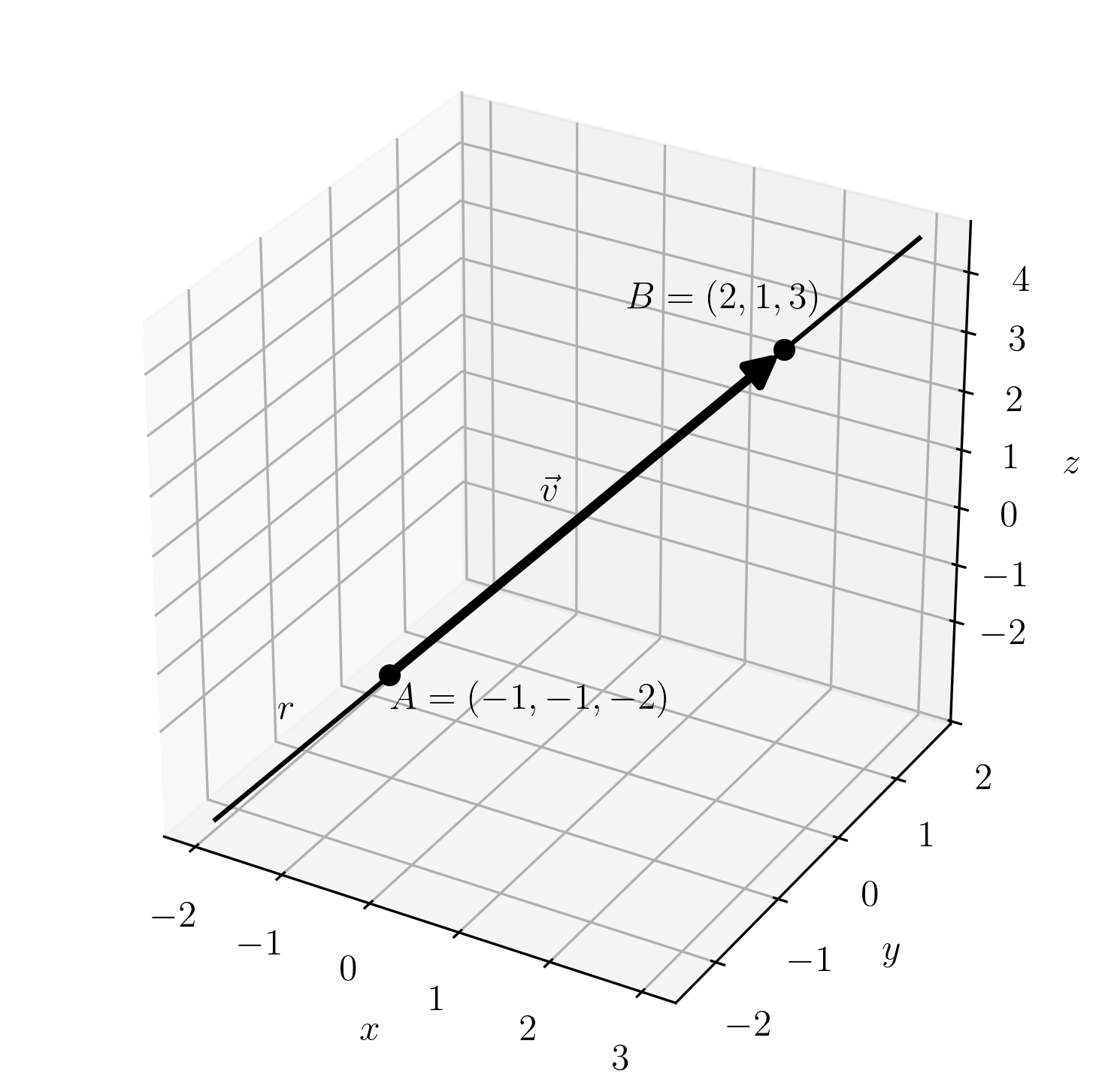
A reta $r$ discutida no Exemplo 1.2.1 tem equações paramétricas

$\displaystyle x$	$\displaystyle=-1+3\lambda,$	(1.43)
$\displaystyle y$	$\displaystyle=-1+2\lambda,$	(1.44)
$\displaystyle z$	$\displaystyle=-2+5\lambda.$	(1.45)

De fato, tomando $\lambda=0$ , temos $(x,y,z)=(-1,-1,-2)=A\in r$ . E, tomado $\lambda=1$ , temos $(x,y,z)=(-1+3,-1+2,-2+5)=(2,1,3)=B\in r$ . Ou seja, as equações paramétricas acima representam a reta que passa pelos pontos $A$ e $B$ .

Com o Sympy, podemos plotar o gráfico de $r$ usando o seguinte código:

var(’lbda’,real=True)
plot3d_parametric_line(-1+3*lbda,-1+2*lbda,-2+5*lbda,(lbda,-1,2))

1.2.3 Equações da reta na forma simétrica

Seja $r$ uma reta que passa pelo ponto $A=(x_{A},y_{A},z_{A})$ e tem $\vec{v}=(v_{1},v_{2},v_{3})$ como vetor diretor. Então, $r$ tem as equações paramétricas

$\displaystyle x$	$\displaystyle=x_{A}+v_{1}\lambda,$	(1.46)
$\displaystyle y$	$\displaystyle=y_{A}+v_{2}\lambda,$	(1.47)
$\displaystyle z$	$\displaystyle=z_{A}+v_{3}\lambda.$	(1.48)

Isolando $\lambda$ em cada uma das equações, obtemos

$\displaystyle\lambda$	$\displaystyle=\frac{x-x_{A}}{v_{1}},$	(1.49)
$\displaystyle\lambda$	$\displaystyle=\frac{y-y_{A}}{v_{2}},$	(1.50)
$\displaystyle\lambda$	$\displaystyle=\frac{z-z_{A}}{v_{3}}.$	(1.51)

Daí, temos

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\frac{x-x_{A%}}{v_{1}}=\frac{y-y_{A}}{v_{2}}=\frac{z-z_{A}}{v_{3}}},

(1.52)

as quais são as equações da reta na forma simétrica.

Exemplo 1.2.3.

No Exemplo 1.2.2, consideramos a reta $r$ de equações paramétricas

$\displaystyle x$	$\displaystyle=-1+3\lambda,$	(1.53)
$\displaystyle y$	$\displaystyle=-1+2\lambda,$	(1.54)
$\displaystyle z$	$\displaystyle=-2+5\lambda.$	(1.55)

Para obtermos as equações de $r$ na forma simétrica, basta isolarmos $\lambda$ em cada equação. Com isso, obtemos

\frac{x+1}{3}=\frac{y+1}{2}=\frac{z+2}{5}.

(1.56)

Exercícios resolvidos

ER 1.2.1.

Seja $r$ a reta que passa pelo ponto $A=(-1,-1,-2)$ e tem $\vec{v}=(3,2,5)$ como vetor diretor. Determine o valor de $x$ de forma que $P=\left(x,0,\frac{1}{2}\right)$ seja um ponto de $r$ .

Solução 0.

Da equação vetorial da reta $r$ , temos que $P=\left(x,0,\frac{1}{2}\right)$ é um ponto de $r$ se, e somente se, existe $\lambda\in\mathbb{R}$ tal que

\overrightarrow{AP}=\lambda\vec{v}.

(1.57)

Ou seja,

\left(x-(-1),0-(-1),\frac{1}{2}-(-2)\right)=\lambda(3,2,5).

(1.58)

Ou, equivalentemente,

\left(x+1,1,\frac{5}{2}\right)=\lambda(3,2,5).

(1.59)

Usando a segunda coordenada destes vetores, temos

	$\displaystyle 1=\lambda\cdot 2$		(1.60)
	$\displaystyle\lambda=\frac{1}{2}.$		(1.61)

Assim, da primeira coordenada dos vetores, temos

	$\displaystyle x+1=\lambda\cdot 3$		(1.62)
	$\displaystyle x+1=\frac{1}{2}\cdot 3$		(1.63)
	$\displaystyle x=\frac{3}{2}-1$		(1.64)
	$\displaystyle x=\frac{1}{2}.$		(1.65)

ER 1.2.2.

Seja $r$ a reta de equações paramétricas

$\displaystyle x$	$\displaystyle=1-\lambda,$	(1.66)
$\displaystyle y$	$\displaystyle=\lambda,$	(1.67)
$\displaystyle z$	$\displaystyle=-3.$	(1.68)

Determine uma equação vetorial de $r$ .

Solução 0.

Nas equações paramétricas de uma reta, temos que os coeficientes constantes estão associados a um ponto da reta. Os coeficientes do parâmetro $\lambda$ estão associados a um vetor diretor. Assim sendo, das equações paramétricas da reta $r$ , temos que

A=(1,0,-3)\in r

(1.69)

\vec{v}=(-1,1,0)

(1.70)

é um vetor diretor. Logo, temos que a reta $r$ tem equação vetorial

\overrightarrow{AP}=\lambda\vec{v},

(1.71)

com $A=(1,0,3)$ e $\vec{v}=(-1,1,0)$ .

ER 1.2.3.

Sabendo que $r$ é uma reta que passa pelos pontos $A=(2,-3,1)$ e $B=(-1,1,0)$ , determine o valor de $t$ tal que

$\displaystyle x$	$\displaystyle=2+t\lambda,$	(1.72)
$\displaystyle y$	$\displaystyle=-2+4\lambda,$	(1.73)
$\displaystyle z$	$\displaystyle=1-\lambda,$	(1.74)

sejam equações paramétricas de $r$ .

Solução 0.

Para que estas sejam equações paramétricas de $r$ , é necessário que $\vec{v}=(t,4,-1)$ seja um vetor diretor de $r$ . Em particular, $\vec{v}\parallel\overrightarrow{AB}$ . Logo, existe $\beta\in\mathbb{R}$ tal que

	$\displaystyle\vec{v}=\beta\overrightarrow{AB}$		(1.75)
	$\displaystyle(t,4,-1)=\beta(-1-2,1-(-3),0-1)$		(1.76)
	$\displaystyle(t,4,-1)=\beta(-3,4,-1).$		(1.77)

Das segunda e terceira coordenadas, temos $\beta=1$ . Daí, comparando pela primeira coordenada, temos

	$\displaystyle t=-3\beta$		(1.78)
	$\displaystyle t=-3.$		(1.79)

ER 1.2.4.

Seja $r$ uma reta de equações na forma simétrica

\frac{x+1}{2}=\frac{y-2}{3}=\frac{1-z}{2}.

(1.80)

Determine equações paramétricas para esta reta e faça um esboço de seu gráfico.

Solução 0.

Podemos obter equações paramétricas desta reta a partir de suas equações na forma simétrica. Para tanto, basta tomar o parâmetro $\lambda$ tal que

$\displaystyle\lambda$	$\displaystyle=\frac{x+1}{2},$	(1.81)
$\displaystyle\lambda$	$\displaystyle=\frac{y-2}{3},$	(1.82)
$\displaystyle\lambda$	$\displaystyle=\frac{1-z}{2}.$	(1.83)

Daí, isolando $x$ , $y$ e $z$ em cada uma destas equações, obtemos

$\displaystyle x$	$\displaystyle=-1+2\lambda,$	(1.84)
$\displaystyle y$	$\displaystyle=2+3\lambda,$	(1.85)
$\displaystyle z$	$\displaystyle=1-2\lambda.$	(1.86)

Para fazermos um esboço do gráfico desta reta, basta traçarmos a reta que passa por dois de seus pontos. Por exemplo, tomando $\lambda=0$ , temos $A=(-1,2,1)\in r$ . Agora, tomando $\lambda=1$ , temos $B=(1,5,-1)\in r$ . Desta forma, obtemos o esboço dado na Figura 1.8.

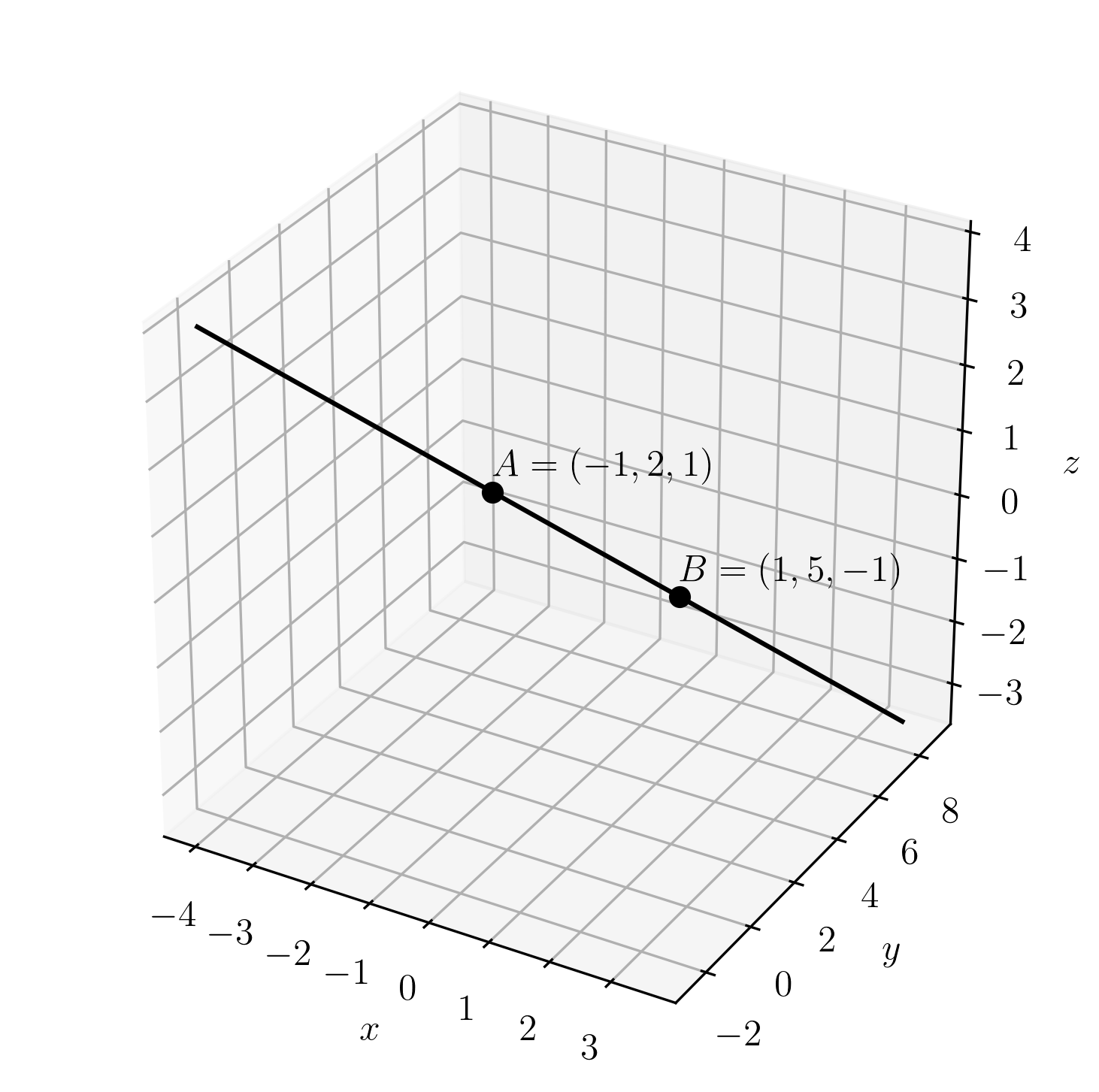
Exercícios

E. 1.2.1.

Seja a reta que passa pelos pontos $A=(1,-2,0)$ e $B=(-1,-1,1)$ . Determine:

a)

sua equação vetorial.
b)

suas equações paramétricas.
c)

suas equações na forma simétrica.

Resposta 0.

a) $\overrightarrow{AP}=\lambda\vec{v}$ , $\vec{v}=(-2,1,1)$ ; b) $x=1-2\lambda$ , $y=-2+\lambda$ , $z=\lambda$ ; c) $\frac{x-1}{-2}=y+2=z$

E. 1.2.2.

Seja a reta que passa pelo ponto $A=(0,1,-1)$ e tem vetor diretor $\vec{v}=(2,-1,1)$ . Determine $x$ tal que $B=(1,x,-\frac{1}{2})$ .

Resposta 0.

$x=\frac{1}{2}$

E. 1.2.3.

Considere a reta de equações na forma simétrica

\frac{x-1}{-2}=\frac{y+1}{3}=z-1.

(1.87)

Encontre um ponto e um vetor diretor desta reta.

Resposta 0.

$A=(1,-1,1)$ , $\vec{v}=(-2,3,1)$

E. 1.2.4.

Seja a reta $r$ de equações paramétricas

$\displaystyle x$	$\displaystyle=\lambda$	(1.88)
$\displaystyle y$	$\displaystyle=2-\lambda$	(1.89)
$\displaystyle z$	$\displaystyle=-1+\lambda$	(1.90)

Determine as equações na forma simétrica da reta que passa pelo ponto $A=(1,-1,0)$ e é paralela a reta $r$ .

Resposta 0.

$x-1=\frac{y+1}{-1}=z$

E. 1.2.5.

Seja a reta $r$ de equações paramétricas

$\displaystyle x$	$\displaystyle=\lambda$	(1.91)
$\displaystyle y$	$\displaystyle=2-\lambda$	(1.92)
$\displaystyle z$	$\displaystyle=-1+\lambda$	(1.93)

Determine as equações paramétricas da reta que passa pelo ponto $A=(1,-1,0)$ e é perpendicular a reta $r$ .

Resposta 0.

$x=1-\lambda$ , $y=-1-2\lambda$ , $z=-\lambda$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Geometria Analítica

1 Retas e Planos 1.1 Sistema de coordenadas no espaço 1.3 Equações do plano

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.2 Equações da reta

Em revisão

Nesta seção, vamos desenvolver equações para a representação de retas no espaço tridimensional.

1.2.1 Equação vetorial de uma reta

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}%\overrightarrow{AP}=\lambda\vec{v}}.

(1.32)

Esta é chamada equação vetorial da reta $r$ .

Exemplo 1.2.1.

Seja $r$ a reta que passa pelos pontos $A=(-1,-1,-2)$ e $B=(2,1,3)$ (veja a Figura 1.7). O vetor

\vec{v}=\overrightarrow{AB}=(2-(-1),1-(-1),3-(-2))=(3,2,5)

(1.33)

é um vetor diretor de $r$ . Desta forma, uma equação vetorial da reta $r$ é

\overrightarrow{AP}=\lambda\vec{v}.

(1.34)

1.2.2 Equações paramétricas de uma reta

\overrightarrow{AP}=\lambda\vec{v}.

(1.35)

Equivalentemente,

\underbrace{(x-x_{A},y-y_{A},z-z_{A})}_{\overrightarrow{AP}}=\lambda%\underbrace{(v_{1},v_{2},v_{3})}_{\vec{v}}.

(1.36)

Então,

$\displaystyle x-x_{A}$	$\displaystyle=\lambda v_{1},$	(1.37)
$\displaystyle y-y_{A}$	$\displaystyle=\lambda v_{2},$	(1.38)
$\displaystyle z-z_{A}$	$\displaystyle=\lambda v_{3},$	(1.39)

donde

$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}x}$	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}=x_{A}+\lambda v_{1}},$	(1.40)
$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}y}$	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}=y_{A}+\lambda v_{2}},$	(1.41)
$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}z}$	$\displaystyle{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1%}=z_{A}+\lambda v_{3}},$	(1.42)

as quais são chamadas de equações paramétricas da reta $r$ .

Exemplo 1.2.2.

A reta $r$ discutida no Exemplo 1.2.1 tem equações paramétricas

$\displaystyle x$	$\displaystyle=-1+3\lambda,$	(1.43)
$\displaystyle y$	$\displaystyle=-1+2\lambda,$	(1.44)
$\displaystyle z$	$\displaystyle=-2+5\lambda.$	(1.45)

Com o Sympy, podemos plotar o gráfico de $r$ usando o seguinte código:

var(’lbda’,real=True)
plot3d_parametric_line(-1+3*lbda,-1+2*lbda,-2+5*lbda,(lbda,-1,2))

1.2.3 Equações da reta na forma simétrica

Seja $r$ uma reta que passa pelo ponto $A=(x_{A},y_{A},z_{A})$ e tem $\vec{v}=(v_{1},v_{2},v_{3})$ como vetor diretor. Então, $r$ tem as equações paramétricas

$\displaystyle x$	$\displaystyle=x_{A}+v_{1}\lambda,$	(1.46)
$\displaystyle y$	$\displaystyle=y_{A}+v_{2}\lambda,$	(1.47)
$\displaystyle z$	$\displaystyle=z_{A}+v_{3}\lambda.$	(1.48)

Isolando $\lambda$ em cada uma das equações, obtemos

$\displaystyle\lambda$	$\displaystyle=\frac{x-x_{A}}{v_{1}},$	(1.49)
$\displaystyle\lambda$	$\displaystyle=\frac{y-y_{A}}{v_{2}},$	(1.50)
$\displaystyle\lambda$	$\displaystyle=\frac{z-z_{A}}{v_{3}}.$	(1.51)

Daí, temos

{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\frac{x-x_{A%}}{v_{1}}=\frac{y-y_{A}}{v_{2}}=\frac{z-z_{A}}{v_{3}}},

(1.52)

as quais são as equações da reta na forma simétrica.

Exemplo 1.2.3.

No Exemplo 1.2.2, consideramos a reta $r$ de equações paramétricas

$\displaystyle x$	$\displaystyle=-1+3\lambda,$	(1.53)
$\displaystyle y$	$\displaystyle=-1+2\lambda,$	(1.54)
$\displaystyle z$	$\displaystyle=-2+5\lambda.$	(1.55)

Para obtermos as equações de $r$ na forma simétrica, basta isolarmos $\lambda$ em cada equação. Com isso, obtemos

\frac{x+1}{3}=\frac{y+1}{2}=\frac{z+2}{5}.

(1.56)

Exercícios resolvidos

ER 1.2.1.

Seja $r$ a reta que passa pelo ponto $A=(-1,-1,-2)$ e tem $\vec{v}=(3,2,5)$ como vetor diretor. Determine o valor de $x$ de forma que $P=\left(x,0,\frac{1}{2}\right)$ seja um ponto de $r$ .

Solução 0.

Da equação vetorial da reta $r$ , temos que $P=\left(x,0,\frac{1}{2}\right)$ é um ponto de $r$ se, e somente se, existe $\lambda\in\mathbb{R}$ tal que

\overrightarrow{AP}=\lambda\vec{v}.

(1.57)

Ou seja,

\left(x-(-1),0-(-1),\frac{1}{2}-(-2)\right)=\lambda(3,2,5).

(1.58)

Ou, equivalentemente,

\left(x+1,1,\frac{5}{2}\right)=\lambda(3,2,5).

(1.59)

Usando a segunda coordenada destes vetores, temos

	$\displaystyle 1=\lambda\cdot 2$		(1.60)
	$\displaystyle\lambda=\frac{1}{2}.$		(1.61)

Assim, da primeira coordenada dos vetores, temos

	$\displaystyle x+1=\lambda\cdot 3$		(1.62)
	$\displaystyle x+1=\frac{1}{2}\cdot 3$		(1.63)
	$\displaystyle x=\frac{3}{2}-1$		(1.64)
	$\displaystyle x=\frac{1}{2}.$		(1.65)

ER 1.2.2.

Seja $r$ a reta de equações paramétricas

$\displaystyle x$	$\displaystyle=1-\lambda,$	(1.66)
$\displaystyle y$	$\displaystyle=\lambda,$	(1.67)
$\displaystyle z$	$\displaystyle=-3.$	(1.68)

Determine uma equação vetorial de $r$ .

Solução 0.

A=(1,0,-3)\in r

(1.69)

\vec{v}=(-1,1,0)

(1.70)

é um vetor diretor. Logo, temos que a reta $r$ tem equação vetorial

\overrightarrow{AP}=\lambda\vec{v},

(1.71)

com $A=(1,0,3)$ e $\vec{v}=(-1,1,0)$ .

ER 1.2.3.

Sabendo que $r$ é uma reta que passa pelos pontos $A=(2,-3,1)$ e $B=(-1,1,0)$ , determine o valor de $t$ tal que

$\displaystyle x$	$\displaystyle=2+t\lambda,$	(1.72)
$\displaystyle y$	$\displaystyle=-2+4\lambda,$	(1.73)
$\displaystyle z$	$\displaystyle=1-\lambda,$	(1.74)

sejam equações paramétricas de $r$ .

Solução 0.

	$\displaystyle\vec{v}=\beta\overrightarrow{AB}$		(1.75)
	$\displaystyle(t,4,-1)=\beta(-1-2,1-(-3),0-1)$		(1.76)
	$\displaystyle(t,4,-1)=\beta(-3,4,-1).$		(1.77)

Das segunda e terceira coordenadas, temos $\beta=1$ . Daí, comparando pela primeira coordenada, temos

	$\displaystyle t=-3\beta$		(1.78)
	$\displaystyle t=-3.$		(1.79)

ER 1.2.4.

Seja $r$ uma reta de equações na forma simétrica

\frac{x+1}{2}=\frac{y-2}{3}=\frac{1-z}{2}.

(1.80)

Determine equações paramétricas para esta reta e faça um esboço de seu gráfico.

Solução 0.

Podemos obter equações paramétricas desta reta a partir de suas equações na forma simétrica. Para tanto, basta tomar o parâmetro $\lambda$ tal que

$\displaystyle\lambda$	$\displaystyle=\frac{x+1}{2},$	(1.81)
$\displaystyle\lambda$	$\displaystyle=\frac{y-2}{3},$	(1.82)
$\displaystyle\lambda$	$\displaystyle=\frac{1-z}{2}.$	(1.83)

Daí, isolando $x$ , $y$ e $z$ em cada uma destas equações, obtemos

$\displaystyle x$	$\displaystyle=-1+2\lambda,$	(1.84)
$\displaystyle y$	$\displaystyle=2+3\lambda,$	(1.85)
$\displaystyle z$	$\displaystyle=1-2\lambda.$	(1.86)

Exercícios

E. 1.2.1.

Seja a reta que passa pelos pontos $A=(1,-2,0)$ e $B=(-1,-1,1)$ . Determine:

a)

sua equação vetorial.
b)

suas equações paramétricas.
c)

suas equações na forma simétrica.

Resposta 0.

a) $\overrightarrow{AP}=\lambda\vec{v}$ , $\vec{v}=(-2,1,1)$ ; b) $x=1-2\lambda$ , $y=-2+\lambda$ , $z=\lambda$ ; c) $\frac{x-1}{-2}=y+2=z$

E. 1.2.2.

Seja a reta que passa pelo ponto $A=(0,1,-1)$ e tem vetor diretor $\vec{v}=(2,-1,1)$ . Determine $x$ tal que $B=(1,x,-\frac{1}{2})$ .

Resposta 0.

$x=\frac{1}{2}$

E. 1.2.3.

Considere a reta de equações na forma simétrica

\frac{x-1}{-2}=\frac{y+1}{3}=z-1.

(1.87)

Encontre um ponto e um vetor diretor desta reta.

Resposta 0.

$A=(1,-1,1)$ , $\vec{v}=(-2,3,1)$

E. 1.2.4.

Seja a reta $r$ de equações paramétricas

$\displaystyle x$	$\displaystyle=\lambda$	(1.88)
$\displaystyle y$	$\displaystyle=2-\lambda$	(1.89)
$\displaystyle z$	$\displaystyle=-1+\lambda$	(1.90)

Determine as equações na forma simétrica da reta que passa pelo ponto $A=(1,-1,0)$ e é paralela a reta $r$ .

Resposta 0.

$x-1=\frac{y+1}{-1}=z$

E. 1.2.5.

Seja a reta $r$ de equações paramétricas

$\displaystyle x$	$\displaystyle=\lambda$	(1.91)
$\displaystyle y$	$\displaystyle=2-\lambda$	(1.92)
$\displaystyle z$	$\displaystyle=-1+\lambda$	(1.93)

Determine as equações paramétricas da reta que passa pelo ponto $A=(1,-1,0)$ e é perpendicular a reta $r$ .

Resposta 0.

$x=1-\lambda$ , $y=-1-2\lambda$ , $z=-\lambda$

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Pedro H A Konzen

| | | |