Pré-Cálculo

1 Números reais 1.1 Conjuntos numéricos 1.3 Conjunto dos números reais

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.2 Conjunto dos números racionais

Nesta seção, vamos estudar alguns aspectos fundamentais sobre o conjunto dos números racionais.

1.2.1 Números naturais

Os números naturais são os números de contagem

\mathbb{N}=\{0,1,2,3,\ldots\},

(1.42)

onde as reticências denotam a sequência dos números (consulte a Figura 1.8 para uma representação geométrica).

Refer to caption — Figura 1.8: Números naturais.

O conjunto dos números naturais pode ser construído dos axiomas de Peano²²2Giuseppe Peano, 1858 - 1932, matemático italiano. Fonte: Wikipédia.:

a)

$0$ é o único número natural que não é sucessor de nenhum outro;
b)

todo número natural $m\neq 0$ tem um sucessor $m+1$ ;
c)

números que têm o mesmo sucessor são iguais;
d)

se um subconjunto $A$ de números naturais contém o $0$ e contém o sucessor de cada um de seus elementos, então $A=\mathbb{N}$ ³³3Axioma do Princípio da Indução..

Código 12: Python

⬇

1from sympy import S

2print('0 in N?', 0 in S.Naturals0)

3print('1 in N?', 1 in S.Naturals0)

4print('-1 in N?', -1 in S.Naturals0)

0 in N? True

1 in N? True

-1 in N? False

Operações de adição e multiplicação

Nos números naturais $m,n\in\mathbb{N}$ estão bem definidas as operações usuais de:

a)

adição

$m+n=m+\underbrace{1+1+\cdots+1}_{n\text{ vezes}}$ (1.43)
b)

multiplicação

$m\cdot n=\underbrace{m+m+\cdots+m}_{n\text{ vezes}}$ (1.44)

Exemplo 1.2.1.

Vejamos os seguintes casos:

a)

$2+1=3$

Código 13: Python

⬇

12 + 1

⬇

3
b)

$1+2=3$
c)

$10+5=15$
d)

$3\cdot 2=6$

Código 14: Python

⬇

13 * 2

⬇

6
e)

$2\cdot 3=6$

Propriedades das operações

Sendo $m,n,p\in\mathbb{N}$ , temos ainda as seguintes propriedades fundamentais:

•

$0$ é o elemento neutro da adição

$m+0=m.$ (1.45)

Código 15: Python

⬇

1from sympy import Symbol

2m = Symbol('m', natural0=True)

3print('m + 0 = m?', m + 0 == m)

⬇

m + 0 = m? True
•

comutatividade da adição

$m+n=n+m$ (1.46)

Código 16: Python

⬇

1from sympy import symbols

2m, n = symbols('m, n', natural0=True)

3print('m + n = n + m?', m + n == n + m)

⬇

m + n = n + m? True
•

associatividade da adição

$m+(n+p)=(m+n)+p$ (1.47)
•

$1$ é o elemento neutro da multiplicação

$m\cdot 1=m.$ (1.48)
•

comutatividade da multiplicação

$m\cdot n=n\cdot m$ (1.49)
•

associatividade da multiplicação

$m\cdot(n\cdot p)=(m\cdot n)\cdot p$ (1.50)
•

distributividade da multiplicação em relação à adição

$m\cdot(n+p)=m\cdot n+m\cdot p$ (1.51)

Exemplo 1.2.2.

Verificamos as propriedades acima para casos específicos.

a)

Elemento neutro da adição

$5+0=5$ (1.52)
b)

Comutatividade da adição

$2+3=3+2$ (1.53)
c)

Associatividade da adição

$\displaystyle 2+(3+4)=2+7=9$ (1.54)

$\displaystyle(2+3)+4=5+4=9$ (1.55)
d)

Elemento neutro da multiplicação

$3\cdot 1=3$ (1.56)
e)

Comutatividade da multiplicação

$5\cdot 2=2\cdot 5=10$ (1.57)
f)

Associatividade da multiplicação

$\displaystyle 2\cdot(3\cdot 4)=2\cdot 12=24$ (1.58)

$\displaystyle(2\cdot 3)\cdot 4=6\cdot 4=24$ (1.59)
g)

Distributividade da multiplicação em relação à adição

$\displaystyle 2\cdot(3+4)=2\cdot 7=14$ (1.60)

$\displaystyle 2\cdot 3+2\cdot 4=6+8=14$ (1.61)

1.2.2 Números inteiros

O conjuntos dos números inteiros é

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\mathbb{Z}=\{% \ldots,-3,-2,-1,0,1,2,3,\ldots\}.

(1.62)

Os números com sinal negativo “ $-$ ” são definidos como sendo opostos aos respectivos números naturais. Mais precisamente, o oposto de um número $m$ é denotado por $-m$ e é tal que

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}m+(-m)=0.

(1.63)

Os números inteiros podem ser representados geometricamente como pontos sobre uma reta (consultemos a Figura 1.9). No centro, coloca-se o zero, à direita colocam-se os números positivos em ordem e igualmente espaçados. À esquerda do zero, colocam-se os números negativos, opostos aos respectivos números positivos.

Código 17: Python

⬇

1from sympy import S

2print('5 in Z?', 5 in S.Integers)

3print('0 in Z?', 0 in S.Integers)

4print('-3 in Z?', -3 in S.Integers)

5print('2.5 in Z?', 2.5 in S.Integers)

5 in Z? True

0 in Z? True

-3 in Z? True

2.5 in Z? False

Exemplo 1.2.3.

Consideramos os seguintes casos:

a)

$-1$ é o oposto de $1$ .

$1+(-1)=0$ (1.64)
b)

$2$ é o oposto de $-2$ .

$-2+2=0$ (1.65)

Os números inteiros contém os números naturais (consultemos a Figura 1.10), i.e.

\mathbb{N}\subset\mathbb{Z}.

(1.66)

Ainda, as operações de adição e multiplicação podem ser imediatamente estendidas para os números inteiros, assim como suas propriedades de elemento neutro, comutatividade, associatividade e distributividade.

Código 18: Python

⬇

1from sympy import S

2print(S.Naturals.is_subset(S.Integers))

True

Operação de Subtração

Com a definição de oposto, podemos definir a operação de subtração de dois números inteiros da seguinte forma

	$\displaystyle m-n=m+(-n)$		(1.67)
	$\displaystyle\text{}\quad=-n+m,$		(1.68)

sendo a operação de adição definida usualmente.

Código 19: Python

⬇

1from sympy import symbols

2m, n = symbols('m n', integer=True)

3print('m-n = n-m?', m-n == -n+m)

m-n = n-m? True

Exemplo 1.2.4.

	$\displaystyle 2-3=2+(-3)$		(1.69)
	$\displaystyle\text{}\quad=-3+2=-1$		(1.70)

Código 20: Python

⬇

12 - 3

-1

Valor absoluto

Dado um número $p\in\mathbb{Z}$ , definimos o seu valor absoluto⁴⁴4Também, chamado de módulo. pelo número inteiro

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}|p|=\left\{% \begin{array}[]{ll}p&,p\geq 0,\\ -p&,p<0.\end{array}\right.

(1.71)

Exemplo 1.2.5.

Estudemos os seguintes casos:

a)

$|3|=3$
b)

$|-2|=-(-2)=2$
c)

$|0|=0$

Código 21: Python

⬇

1from sympy import Abs, Symbol

2print('|3| =', Abs(3))

3print('|-2| =', Abs(2))

4print('|0| =', Abs(0))

5m = Symbol('m', integer=True, nonnegative=True)

6print('m >= 0, |-m| = ', Abs(-m))

|3| = 3

|-2| = 2

|0| = 0

m >= 0, |-m| = m

Para qualquer $p\in\mathbb{Z}$ , temos as seguintes propriedades:

a)

$|p|\geq 0$
b)

$|p|=0\Leftrightarrow p=0$
c)

$|p|=|-p|$
d)

$|p|<q\Leftrightarrow-q<p<q$
e)

$|p|>q\Leftrightarrow-p<-q\text{ ou }p>q$

1.2.3 Números racionais

O conjunto dos números racionais é

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\mathbb{Q}=% \left\{\frac{p}{q}:\leavevmode\nobreak\ p\in\mathbb{Z}\text{ e }q\in\mathbb{Z}% ^{*}\right\},

(1.72)

sendo $\mathbb{Z}^{*}=\mathbb{Z}\setminus\{0\}$ . O quociente $p/q$ é definido como sendo o resultado da operação de divisão de $p$ por $q$ , i.e.

\frac{p}{q}=x\Leftrightarrow p=x\cdot q.

(1.73)

Consultemos a Figura 1.11 para uma representação geométrica dos números racionais.

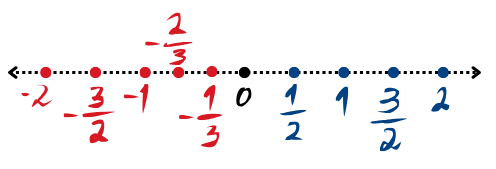
Observação 1.2.1.(Divisão por zero)

Não está definida a divisão por zero! Note que não existe $x$ tal que

\frac{p}{0}=x\Leftrightarrow p=0\cdot x.

(1.74)

Também, $0/0$ não está bem definido. Neste caso, temos uma indeterminação matemática⁵⁵5Indeterminação matemática é um conceito do cálculo de limites., de fato não existe um único número $x$ tal que

\frac{0}{0}=x\Leftrightarrow 0=0\cdot x.

(1.75)

A operação de adição de números racionais fica, então

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\frac{a}{b}+% \frac{c}{d}=\frac{a\cdot d+c\cdot b}{b\cdot d}

(1.76)

Observação 1.2.2.(Divisão e números racionais em Python)

Em Python, a operação de divisão é feita com o operador / e retorna um número decimal.

Código 22: Python

⬇

12/3

0.6666666666666666

Para obter o quociente de dois números inteiros, usamos a função S() do módulo sympy.

Código 23: Python

⬇

1from sympy import S

2S(2)/3

2/3

A definição de uma variável simbólica como número racional pode ser feita com o argumento rational=True da função Symbol() do módulo sympy.

Código 24: Python

⬇

1from sympy import Symbol

2x = Symbol('x', rational=True)

Exemplo 1.2.6.

	$\displaystyle\frac{2}{5}+\frac{3}{4}=\frac{2\cdot 4+3\cdot 5}{5\cdot 4}$		(1.77)
	$\displaystyle\text{}\quad=\frac{8+15}{20}$		(1.78)
	$\displaystyle\text{}\quad=\frac{23}{20}$		(1.79)

Código 25: Python

⬇

1from sympy import S

2S(2)/5 + S(3)/4

23/20

A operação de multiplicação fica, então

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}\frac{a}{b}% \cdot\frac{c}{d}=\frac{a\cdot c}{b\cdot d}.

(1.80)

Exemplo 1.2.7.

	$\displaystyle\frac{2}{5}\cdot\frac{3}{2}=\frac{\cancel{2}\cdot 3}{5\cdot% \cancel{2}}$		(1.81)
	$\displaystyle\text{}\quad=\frac{3}{5}$		(1.82)

Código 26: Python

⬇

1from sympy import S

2S(2)/5 * S(3)/2

3/5

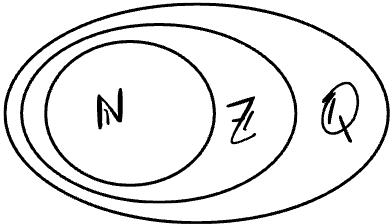
Observação 1.2.3.(Os números racionais, inteiros ou naturais)

\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}

(1.83)

Isso segue do fato de que se $m\in\mathbb{Z}$ , então

m=\frac{m}{1}.

(1.84)

Os números racionais também herdam as propriedades de elemento neutro, comutatividade, associatividade e distributividade nas operações de adição e multiplicação.

Operação de Potenciação

Outra operação fundamental é a operação de potenciação. A potenciação de um número racional $p/q\neq 0$ por um número natural $n$ é definida por

\left(\frac{p}{q}\right)^{n}=\underbrace{\frac{p}{q}\cdot\frac{p}{q}\cdot% \cdots\cdot\frac{p}{q}}_{n\text{ vezes}},

(1.85)

sendo $(p/q)^{0}=1$ . Ainda, definimos o inverso de um número racional $p/q$ por

\left(\frac{p}{q}\right)^{-1}=\frac{q}{p}.

(1.86)

Mais precisamente, o inverso de um número $x\neq 0$ é denotado por $x^{-1}$ e é tal que

x\cdot x^{-1}=1.

(1.87)

Com a escolha acima, vemos que $(p/q)^{-1}=q/p$ , pois

	$\displaystyle\frac{p}{q}\cdot\frac{q}{p}=\frac{p\cdot q}{q\cdot p}$		(1.88)
	$\displaystyle\text{}\quad=\frac{q\cdot p}{q\cdot p}$		(1.89)
	$\displaystyle\text{}\quad=\frac{q}{q}\cdot\frac{p}{p}$		(1.90)
	$\displaystyle\text{}\quad=1\cdot 1=1.$		(1.91)

Exemplo 1.2.8.

Verifiquemos os seguintes casos:

a)

$\displaystyle\left(\frac{3}{2}\right)^{3}=\frac{3}{2}\cdot\frac{3}{2}\cdot% \frac{3}{2}$ (1.92)

$\displaystyle\text{}\quad=\frac{9}{4}\cdot\frac{3}{2}$ (1.93)

$\displaystyle\text{}\quad=\frac{27}{8}$ (1.94)

Código 27: Python

⬇

1from sympy import S

2(S(3)/2)**3

⬇

27/8
b)

$\displaystyle 2^{3}=2\cdot 2\cdot 2$ (1.95)

$\displaystyle\text{}\quad=4\cdot 2$ (1.96)

$\displaystyle\text{}\quad=8$ (1.97)

Código 28: Python

⬇

12**3

⬇

8
c)

$\left(\frac{3}{2}\right)^{-1}=\frac{2}{3}$ (1.98)

Código 29: Python

⬇

1from sympy import S

2(S(3)/2)**-1

⬇

2/3

Sendo $a,b\in\mathbb{Q}$ e $n,m\in\mathbb{N}$ , temos as seguintes propriedades fundamentais da operação de potenciação⁶⁶6Estas propriedades são válidas desde que as operações estejam bem definidas. Por exemplo, a segunda propriedade elencada somente é válida no caso de $a\neq 0$ .:

•

$a^{m+n}=a^{m}\cdot a^{n}$
•

$\displaystyle a^{-m}=\left(a^{m}\right)^{-1}=\left(a^{-1}\right)^{m}$
•

$\displaystyle a^{m\cdot n}=\left(a^{m}\right)^{n}=\left(a^{n}\right)^{m}$
•

$\displaystyle\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}$

Observação 1.2.4.(Potências de zero não bem definidas)

As seguintes potenciações não estão bem definidas:

•

$0^{-1}$ não existe.

$0^{-1}=\frac{1}{0}\nexists$ (1.99)

O símbolo $\exists$ lê-se existe e o $\nexists$ lê-se não existe.
•

$0^{0}$ não está bem definida.

$\displaystyle 0^{0}=0^{1-1}$ (1.100)

$\displaystyle\text{}\quad=0^{1}\cdot 0^{-1}$ (1.101)

$\displaystyle\text{}\quad=0\cdot\cancelto{\nexists}{\frac{1}{0}}$ (1.102)

Enquanto que para $x\neq 0$ temos $x^{0}=1$ , $0^{0}$ não está bem definida! Trata-se de uma indeterminação, conceito introduzido em um curso de Cálculo.

Observação 1.2.5.( $0^{0}$ em Python)

Por convenção, no Python, $0^{0}=1$ .

Código 30: Python

⬇

10**0

Observação 1.2.6.(Razão irredutível)

A representatividade de números racionais não é única. Por exemplo,

\frac{2}{3}=\frac{4}{6}=\frac{14}{21}=\cdots

(1.103)

Isto nos motiva a introduzir o conceito de razão irredutível. Dizemos que $p/q$ é uma razão irredutível, quando $p$ e $q$ não têm divisor comum⁷⁷7Um número $m\in\mathbb{N}^{*}$ é divisor de $n\in\mathbb{Z}$ , quando $m/n\in\mathbb{Z}$ .. Por exemplo, $2/3$ é uma razão irredutível, enquanto $4/6$ não é, pois $4$ e $6$ têm $2$ como divisor comum.

1.2.4 Exercícios

E. 1.2.1.

Sejam $m,n,p,q\in\mathbb{N}$ . Argumente se são verdadeiras ou falsas as seguintes afirmações:

a)

$m=0+m$
b)

$m+(n+p)=(n+p)+m$
c)

$m+n+p=(n+m)+p$
d)

$(m+n)+(q+p)=(m+p)+(q+n)$
e)

$1\cdot m\neq m\cdot 1$
f)

$(m\cdot n)\cdot p=(n\cdot p)\cdot m$

a) V; b) V; c) V; d) V; e) F; f) V

E. 1.2.2.

Sejam $m,n,p,q\in\mathbb{Z}$ . Argumente se são verdadeiras ou falsas as seguintes afirmações:

a)

$n-p=p-n$
b)

$(m-n)+p=(m+p)-n$
c)

$-(-m)=m$

a) F; b) V; c) V

E. 1.2.3.

Mostre que

\frac{a}{b}+\frac{c}{d}=\frac{a\cdot d+b\cdot c}{b\cdot d},

(1.104)

onde $a,b,c,d\in\mathbb{Z}$ e $b,d\neq 0$ .

Dica: $a=bx$ e $c=dy$ , então $x+y=?$

E. 1.2.4.

O mínimo múltiplo comum dos números de dois números inteiros $c, d$ é denotado por $\operatorname{mmc}(c,d)$ e é o menor inteiro positivo que é múltiplo simultaneamente de $c$ e $d$ . Sendo, ainda, $a,b\in\mathbb{Z}$ e $c,d\neq 0$ , Mostre que

\frac{a}{c}+\frac{b}{d}=\frac{a\cdot\frac{\operatorname{mmc}(c,d)}{c}+b\cdot% \frac{\operatorname{mmc}(c,d)}{d}}{\operatorname{mmc}(c,d)}.

(1.105)

Qual a vantagem em usar o $\operatorname{mmc}$ para calcular a soma de frações?

No SymPy, o método sympy.ilcm computa o mínimo múltiplo comum de dois inteiros. Verifique!

Dica: $\displaystyle\frac{a}{c}+\frac{b}{d}=\frac{a\cdot d+b\cdot c}{c\cdot d}$

E. 1.2.5.

Mostre que

\frac{a}{b}\cdot\frac{c}{d}=\frac{a\cdot c}{b\cdot d},

(1.106)

onde $a,b,c,d\in\mathbb{Z}$ e $b,d\neq 0$ .

Dica: $a=bx$ e $c=dy$ , então $x\cdot y=?$

E. 1.2.6.

Sejam $p,q\in\mathbb{Q}$ , $q\neq 0$ , $m,n\in\mathbb{Z}$ . Argumente sobre a veracidade das seguintes afirmações.

a)

$q^{m-n}=\frac{q^{m}}{q^{n}}$
b)

$\displaystyle\left(\frac{p}{q}\right)^{m}=\frac{p^{m}}{q}$
c)

$q^{-m\cdot n}=\frac{q^{n}}{q^{m}}$

a) V; b) F; c) F

E. 1.2.7.

Verifique as seguintes desigualdades:

a)

$\displaystyle-\frac{3}{2}<\frac{1}{2}$
b)

$\displaystyle\frac{-2}{3}>-\frac{3}{4}$
c)

$\displaystyle\frac{4}{5}\geq\frac{5}{4}$
d)

$\displaystyle\frac{7}{2}\geq\frac{2}{3}$
e)

$\displaystyle-\frac{1}{2}<\frac{2}{-3}$

a) V; b) V; c) F; d) V; e) F

E. 1.2.8.

Sejam $a, b$ números racionais. Mostre que são verdadeiras os seguintes produtos notáveis:

a)

$(a+b)^{2}=a^{2}+2ab+b^{2}$
b)

$(a-b)^{2}=a^{2}-2ab+b^{2}$
c)

$(a+b)(a-b)=a^{2}-b^{2}$

a) $(a+b)^{2}=(a+b)\cdot(a+b)=(a+b)\cdot a+(a+b)\cdot b=a\cdot(a+b)+b\cdot(a+b)=a% \cdot a+a\cdot b+b\cdot a+b\cdot b=a^{2}+2ab+b^{2}$ . a) e b) seguem de maneira análoga.

E. 1.2.9.

Argumente sobre a veracidade das seguintes afirmações, onde $a,b\in\mathbb{Q}$ . Nos casos em que forem falsas, corrija-as.

a)

$\displaystyle\frac{a^{2}+b^{2}}{ab}=a+b$
b)

$\displaystyle\frac{a^{2}-b^{2}}{a-b}=a+b$ , para $a\neq b$
c)

$\displaystyle\frac{a+b}{a^{2}-b^{2}}=\frac{2}{a-b}$ , para $a\neq b$
d)

$\displaystyle\frac{a+b}{a}=1+b$ , para $a\neq 0$
e)

$\displaystyle\frac{a-ab}{a}=1-b$ , para $a\neq 0$

a) F; $\displaystyle\frac{a^{2}+b^{2}}{ab}=\frac{a}{b}+\frac{b}{a}$ ; b) V; c) F; $\displaystyle\frac{a+b}{a^{2}-b^{2}}=\frac{1}{a-b}$ ; d) F; $\displaystyle\frac{a+b}{a}=1+\frac{b}{a}$ ; e) V

E. 1.2.10.

$1+1=1$ ? Encontre o erro nos seguintes cálculos:

	$\displaystyle a=b$		(1.107)
	$\displaystyle a^{2}=ab$		(1.108)
	$\displaystyle a^{b}-b^{2}=ab-b^{2}$		(1.109)
	$\displaystyle(a+b)(a-b)=b(a-b)$		(1.110)
	$\displaystyle a+b=b$		(1.111)

Escolhendo, por exemplo, $a=1$ e $b=1$ , esta última fornece $1+1=1$ !

E. 1.2.11.

Seja $p,q\in\mathbb{Q}$ . Mostre as seguintes propriedades:

a)

$|p|\geq 0$
b)

$|p|=|-p|$
c)

$|p|<q\Leftrightarrow-q<p<q$
d)

$|p|>q\Leftrightarrow-p<-q\leavevmode\nobreak\ \text{ou}\leavevmode\nobreak\ p>q$

Dica: por definição, para $p\geq 0$ tem-se $|p|=p$ e, para $p<0$ tem-se $|p|=-p$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Pré-Cálculo

1.2 Conjunto dos números racionais

1.2.1 Números naturais

Operações de adição e multiplicação

Exemplo 1.2.1.

Propriedades das operações

Exemplo 1.2.2.

1.2.2 Números inteiros

Exemplo 1.2.3.

Operação de Subtração

Exemplo 1.2.4.

Valor absoluto

Exemplo 1.2.5.

1.2.3 Números racionais

Observação 1.2.1.(Divisão por zero)

Observação 1.2.2.(Divisão e números racionais em Python)

Exemplo 1.2.6.

Exemplo 1.2.7.

Observação 1.2.3.(Os números racionais, inteiros ou naturais)

Operação de Potenciação

Exemplo 1.2.8.

Observação 1.2.4.(Potências de zero não bem definidas)

Observação 1.2.5.( $0^{0}$ em Python)

Observação 1.2.6.(Razão irredutível)

1.2.4 Exercícios

E. 1.2.1.

E. 1.2.2.

E. 1.2.3.

E. 1.2.4.

E. 1.2.5.

E. 1.2.6.

E. 1.2.7.

E. 1.2.8.

E. 1.2.9.

E. 1.2.10.

E. 1.2.11.

Envie seu comentário

	$\displaystyle 2+(3+4)=2+7=9$		(1.54)
	$\displaystyle(2+3)+4=5+4=9$		(1.55)

	$\displaystyle 2\cdot(3\cdot 4)=2\cdot 12=24$		(1.58)
	$\displaystyle(2\cdot 3)\cdot 4=6\cdot 4=24$		(1.59)

	$\displaystyle 2\cdot(3+4)=2\cdot 7=14$		(1.60)
	$\displaystyle 2\cdot 3+2\cdot 4=6+8=14$		(1.61)

	$\displaystyle\left(\frac{3}{2}\right)^{3}=\frac{3}{2}\cdot\frac{3}{2}\cdot% \frac{3}{2}$		(1.92)
	$\displaystyle\text{}\quad=\frac{9}{4}\cdot\frac{3}{2}$		(1.93)
	$\displaystyle\text{}\quad=\frac{27}{8}$		(1.94)

	$\displaystyle 2^{3}=2\cdot 2\cdot 2$		(1.95)
	$\displaystyle\text{}\quad=4\cdot 2$		(1.96)
	$\displaystyle\text{}\quad=8$		(1.97)

	$\displaystyle 0^{0}=0^{1-1}$		(1.100)
	$\displaystyle\text{}\quad=0^{1}\cdot 0^{-1}$		(1.101)
	$\displaystyle\text{}\quad=0\cdot\cancelto{\nexists}{\frac{1}{0}}$		(1.102)

Política de uso de dados

Política de uso de dados

Pré-Cálculo

1.2 Conjunto dos números racionais

1.2.1 Números naturais

Operações de adição e multiplicação

Exemplo 1.2.1.

Propriedades das operações

Exemplo 1.2.2.

1.2.2 Números inteiros

Exemplo 1.2.3.

Operação de Subtração

Exemplo 1.2.4.

Valor absoluto

Exemplo 1.2.5.

1.2.3 Números racionais

Observação 1.2.1.(Divisão por zero)

Observação 1.2.2.(Divisão e números racionais em Python)

Exemplo 1.2.6.

Exemplo 1.2.7.

Observação 1.2.3.(Os números racionais, inteiros ou naturais)

Operação de Potenciação

Exemplo 1.2.8.

Observação 1.2.4.(Potências de zero não bem definidas)

Observação 1.2.5.(00 em Python)

Observação 1.2.6.(Razão irredutível)

1.2.4 Exercícios

E. 1.2.1.

E. 1.2.2.

E. 1.2.3.

E. 1.2.4.

E. 1.2.5.

E. 1.2.6.

E. 1.2.7.

E. 1.2.8.

E. 1.2.9.

E. 1.2.10.

E. 1.2.11.

Envie seu comentário

Observação 1.2.5.( $0^{0}$ em Python)