Pré-cálculo

1 Números reais 1 Números reais 1.2 Conjunto dos números racionais

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

1.1 Conjuntos numéricos

1.1.1 Definição de conjunto

Um conjunto $A$ é uma coleção de elementos ou objetos. Quando $x$ é um elemento do conjunto $A$ , denotamos

x\in A,

(1.1)

lê-se x pertence ao conjunto A. Já, a notação

x\not\in A

(1.2)

é usada para denotar que $x$ não pertence ao $A$ . A Figura 1.1 é uma representação gráfica (um diagrama de Venn¹¹1John Venn, 1834 - 1923, matemático inglês. Fonte: Wikipédia: John Venn.) de um conjunto $A$ com um elemento $x\in A$ .

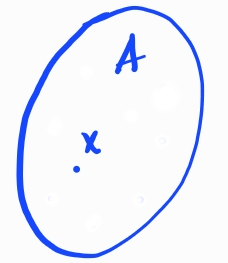
Refer to caption — Figura 1.1: Diagrama de Venn de um conjunto $A$ com elemento $x\in A$ .

Usualmente, um conjunto é descrito usando a notação

A=\{x:\leavevmode\nobreak\ \text{condi\c{c}\~{a}o para }x\},

(1.3)

lê-se $A$ é o conjunto dos elementos $x$ tais que $x$ satisfaz a condição.

Exemplo 1.1.1.

O conjunto $A$ formado por números positivos pode ser denotado por

A=\{x:x>0\}.

(1.4)

Ainda, observamos que $2\in A$ , $\sqrt{2}\in A$ , mas $-1\not\in A$ . Você saberia escolher mais elementos que pertencem ou que não pertencem a $A$ ?

Código 1: Python

⬇

1from sympy import Symbol, ConditionSet, sqrt

2x = Symbol('x')

3A = ConditionSet(x, x > 0)

4print('2 in A?', 2 in A)

5print('sqrt(2) in A?', sqrt(2) in A)

6print('-1 in A?', -1 in A)

2 in A? True

sqrt(2) in A? True

-1 in A? False

Conjunto finito

Conjunto finito é todo aquele que contém um número finito de elementos. Tais conjuntos podem ser descritos de forma simplificada como segue

A=\{a_{1},a_{2},\ldots,a_{n}\},

(1.5)

neste caso, temos um conjunto com $n$ elementos. Analogamente, um conjunto que contenha infinitos elementos é chamado de conjunto infinito.

Observação 1.1.1.

B=\{-1,3,2\}

(1.6)

é o conjunto que contém apenas os números $-1$ , $3$ e $2$ . Consultemos a representação geométrica de B na Figura 1.2.

Código 2: Python

⬇

1from sympy import FiniteSet

2A = FiniteSet(2, -1, 3)

3print('-1 in A?', -1 in A)

4print('sqrt(2) in A?', sqrt(2) in A)

-1 in A? True

sqrt(2) in A? False

Conjunto vazio

O conjunto que não contém elemento algum é chamado de conjunto vazio e é denotado por $\emptyset$ ou por $\{\}$ .

Código 3: Python

⬇

1from sympy import EmptySet

2print('-1 in {}?', -1 in EmptySet)

3print('0 in {}?', 0 in EmptySet)

4print('1 in {}?', 1 in EmptySet)

-1 in {}? False

0 in {}? False

1 in {}? False

Exemplo 1.1.2.

O conjunto $A$ de todos os números negativos e positivos é vazio, i.e.

A=\{x:x>0\text{ e }x<0\}=\emptyset

(1.7)

Igualdade de conjuntos

Dois conjuntos $A$ e $B$ são iguais, quando todos os elementos de $A$ pertencem a $B$ e vice-versa. Em notação matemática, escrevemos $A=B$ quando

x\in A\Leftrightarrow x\in B,

(1.8)

lê-se $x\in A$ se, e somente se, $x\in B$ .

Exemplo 1.1.3.

Estudemos os seguintes casos:

a)

São iguais os conjuntos

$\displaystyle A=\{-1,3,2\}$ (1.9)

$\displaystyle B=\{3,2,-1\},$ (1.10)

i.e. $A=B$ .

Código 4: Python

⬇

1from sympy import FiniteSet

2A = FiniteSet(-1, 3, 2)

3B = FiniteSet(3, 2, -1)

4A == B

⬇

True
b)

São diferentes os conjuntos

$\displaystyle C=\{-3,-2,-1,0\}$ (1.11)

$\displaystyle D=\{-3,-1,0,2\},$ (1.12)

i.e. $C\neq D$ . De fato, $-2\in C$ , mas $-2\not\in D$ . Também, $2\in D$ , mas $2\not\in C$ .

Código 5: Python

⬇

1from sympy import FiniteSet

2C = FiniteSet(-3, -2, -1, 0)

3D = FiniteSet(-3, -1, 0, 2)

4C != D

⬇

True

Subconjuntos

Dizemos que $A$ é subconjunto de $B$ , quando todos os elementos de $A$ pertencem a $B$ . Neste caso, denotamos

A\subset B

(1.13)

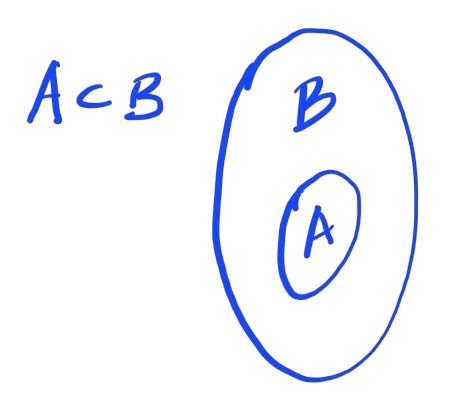
e lemos “A está contido em B”. Mais precisamente, $A\subset B$ quando

x\in A\Rightarrow x\in B,

(1.14)

lemos $x\in A$ implica $x\in B$ (consultemos a Figura 1.3). O mesmo pode ser denotado por $B\supset A$ , i.e. B contém A.

Exemplo 1.1.4.

Sejam os seguintes conjuntos

	$\displaystyle A=\{-1,3,2\}$		(1.15)
	$\displaystyle B=\{2,3\}.$		(1.16)

Temos que $B$ é subconjunto de $A$ , i.e. $B\subset A$ ( $B$ está contido em $A$ ). Entretanto, $A\not\subset B$ (A não está contido em B), pois $-1\in A$ , mas $-1\not\in B$ .

Código 6: Python

⬇

1from sympy import FiniteSet

2A = FiniteSet(-1, 3, 2)

3B = FiniteSet(2, 3)

4print('B <= A?', B.is_subset(A))

B <= A? True

Observação 1.1.2.(Conjunto vazio e subconjunto)

O conjunto vazio é subconjunto de qualquer conjunto $A$ , i.e.

\emptyset\subset A.

(1.17)

De fato, suponha que $\emptyset\not\subset A$ . Então, existe um elemento $x\in\emptyset$ tal que $x\not\in A$ . Um absurdo, pois o conjunto vazio não contém elemento algum.

1.1.2 Operações entre conjuntos

União de conjuntos

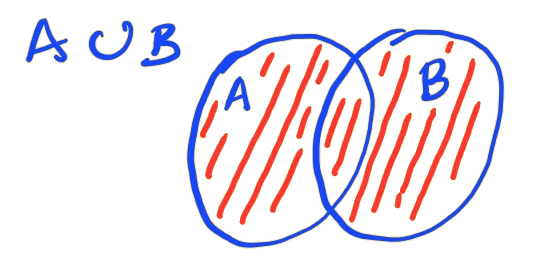
Sejam $A$ e $B$ dois conjuntos dados. A união do conjunto $A$ com o conjunto $B$ é o conjunto $A\cup B$ que contém todos os elementos que pertencem a $A$ ou a $B$ . Mais precisamente, temos

A\cup B=\{x:\leavevmode\nobreak\ x\in A\text{ ou }x\in B\},

(1.18)

lê-se o conjunto dos elementos $x$ tais que $x\in A$ ou $x\in B$ . Consultemos Figura 1.4.

Exemplo 1.1.5.

	$\displaystyle A=\{-1,3,2\}$		(1.19)
	$\displaystyle B=\{-2,0\},$		(1.20)

então

A\cup B=\{-2,-1,0,2,3\}.

(1.21)

Código 7: Python

⬇

1from sympy import FiniteSet

2A = FiniteSet(-1, 3, 2)

3B = FiniteSet(-2, 0)

4print('A | B =', A.union(B))

A | B = {-2, -1, 0, 2, 3}

Interseção de conjuntos

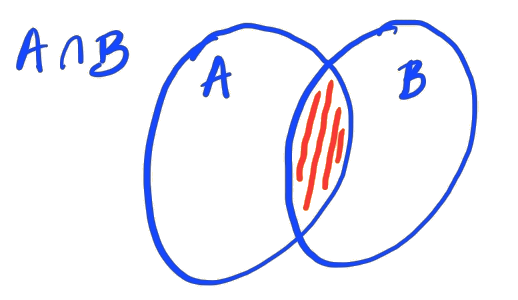
Sejam $A$ e $B$ dois conjuntos dados. A interseção do conjunto $A$ com o conjunto $B$ é o conjunto $A\cap B$ que contém os elementos que pertencem simultaneamente a ambos os conjuntos $A$ e $B$ . Mais precisamente, temos

A\cap B=\{x:\leavevmode\nobreak\ x\in A\text{ e }x\in B\},

(1.22)

lê-se o conjunto dos elementos $x$ tais que $x\in A$ e $x\in B$ . Consultemos a Figura 1.5.

Exemplo 1.1.6.

	$\displaystyle A=\{-1,3,2\}$		(1.23)
	$\displaystyle B=\{3,0\},$		(1.24)

então

A\cap B=\{3\}.

(1.25)

Código 8: Python

⬇

1from sympy import FiniteSet

2A = FiniteSet(-1, 3, 2)

3B = FiniteSet(3, 0)

4print('A & B =', A.intersection(B))

A & B = {3}

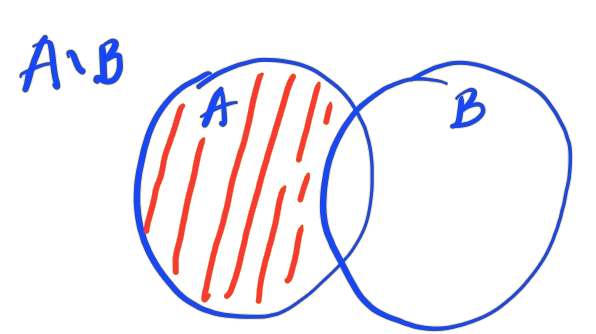
Diferença entre conjuntos

Sejam $A$ e $B$ dois conjuntos dados. A diferença (ou complemento relativo) do conjunto $A$ com o conjunto $B$ é o conjunto $A\setminus B$ que contém os elementos que pertencem ao $A$ e não pertencem ao conjunto $B$ . Mais precisamente, temos

A\setminus B=\{x:\leavevmode\nobreak\ x\in A\text{ e }x\not\in B\},

(1.26)

lê-se o conjunto dos elementos $x$ tais que $x\in A$ e $x\not\in B$ . Consultemos a Figura 1.6.

Exemplo 1.1.7.

	$\displaystyle C=\{-3,-2,-1,0\}$		(1.27)
	$\displaystyle D=\{-3,-1,0,2,4\},$		(1.28)

então

C\setminus D=\{-2\}.

(1.29)

Código 9: Python

⬇

1from sympy import FiniteSet

2A = FiniteSet(-3, -2, -1, 0)

3B = FiniteSet(-3, -1, 0, 2, 4)

4print('A - B =', A - B)

A - B = {-2}

Produto cartesiano

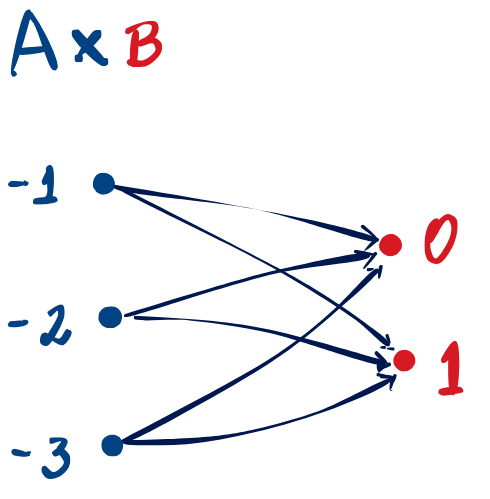
Sejam $A$ e $B$ dois conjuntos. O produto cartesiano de $A$ com $B$ é o conjunto $A\times B$ , cujos elementos são os pares ordenados $(x,y)$ com $x\in A$ e $y\in B$ . Mais precisamente, temos

A\times B=\{(x,y):\leavevmode\nobreak\ x\in A\text{ e }y\in B\},

(1.30)

lê-se o conjunto dos pares ordenados $(x,y)$ tais que $x\in A$ e $x\in B$ .

Observação 1.1.3.

Um par ordenado $(x,y)$ é um conjunto formado por $x$ e $y$ , no qual a posição dos elementos importa. Por exemplo, temos

(3,-1)\neq(-1,3),

(1.31)

enquanto que

\{3,-1\}=\{-1,3\}.

(1.32)

Código 10: Python

⬇

1A = (3, -1)

2B = (-1, 3)

3A == B

False

Exemplo 1.1.8.

	$\displaystyle A=\{-3,-2,-1\}$		(1.33)
	$\displaystyle B=\{0,1\},$		(1.34)

então

	$\displaystyle A\times B=\{(-3,0),(-2,0),(-1,0),$
	$\displaystyle\text{}\quad(-3,1),(-2,1),(-1,1)\}.$		(1.35)

Consultemos o esquemático do produto cartesiano na Figura 1.7.

Código 11: Python

⬇

1from sympy import FiniteSet, ProductSet

2A = FiniteSet(-3, -2, 1)

3B = FiniteSet(0, 1)

4C = ProductSet(A, B)

5print('C = ', set(C))

C = {(-3, 1), (-2, 1), (1, 1), (-3, 0), (-2, 0), (1, 0)}

1.1.3 Exercícios

E. 1.1.1.

Considere o seguinte conjunto

D=\{...,-3,-2,-1,0,1,2,3,...\}.

(1.36)

Em cada item, diga se é verdadeira ou falsa a afirmação. Justifique cada resposta.

a)

$-1\in D$
b)

$1\not\in D$
c)

$-5\not\in D$
d)

$\sqrt{100}\not\in D$
e)

$D$ é um conjunto finito

a) V; b) F; c) F; d) F; e) F

E. 1.1.2.

Dado $A=\{1,2,\{3,4\},5\}$ , determine se as seguintes afirmações são verdadeiras ou falsas. Justifique sua resposta.

a)

$\{2,5\}\subset A$
b)

$\{2,3\}\not\subset A$
c)

$\{3,4\}\subset A$
d)

$\{3,4\}\in A$
e)

$\{2,\{3,4\}\}\subset A$

a) V; b) V; c) F; d) V; e) V

E. 1.1.3.

Determine todos os subconjuntos de

\{1,-1,2,-3\}

(1.37)

$\emptyset$ , $\{1\}$ , $\{-1\}$ , $\{2\}$ , $\{-3\}$ , $\{1,-1\}$ , $\{1,2\}$ , $\{1,-3\}$ , $\{-1,2\}$ , $\{-1,-3\}$ , $\{2,-3\}$ , $\{1,-1,2\}$ , $\{1,-1,-3\}$ , $\{1,2,-3\}$ , $\{-1$ , $2$ , $-3\}$ , $\{1$ , $-1$ , $2$ , $-3\}$

E. 1.1.4.

Responda cada um dos seguintes itens:

a)

Quantos subconjuntos tem um conjunto de 5 elementos.
b)

Quantos elementos tem um conjunto que contém exatamente 16 subconjuntos.

a) $2^{5}=32$ ; b) $4$

E. 1.1.5.

Sejam os seguintes conjuntos

	$\displaystyle C=\{-4,2,-1,0,3\}$		(1.38)
	$\displaystyle D=\{5,-3,2,-4\}$		(1.39)

Determine os seguintes conjuntos:

a)

$C\cup D$
b)

$C\cap D$
c)

$C-D$
d)

$D-C$
e)

$C\cup\emptyset$
f)

$D\cap\emptyset$

a) $\{-4,-3,-1,0,2,3,5\}$ ; b) $\{-4,2\}$ ; c) $\{-1,0,3\}$ , d) $\{-3,5\}$ ; e) $C$ ; f) $\emptyset$

E. 1.1.6.

Seja $A$ um conjunto com 10 elementos e $B$ outro com 25. Sabendo que $A\cap B$ tem 5 elementos, determine o número de elementos do conjunto $A\cup B$ .

E. 1.1.7.

Sejam $A$ e $B$ conjuntos quaisquer. Diga se é verdadeira ou falsa cada uma das seguintes afirmações. Justifique sua resposta.

a)

$A\subset A\cup B$
b)

$A\cap B\supset A$
c)

$A\cup B\supset B$
d)

$A\cap B\subset A$
e)

$A\cup B\subset B$
f)

$(A\cup B)\cap A=\emptyset$

a) V; b) F; c) V; d) V; e) F; f) F

E. 1.1.8.

Sejam os seguintes conjuntos

	$\displaystyle C=\{-4,2\}$		(1.40)
	$\displaystyle D=\{5,-3,2,-4\}.$		(1.41)

Determine o conjunto $C\times D$ .

	$\displaystyle C\times D=\left\{(-4,5),(-4,-3),(-4,2),(-4,-4),\right.$		(1.42)
	$\displaystyle\text{}\quad\left.(2,5),(2,-3),(2,2),(2,-4)\right\}$		(1.43)

E. 1.1.9.

Justificando sua resposta, diga se é verdadeira a seguinte afirmação. Se $x\in A$ e $y\in B$ , então $(y,x)\in A\times B$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Pré-cálculo

1.1 Conjuntos numéricos

1.1.1 Definição de conjunto

Exemplo 1.1.1.

Conjunto finito

Observação 1.1.1.

Conjunto vazio

Exemplo 1.1.2.

Igualdade de conjuntos

Exemplo 1.1.3.

Subconjuntos

Exemplo 1.1.4.

Observação 1.1.2.(Conjunto vazio e subconjunto)

1.1.2 Operações entre conjuntos

União de conjuntos

Exemplo 1.1.5.

Interseção de conjuntos

Exemplo 1.1.6.

Diferença entre conjuntos

Exemplo 1.1.7.

Produto cartesiano

Observação 1.1.3.

Exemplo 1.1.8.

1.1.3 Exercícios

E. 1.1.1.

E. 1.1.2.

E. 1.1.3.

E. 1.1.4.

E. 1.1.5.

E. 1.1.6.

E. 1.1.7.

E. 1.1.8.

E. 1.1.9.

Envie seu comentário

	$\displaystyle A=\{-1,3,2\}$		(1.9)
	$\displaystyle B=\{3,2,-1\},$		(1.10)

	$\displaystyle C=\{-3,-2,-1,0\}$		(1.11)
	$\displaystyle D=\{-3,-1,0,2\},$		(1.12)