Pré-cálculo

3 Funções 3.3 Função potência 3.5 Função racional

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.4 Função polinomial

Uma função polinomial tem sua regra de associação dada por um polinômio, i.e. uma função da forma

p(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_{1}x+a_{0},

(3.78)

onde $a_{i}$ são coeficientes reais, $a_{n}\neq 0$ e $n$ é inteiro não negativo, este chamado de grau do polinômio.

Polinômios são definidos em toda parte⁴⁴4Uma função é dita ser definida em toda parte quando seu domínio é $(\infty,\infty)$ . Polinômios de grau ímpar têm imagem $(-\infty,\infty)$ . Entretanto, a imagem de polinômios de grau par dependem de cada caso. Iremos estudar mais propriedades de polinômios ao longo do curso de cálculo. Consultemos a Figura 3.20.

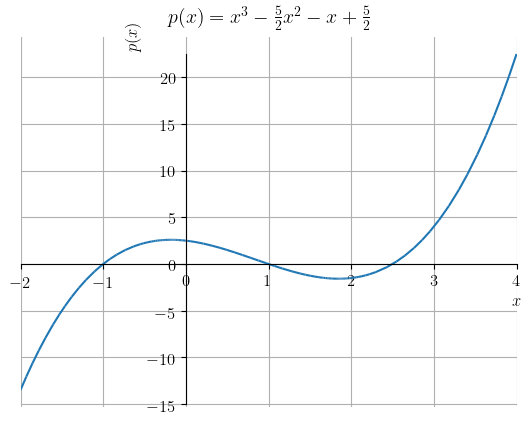
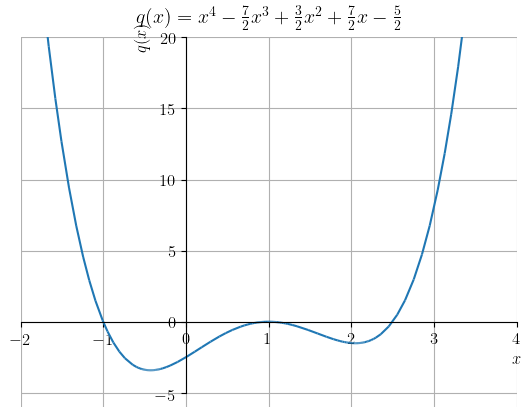
Refer to caption — Figura 3.20: Funções polinomiais: $p(x)=x^{3}-2.5x^{2}-1.0x+2.5$ (acima); $q(x)=x^{4}-3.5x^{3}+1.5x^{2}+3.5x-2.5$ (abaixo).

Quando $n=0$ , temos um polinômio de grau 0 (função constante). Quando $n=1$ , temos um polinômio de grau 1 (função afim ou linear). Ainda, quando $n=2$ temos uma função quadrática e, quando $n=3$ , temos uma função cúbica e assim por diante.

3.4.1 Função quadrática

Funções quadráticas são definidas por pol polinômios de grau 2, i.e. têm a forma

f(x)=ax^{2}+bx+c,

(3.79)

onde $a$ é chamado de coeficiente do termo quadrático, $b$ o coeficiente do termo linear e $c$ o coeficiente do termo constante.

Os zeros de uma função quadrática podem ser calculados pela fórmula de Bhaskara⁵⁵5Bhaskara Akaria, 1114 - 1185, matemático e astrônomo indiano. Fonte: Wikipédia: Bhaskara II.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}x_{0},x_{1}=% \frac{-b\pm\sqrt{b^{2}-4ac}}{2a}.

(3.80)

O esboço do gráfico de uma função quadrática é uma parábola côncava para cima quando $a>0$ e, côncava para baixo quando $x<0$ . Veja a Figura 3.21.

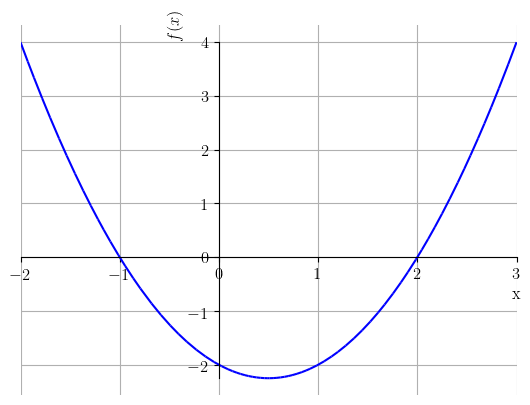
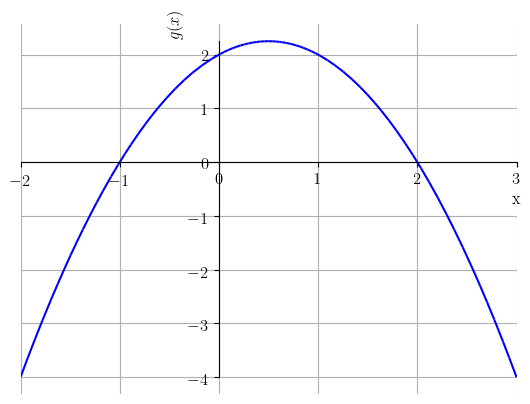
O vértice da parábola que representa uma função quadrática $f(x)$ com coeficiente quadrático positivo (com coeficiente quadrático negativo) é o ponto no qual ela atinge seu valor mínimo (máximo) em todo o seu domínio natural. Quando $f$ têm zeros reais, o ponto de abscissa do vértice é o ponto médio entre os zeros $x_{0}$ e $x_{1}$ da função, i.e. o vértice $V=(x_{v},y_{v})$ é tal que

x_{v}=\frac{x_{0}+x_{1}}{2},\quad\text{e}\quad y_{v}=f(x_{v}).

(3.81)

O valor $x_{v}$ é a abscissa do ponto em que a função quadrática $f$ atinge o valor máximo (valor mínimo) $y_{v}$ . Em geral, o vértice é dado por

(x_{v},y_{v})=\left(-\frac{b}{2a},-\frac{b^{2}-4ac}{4a}\right)

(3.82)

3.4.2 Técnica de completar o quadrado

A técnica de completar o quadrado, consiste em reescrever uma função quadrática

f(x)=ax^{2}+bx+c

(3.83)

na forma

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}f(x)=a(x-h)^{% 2}+k,

(3.84)

onde $h=-b/(2a)$ e $k$ é, portanto,

k=ax^{2}+bx+c-a(x-h)^{2}.

(3.85)

A forma (3.84) é útil para resolver equações quadráticas, traçar o gráfico de uma função quadrática, entre várias aplicações na disciplina de Cálculo.

Exemplo 3.4.1.

Vamos completar o quadrado da função quadrática

f(x)=2x^{2}-4x+1.

(3.86)

Temos que $a=2$ , $b=-4$ e $c=1$ e queremos reescrever $f$ na forma

f(x)=2(x-h)^{2}+k.

(3.87)

Para tanto, colocamos o coeficiente $a$ em evidência

f(x)=2\left(x^{2}{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{% 0,0,1}-2}x\right)+1

(3.88)

Lembrando do produto notável

(x-h)^{2}=x^{2}{\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{% 0,0,1}-2h}x+h^{2},

(3.89)

escolhemos $h=1$ . Logo,

	$\displaystyle f(x)=2\left((x-1)^{2}-1\right)+1$		(3.90)
	$\displaystyle\text{}\quad=2(x-1)^{2}-2+1$		(3.91)
	$\displaystyle\text{}\quad=2(x-1)^{2}-1.$		(3.92)

Observação 3.4.1.(Fórmula de Bhaskara)

A fórmula de Bhaskara (3.80) é uma aplicação direta da técnica de completar o quadrado. Para ver isso, basta reescrever a função quadrática $f(x)=ax^{2}+bx+c$ na forma (3.84) e igualar a zero. Consultemos o E.3.4.7.

3.4.3 Exercícios Resolvidos

ER 3.4.1.

Determine os zeros do polinômio $f(x)=x^{3}-x^{2}-2x$ .

Resolução.

Determinar os zeros da função $f$ significa encontrar todos os valores de $x$ tais que $f(x)=0$ (estes são as abscissas dos pontos nos quais o gráfico de $f$ intercepta o eixo das abscissas). Temos

	$\displaystyle f(x)=0$		(3.93)
	$\displaystyle x^{3}-x^{2}-2x=0$		(3.94)
	$\displaystyle x(x^{2}-x-2)=0$		(3.95)
	$\displaystyle x=0\quad\text{ou}\quad x^{2}-x-2=0.$		(3.96)

Então, usando a fórmula de Bhaskara (3.80) na equação $x^{2}-x-2=0$ , obtemos

	$\displaystyle x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$		(3.97)
	$\displaystyle\text{}\quad=\frac{1\pm\sqrt{1-4\cdot 1\cdot(-2)}}{2}$		(3.98)
	$\displaystyle\text{}\quad=\frac{1\pm\sqrt{9}}{2}$		(3.99)
	$\displaystyle\text{}\quad=\frac{1\pm 3}{2}$		(3.100)
	$\displaystyle\text{}\quad=-1\text{ ou }2$		(3.101)

Com isso, temos que os zeros da função $f$ ocorrem nos pontos $x_{0}=-1$ , $x_{1}=0$ e $x_{2}=2$ .

ER 3.4.2.

Determine o valor mínimo da função $f(x)=x^{2}-x-2$ .

Resolução.

Como $f$ é uma função quadrática com coeficiente quadrático positivo, temos que seu gráfico é uma parábola côncava para cima. Logo, $f$ atinge seu valor mínimo no seu vértice, que tem abscissa

	$\displaystyle x_{v}=-\frac{b}{2a}$		(3.102)
	$\displaystyle\text{}\quad=-\frac{-1}{2\cdot 1}$		(3.103)
	$\displaystyle\text{}\quad=\frac{1}{2}.$		(3.104)

Ou seja, a abscissa do ponto de mínimo de $f$ é $x_{v}=1/2$ e seu valor mínimo é

	$\displaystyle f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{2}-\frac{1}{% 2}-2$		(3.105)
	$\displaystyle\text{}\quad=\frac{1-2-8}{4}$		(3.106)
	$\displaystyle\text{}\quad=-\frac{9}{4}.$		(3.107)

3.4.4 Exercícios

E. 3.4.1.

Faça o esboço dos gráficos das seguintes funções polinomiais:

1.

$f(x)=1$
2.

$g(x)=-x+1$
3.

$h(x)=x^{2}-1$
4.

$f_{1}(x)=x^{3}$

E. 3.4.2.

Determine os zeros do polinômio $f(x)=-x^{3}+x^{2}+2x$ .

$-1$ , $0$ , $2$

E. 3.4.3.

Determine o valor máximo da função $f(x)=-x^{2}+x+2$ .

$9/4$

E. 3.4.4.

Faça um esboço da região determinada entre os gráficos de $y=0$ e $y=x^{2}-1$ , com $-1\leq x\leq 1$ .

E. 3.4.5.

Determine os pontos de interseção dos gráficos de $f(x)=-x+1$ e $f(x)=x^{2}-1$ .

$(-2,3)$ , $(1,0)$

E. 3.4.6.

(Aplicação.) Na mecânica clássica, a energia cinética $E_{c}$ de um objeto não rotativo de massa $m$ [kg] movimentando-se com uma velocidade $v$ [ $\text{m}/\text{s}$ ] é dada por

E_{c}=\frac{m}{2}v^{2}

(3.108)

Assumindo $m>0$ constante, temos que $E_{c}$ é função apenas de $v$ , i.e. $E_{c}=E_{c}(v)$ . Responda cada um dos seguintes itens:

a)

Qual a classe da função $E_{c}=E_{c}(v)$ ?
b)

Qual o domínio da função $E_{c}=E_{c}(v)$ .
c)

Qual a imagem da função $E_{c}=E_{c}(v)$ .
d)

A função $E_{c}=E_{c}(v)$ tem valor mínimo? Se sim, qual é esse valor e para o valor de $v$ em que isso ocorre?

a) função quadrática. b) $D(E_{v})=\{v\in\mathbb{R}:\leavevmode\nobreak\ -c\leq v\leq c\}$ , onde $c$ denota a velocidade da luz. c) $Im(E_{v})=\{e\in\mathbb{R}:0\leq e\leq\frac{m\cdot c^{2}}{2}\}$ , onde $c$ denota a velocidade da luz. d) Sim. Valor mínimo $E_{c}=0$ . Ponto de mínimo $v=0$ .

E. 3.4.7.

Use a técnica de completar o quadrado para mostrar que os zeros de uma função quadrática $f(x)=ax^{2}+bx+c$ são dados pela fórmula de Bhaskara (3.80).

Dica: mostre que

ax^{2}+bx+c=a\left(x+\frac{b}{2a}\right)^{2}-\frac{b^{2}-4ac}{4a}.

(3.109)

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados

Política de uso de dados

Pré-cálculo

3.4 Função polinomial

3.4.1 Função quadrática

3.4.2 Técnica de completar o quadrado

Exemplo 3.4.1.

Observação 3.4.1.(Fórmula de Bhaskara)

3.4.3 Exercícios Resolvidos

ER 3.4.1.

Resolução.

ER 3.4.2.

Resolução.

3.4.4 Exercícios

E. 3.4.1.

E. 3.4.2.

E. 3.4.3.

E. 3.4.4.

E. 3.4.5.

E. 3.4.6.

E. 3.4.7.

Envie seu comentário