Pré-cálculo

3 Funções 3.1 Definição e gráfico de funções 3.3 Função potência

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.2 Função afim

Uma função afim é uma função da forma

f(x)=mx+b,

(3.37)

sendo $m$ e $b$ parâmetros²²2números reais. dados. O parâmetro $m$ é chamado de coeficiente angular e o parâmetro $b$ é chamado de coeficiente constante³³3Em função afim $y=mx+b$ , $b$ é mais corretamente chamado de coeficiente do termo constante..

Quando $m=0$ , temos uma função constante $f(x)=b$ . Esta tem domínio $(-\infty,\infty)$ e imagem $\{b\}$ .

Quando $m\neq 0$ e $b=0$ , temos uma função linear $f(x)=mx$ , cujo domínio é $(-\infty,\infty)$ e imagem é $(-\infty,\infty)$ . De forma geral, toda função afim com $m\neq 0$ tem $(-\infty,\infty)$ como domínio e imagem.

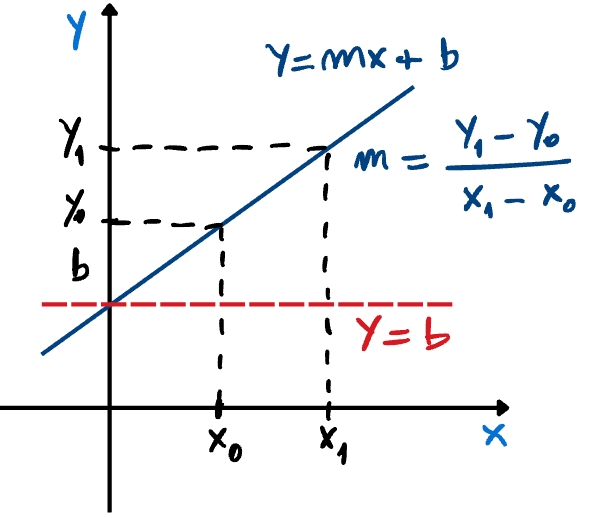
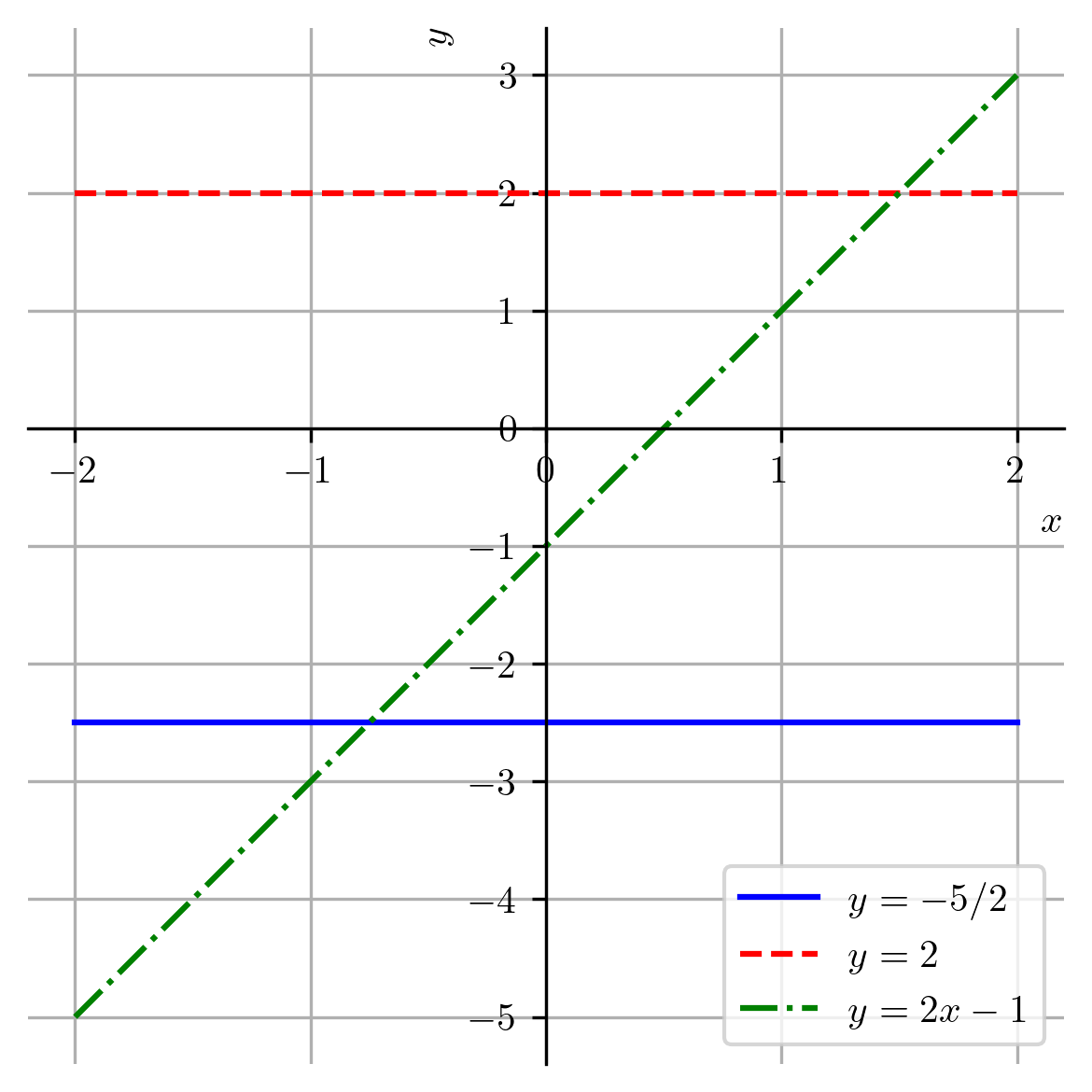
Refer to caption — Figura 3.6: Gráfico de funções afins $y=mx+b$ . Linha contínua: $m\neq 0$ . Linha tracejada: $m=0$ (função constante).

Exemplo 3.2.1.

A Figura 3.7 mostra esboços dos gráficos das funções afins $f(x)=-5/2$ , $g(x)=2$ e $h(x)=2x-1$ .

Código 40: Python

⬇

1from sympy import Symbol, plot

2x = Symbol('x')

3# gráficos de f(x)=-5/2, g(x)=2 e h(x)=2x-1

4plot(-5/2, 2, 2*x - 1, (x, -2, 2))

3.2.1 Retas e coeficiente angular

O lugar geométrico do gráfico de uma função afim é uma reta. O coeficiente angular $m$ controla a inclinação da reta em relação ao eixo $x$ . Quando $m=0$ , temos uma reta horizontal. Quando $m>0$ temos uma reta com inclinação positiva (crescente) e, quando $m<0$ temos uma reta com inclinação negativa.

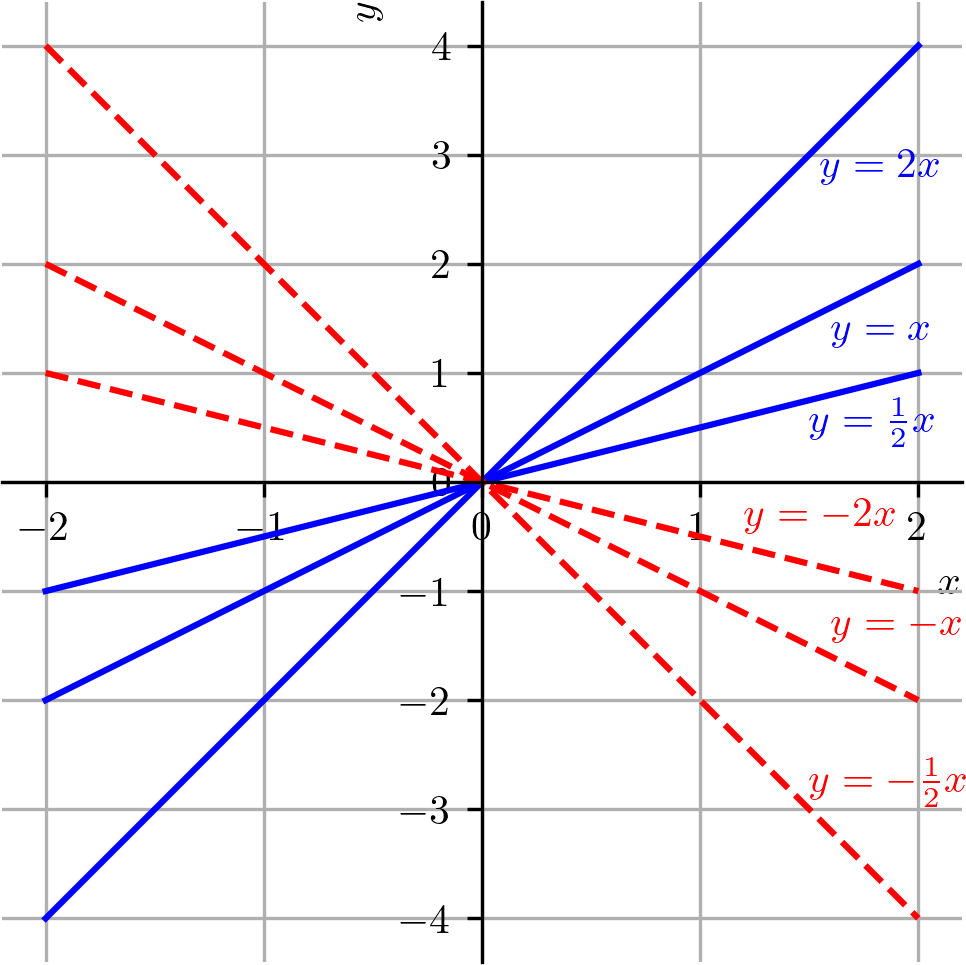
Exemplo 3.2.2.

A Figura 3.8 mostra esboços dos gráficos das funções lineares $f_{1}(x)=\frac{1}{2}x$ , $f_{2}(x)=x$ , $f_{3}(x)=2x$ , $f_{4}(x)=-2x$ , $f_{5}(x)=-x$ e $f_{6}(x)=-\frac{1}{2}x$ .

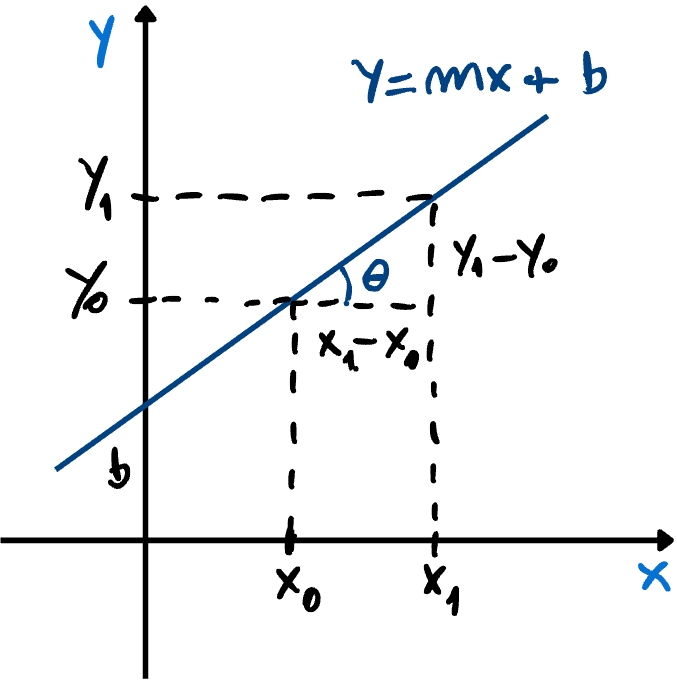
A inclinação de uma reta é, normalmente, medida pelo ângulo de declividade (veja a Figura 3.9). Para definirmos este ângulo, sejam $(x_{0},y_{0})$ e $(x_{1},y_{1})$ , $x_{0}<x_{1}$ , pontos sobre uma dada reta, gráfico da função afim $f(x)=mx+b$ . O ângulo de declividade (ou, simplesmente, a declividade) da reta é, por definição, o ângulo formado pelo segmento que parte de $(x_{0},y_{0})$ e termina em $(x_{1},y_{0})$ e o segmento que parte de $(x_{0},y_{0})$ e termina em $(x_{1},y_{1})$ . Denotando este ângulo por $\theta$ , temos

	$\displaystyle\operatorname{tg}\theta=\frac{\text{cateto oposto}}{\text{cateto % adjacente}}$		(3.38)
	$\displaystyle\text{}\quad=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}$		(3.39)
	$\displaystyle\text{}\quad=\frac{mx_{1}+b-(mx_{0}+b)}{x_{1}-x_{0}}$		(3.40)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \operatorname{tg}\theta=m.$		(3.41)

Ou seja, o coeficiente angular $m$ é a tangente do ângulo de declividade da reta.

Quaisquer dois pontos $(x_{0},y_{0})$ e $(x_{1},y_{1})$ , com $x_{0}\neq x_{1}$ , determinam uma única função afim (reta) que passa por estes pontos. Para encontrar a expressão desta função, basta resolver o seguinte sistema linear

	$\displaystyle mx_{0}+b=y_{0}$		(3.42)
	$\displaystyle mx_{1}+b=y_{1}$		(3.43)

Subtraindo a primeira equação da segunda, obtemos

	$\displaystyle m(x_{0}-x_{1})=y_{0}-y_{1}$		(3.44)
	$\displaystyle m=\frac{y_{0}-y_{1}}{x_{0}-x_{1}}$		(3.45)

Daí, substituindo o valor de $m$ na primeira equação do sistema, obtemos

	$\displaystyle\frac{y_{0}-y_{1}}{x_{0}-x_{1}}x_{0}+b=y_{0}$		(3.46)
	$\displaystyle b=-\frac{y_{0}-y_{1}}{x_{0}-x_{1}}x_{0}+y_{0}$		(3.47)

Ou seja, a expressão da função afim (equação da reta) que passa pelos pontos $(x_{0},y_{0})$ e $(x_{1},y_{1})$ é

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}y=\underbrace% {\frac{y_{0}-y_{1}}{x_{0}-x_{1}}}_{m}(x-x_{0})+y_{0}.

(3.48)

Exemplo 3.2.3.

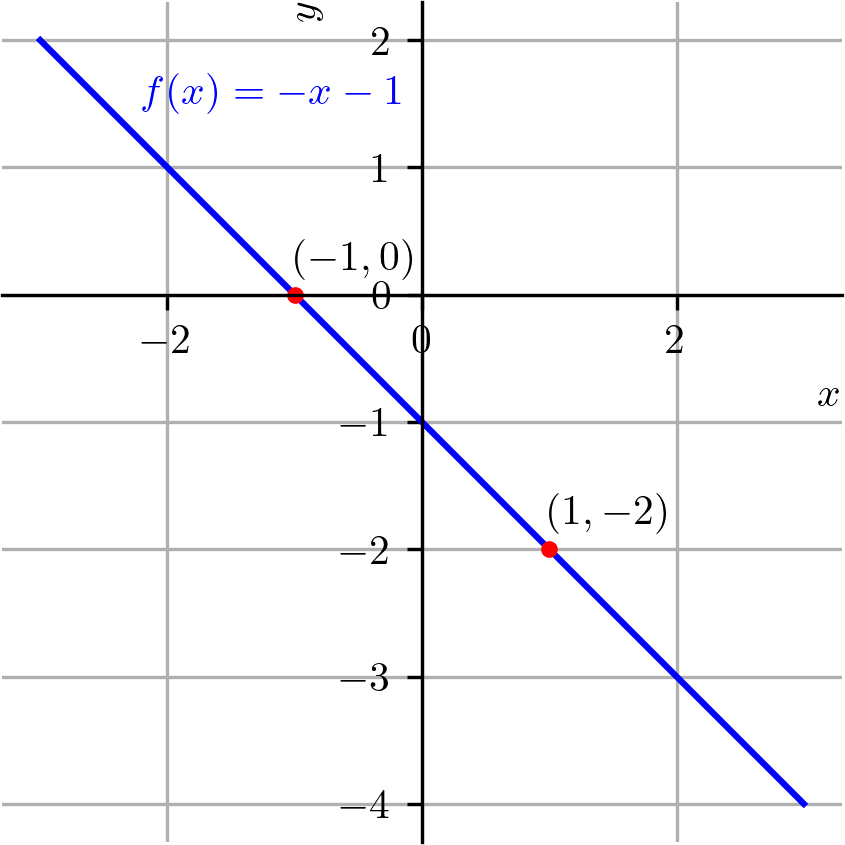
Vamos traçar a reta que representa o gráfico da função afim $f(x)=-x-1$ . Para tanto, basta traçarmos a reta que passa por quaisquer dois pontos distintos de seu gráfico. Por exemplo, no caso da função $f(x)=-x-1$ , temos

$x$	$y=-x-1$
-1	0
1	-2

Assim sendo, marcamos os pontos $(-1,0)$ e $(1,-2)$ em um plano cartesiano e traçamos a reta que passa por eles. Consulte a Figura 3.10.

Exemplo 3.2.4.

Vamos determinar a função afim $f(x)=mx+b$ , cujo gráfico contém os pontos $(1,-1)$ e $(2,1)$ . Para tanto, vamos usar (3.48). Tomamos

	$\displaystyle(x_{0},y_{0})=(1,-1)$		(3.49)
	$\displaystyle(x_{1},y_{1})=(2,1)$		(3.50)

Então, substituindo em (3.48) temos

m=\frac{y_{1}-y_{0}}{x_{1}-x_{0}}=\frac{1-(-1)}{2-1}=2.

(3.51)

De (3.48), temos

	$\displaystyle f(x)=m(x-x_{0})+y_{0}$		(3.52)
	$\displaystyle\text{}\quad=2(x-1)+(-1)$		(3.53)
	$\displaystyle\text{}\quad=2x-3.$		(3.54)

Ou seja, a função afim desejada é $f(x)=2x-3$ . Agora, faça o gráfico desta função para verificar o resultado!

Código 41: Python

⬇

1from sympy import Symbol, Lambda, plot

2x = Symbol('x')

3x0, y0 = 1, -1

4x1, y1 = 2, 1

5m = (y1 - y0) / (x1 - x0)

6f = Lambda(x, m*(x-x0) + y0)

7print('f(x) =', f(x))

8plot(f(x), (x, -3, 3))

f(x) = 2*x - 3

Exemplo 3.2.5.(Região entre retas)

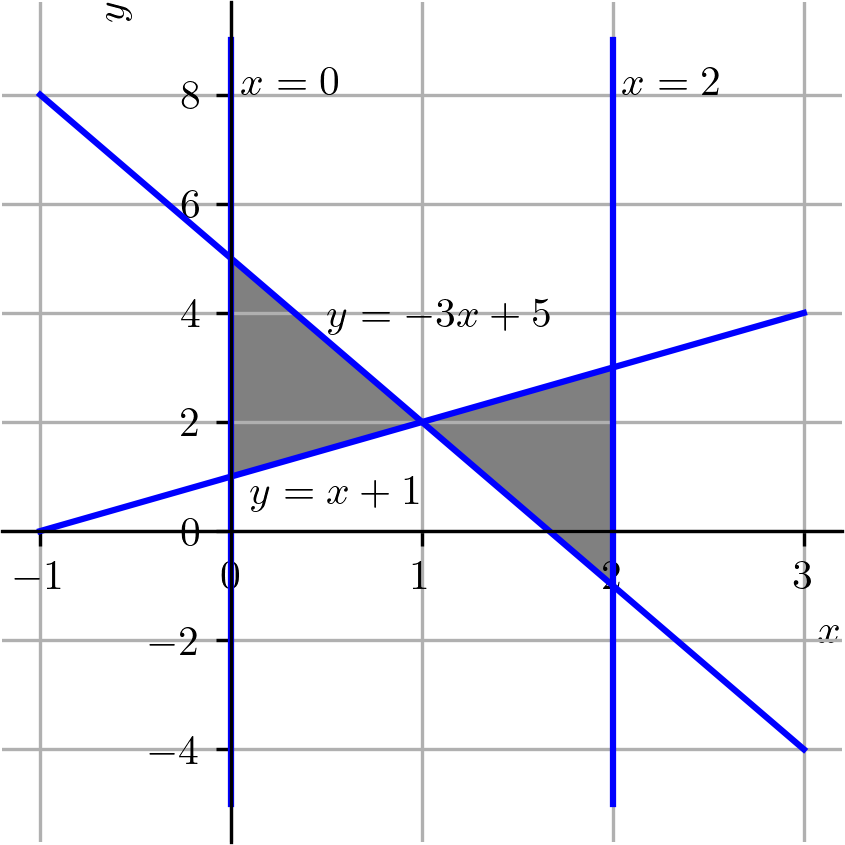
Vamos identificar (hachurar) a região do plano cartesiano delimitada pelas retas $y=x+1$ , $y=-3x+5$ , $x=0$ e $x=2$ .

A reta $y=0$ corresponde ao eixo das ordenadas e $y=2$ é a reta perpendicular ao eixo das abscissas que passa pelo ponto $(2,0)$ . Fazemos os esboços das retas em um único gráfico e então identificamos a região que está simultaneamente entre todas as retas dadas. Obtemos, assim, o gráfico da região delimitada pelas retas, consultemos a Figura 3.11.

3.2.2 Estudo de sinal

O estudo de sinal de uma função consiste em determinar as regiões de seu domínio em que seus valores de saída são negativos, zero ou positivos. Para funções afins (não constantes), o estudo de sinal é feito a partir do zero da função e do coeficiente angular. O zero de uma função $f(x)=mx+b$ é o valor de $x$ tal que $f(x)=0$ (valor de $x$ em que a reta cruza o eixo $x$ ), i.e.

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}mx+b=0.

(3.55)

Resolvendo para $x$ , temos

	$\displaystyle mx=-b$		(3.56)
	$\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% x=-\frac{b}{m}.$		(3.57)

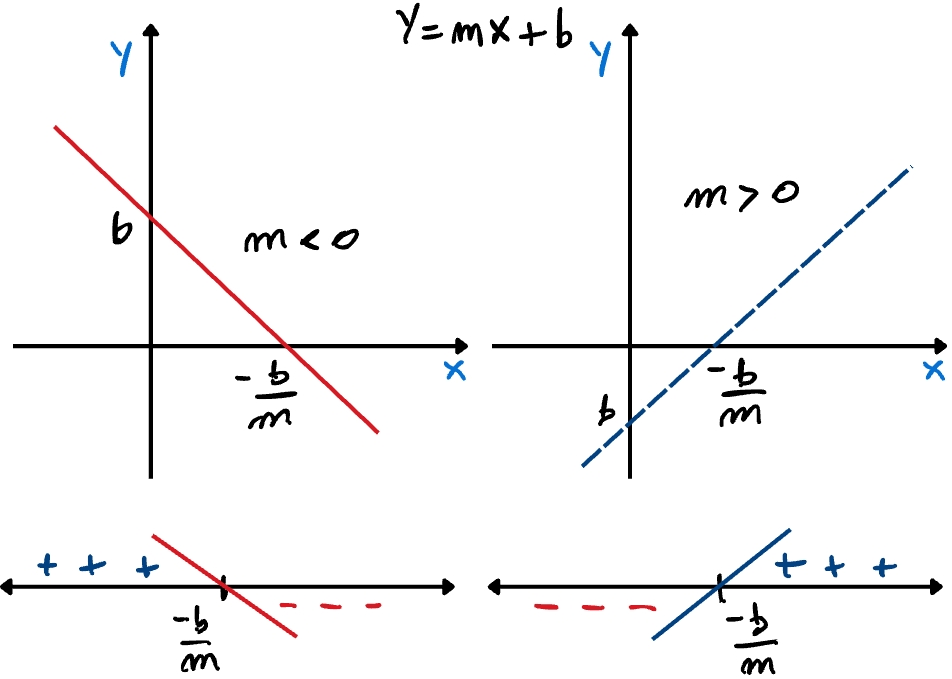
Como vimos até aqui, o coeficiente angular $m$ controla a inclinação da reta. Consultemos a Figura 3.12, temos que

•

se $m>0$ , a reta é crescente e, portanto, a função é positiva para $x$ maior que seu zero e negativa para $x$ menor que seu zero;
•

se $m<0$ , a reta é decrescente e, portanto, a função é negativa para $x$ maior que seu zero e positiva para $x$ menor que seu zero;
•

se $m=0$ , a função é constante e, portanto, é positiva ou negativa em toda parte, dependendo do valor de $b$ .

Exemplo 3.2.6.

Façamos o estudo de sinal da função

f(x)=2x+1

(3.58)

Lembramos que uma função afim com coeficiente angular positivo é crescente em toda parte. Ainda, temos que ela corta o eixo das abscissas em seu zero, i.e.

	$\displaystyle 2x+1=0$		(3.59)
	$\displaystyle 2x=-1$		(3.60)
	$\displaystyle x=-\frac{1}{2}$		(3.61)

Por tanto, concluímos que

	$x<-\frac{1}{2}$	$x=-\frac{1}{2}$	$x>-\frac{1}{2}$
$f(x)$	-	0	+

Ou seja, $f(x)$ é negativo para $x\in(-\infty,-\frac{1}{2})$ , $f(x)=0$ para $x=-\frac{1}{2}$ e $f(x)$ é positivo para $x\in(-\frac{1}{2},\infty)$ . Faça o esboço do gráfico de $f$ para verificar o resultado!

3.2.3 Exercícios

E. 3.2.1.

Determine o domínio e a imagem de cada uma das seguintes funções afins:

a)

$f(x)=-100x+1$
b)

$y=-\pi$
c)

$h(v)=2+x$

a) $D=\mathbb{R}$ ; $I=\mathbb{R}$ ; b) $D=\mathbb{R}$ , $I=\{\pi\}$ ; c) $D=\mathbb{R}$ ; $I=\mathbb{R}$

E. 3.2.2.

Faça um esboço do gráfico de cada uma das seguintes funções:

a)

$f_{1}(x)=x$
b)

$f_{2}(x)=-x$
c)

$f_{3}(x)=x-1$
d)

$f_{4}(x)=-x+1$

E. 3.2.3.

Determine a função afim $f(x)=mx+b$ , cujo gráfico contém os pontos $(-2,1)$ e $(0,-2)$ .

$f(x)=-\frac{3}{2}x-2$

E. 3.2.4.

Faça o estudo de sinal das seguintes funções:

a)

$f(x)=-2x-2$
b)

$f(x)=-2$
c)

$f(x)=2x-2$

a)

$x<-1$ $x=-1$ $x>-1$

$f(x)$ + 0 -
b)

$f(x)<0$ em toda parte
c)

$x<1$ $x=1$ $x>1$

$f(x)$ - 0 +

	$x<-1$	$x=-1$	$x>-1$
$f(x)$	+	0	-

	$x<1$	$x=1$	$x>1$
$f(x)$	-	0	+

E. 3.2.5.

Verifique se as retas $y=-x-1$ e $y=2x-3$ se interceptam e, caso afirmativo, determine o ponto de interseção.

$(2/3,-5/3)$

E. 3.2.6.

Determine o ponto de interseção dos gráficos das funções afins $f(x)=2x+1$ e $g(x)=2x-1$ .

não há

E. 3.2.7.

Faça o esboço e hachure a região do plano cartesiano que fica delimitada pelas retas $y=0$ , $y=2x+2$ e $x=1$ .

E. 3.2.8.

Na mecânica clássica, a energia cinética $E_{c}$ de um objeto não rotativo de massa $m$ [kg] movimentando-se com uma velocidade $v$ [ $\text{m}/\text{s}$ ] é dada por

E_{c}=\frac{m}{2}v^{2}

(3.62)

Assumindo $v>0$ constante, temos que $E_{c}$ é função apenas de $m$ , i.e. $E_{c}=E_{c}(m)$ . Responda cada um dos seguintes itens:

a)

Qual a classe da função $E_{c}=E_{c}(m)$ ?
b)

Qual o domínio da função $E_{c}=E_{c}(m)$ .
c)

Qual a imagem da função $E_{c}=E_{c}(m)$ .
d)

$E_{c}=E_{c}(m)$ é uma função crescente ou decresce?
e)

Se $E_{c}(1)=50$ , qual a velocidade do objeto?

a) Função linear. b) $D(E_{c})=\{m\in\mathbb{R}:\leavevmode\nobreak\ m\geq 0\}$ . c) $Im(E_{c})=\{e\in\mathbb{R}:e\geq 0\}$ . d) Crescente. e) $v=10$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados