Pré-Cálculo

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

3.1 Definição e gráfico de funções

3.1.1 Definição

Uma função de um conjunto $D$ em um conjunto $Y$ é uma regra que associa um único elemento $y\in Y$ a cada dado elemento $x\in D$ . Costumeiramente, identificamos uma função por uma letra, por exemplo, $f$ e escrevemos

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}f:D\mapsto Y,y% =f(x)

(3.1)

para denotar que a função recebe valor de entrada em $D$ e fornece valor de saída em $Y$ , seguindo uma regra de associação preestabelecida $y=f(x)$ . Usualmente, $D$ é chamado é conjunto de entrada e $Y$ de conjunto de saída.

Código 38: Python

⬇

1from sympy import Symbol, Function

2x = Symbol('x', real=True)

3f = Function('f', real=True)

4y = f(x)

5print('y in R?', y.is_real)

y in R? True

Exemplo 3.1.1.

Consultemos os seguintes exemplos:

a)

$f:\mathbb{R}\mapsto\mathbb{R}$ , $y=2x-1$

A função $f$ toma valor de entrada $x$ no conjunto dos números reais $D=\mathbb{R}$ e fornece o valor de saída $y=2x-1$ , também no conjunto dos números reais $Y=\mathbb{R}$ . A regra de associação é $y=2x-1$ . Seguem alguns exemplos de aplicação:

$\displaystyle f(x)=2x-1$ (3.2)

$\displaystyle f(-1)=2(-1)-1=-3$ (3.3)

$\displaystyle f(\sqrt{2})=2\sqrt{2}-1$ (3.4)

$\displaystyle f(z)=2z-1,\quad\forall z\in\mathbb{R}$ (3.5)

Código 39: Python

⬇

1from sympy import Symbol, Lambda, sqrt

2x = Symbol('x', real=True)

3f = Lambda(x, 2*x - 1)

4print('f(-1) =', f(-1))

5print('f(sqrt(2)) =', f(sqrt(2)))

6z = Symbol('z', real=True)

7print('f(z) =', f(z))

⬇

f(-1) = -3

f(sqrt(2)) = -1 + 2*sqrt(2)

f(z) = 2*z - 1
b)

$g:\mathbb{Z}\mapsto\mathbb{Q}$ , $\displaystyle y=\frac{1}{x}$

A função $g$ toma um valor de entrada em $D=\mathbb{Z}$ e fornece o valor de saída $\displaystyle y=\frac{1}{x}$ no conjunto dos números racionais $\mathbb{Q}$ . A regra de associação é $\displaystyle y=\frac{1}{x}$ . Segue alguns exemplos de aplicação:

$\displaystyle g(2)=\frac{1}{2}$ (3.6)

$\displaystyle g(-5)=\frac{1}{-5}=-\frac{1}{5}$ (3.7)

$\displaystyle g(u)=\frac{1}{u},\quad\forall u\in\mathbb{Z}^{*}$ (3.8)

Código 40: Python

⬇

1from sympy import symbols, Lambda, S

2x, u = symbols('x, u', integer=True)

3g = Lambda(x, S(1)/x)

4print('g(x) =', g(x))

5print('g(2) =', g(2))

6print('g(-1/5) =', g(S(-1)/5))

7print('g(u) =', g(u))

⬇

g(x) = 1/x

g(2) = 1/2

g(-1/5) = -5

g(u) = 1/u

Observação 3.1.1.(Funções reais de variável real)

Ao longo do texto, vamos assumir que as funções são definidas de $\mathbb{R}\mapsto\mathbb{R}$ , salvo explicitamente escrito diferente. Assim sendo, vamos passar a usar a notação simplificada

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}f:x\mapsto f(x).

(3.9)

Mais ainda, as funções serão descritas diretamente de suas regras associação.

3.1.2 Domínio e imagem

O conjunto $D$ de todos os possíveis valores de entrada da função é chamado de domínio. Para $f:D\mapsto Y$ , denotamos

\displaystyle\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}D_{f}:=\{x\in D% :\leavevmode\nobreak\ f(x)\in Y\},

(3.10)

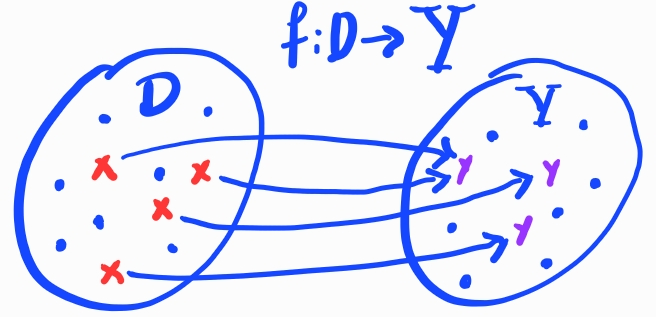
i.e. o domínio de $f$ é o conjunto de todos os valores $x\in D$ , tal que $f(x)\in Y$ . Na a Figura 3.1, temos que o domínio de $f$ é formado apenas pelos pontos marcados com x.

Figura 3.1: Domínio (pontos marcados com x) e imagem (pontos marcados com y) de uma função.

Exemplo 3.1.2.

Estudemos os seguintes casos.

a)

$f:x\mapsto f(x),y=x^{2}$

Observamos que, dado qualquer valor de entrada $x\in\mathbb{R}$ , $x^{2}$ está definido e é, também, um número real. Desta forma, a função $f$ está definida para todo $x\in\mathbb{R}$ , i.e.

$\displaystyle D_{f}=\mathbb{R}.$ (3.11)

Neste caso, dizemos que $f$ está definida em toda parte.
b)

$\displaystyle g:x\mapsto g(x),y=\frac{1}{x}$ :

Lembramos que a divisão por zero não está definida. A expressão $1/x$ está definida para todo número real não nulo, i.e. $x\in\mathbb{R}\setminus\{0\}$ . Logo, o domínio de $g$ é

$D_{g}=\mathbb{R}\setminus\{0\}.$ (3.12)

Equivalentemente, escrevemos que $g$ está definida para todo $x\in(-\infty,0)\cup(0,\infty)$ , ou ainda, simplesmente para todo $x\neq 0$ .
c)

$y=\sqrt{1-x^{2}}$

A partir da regra, entendemos que $y$ é função de $x$ , i.e. $y\mapsto y(x)$ . Aqui, observamos que a raiz quadrada está definida apenas para números reais não negativos. Logo, esta função está definida para $x$ tal que

$\displaystyle 1-x^{2}\geq 0$ (3.13)

$\displaystyle-x^{2}\geq-1$ (3.14)

$\displaystyle x^{2}\leq 1$ (3.15)

$\displaystyle\sqrt{x^{2}}\leq\sqrt{1}$ (3.16)

$\displaystyle|x|\leq 1$ (3.17)

$\displaystyle-1\leq x\leq 1$ (3.18)

Concluímos que seu domínio é $x\in[-1,1]$ .

Dada uma função $f:D\mapsto Y$ , o conjunto de todos os valores $f(x)\in Y$ tal que $x\in D$ é chamado de imagem da função. Em notação de conjunto, temos

I_{f}=\{y\in Y:y=f(x)\land x\in D\},

(3.19)

i.e. o conjunto de todos os valores $y\in Y$ tal que $y=f(x)$ e $x\in D$ . Na Figura 3.1, temos que a imagem de $f$ é formada pelos pontos marcados com y.

Exemplo 3.1.3.

Estudemos os seguintes casos.

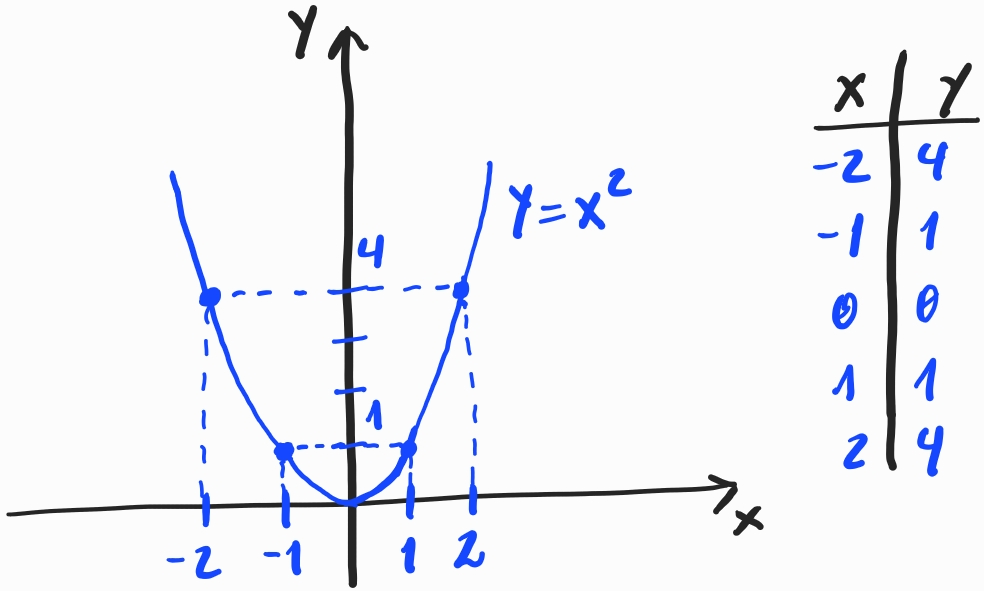
a)

$f:\mathbb{R}\to\mathbb{R},y=x^{2}$ :

Observamos que para qualquer número real $x$ , temos $y=x^{2}\geq 0$ . Além disso, para cada número real não negativo $y$ , temos que

$\displaystyle x^{2}=y$ (3.20)

$\displaystyle|x|=\sqrt{y}$ (3.21)

$\displaystyle x=\sqrt{y}\text{ ou }x=-\sqrt{y}.$ (3.22)

Logo, concluímos que a imagem de $f$ é

$I_{f}=\mathbb{R}_{+}=[0,\infty).$ (3.23)

i.e. o conjunto de todos os $y\geq 0$ .
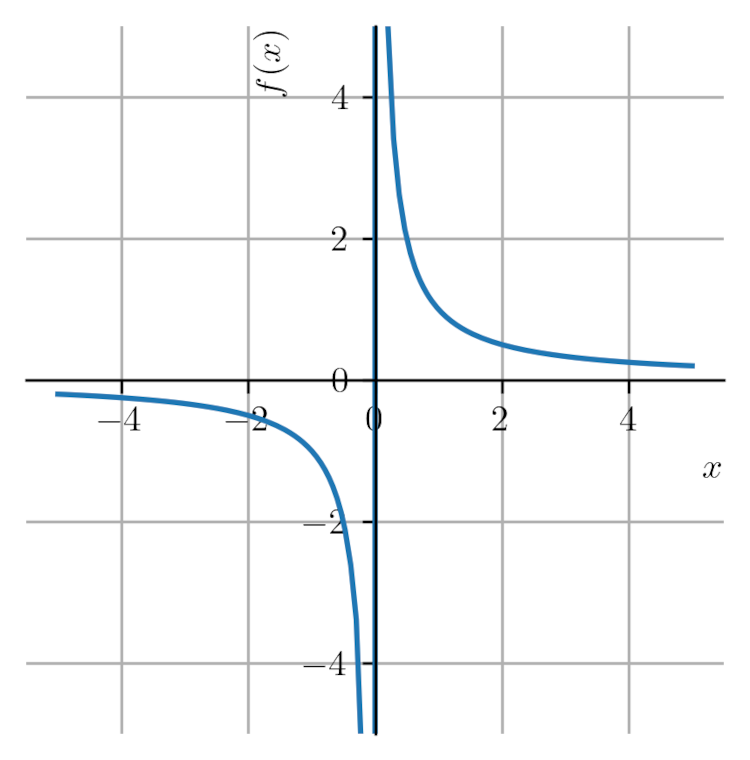
b)

$y=1/x$ :

Primeiramente, observemos que se $y=0$ , então não existe número real tal que $0=1/x$ . Ou seja, $0$ não pertence a imagem desta função. Por outro lado, dado qualquer número $y\neq 0$ , temos que

$\displaystyle\frac{1}{x}=y$ (3.24)

$\displaystyle x=\frac{1}{y}.$ (3.25)

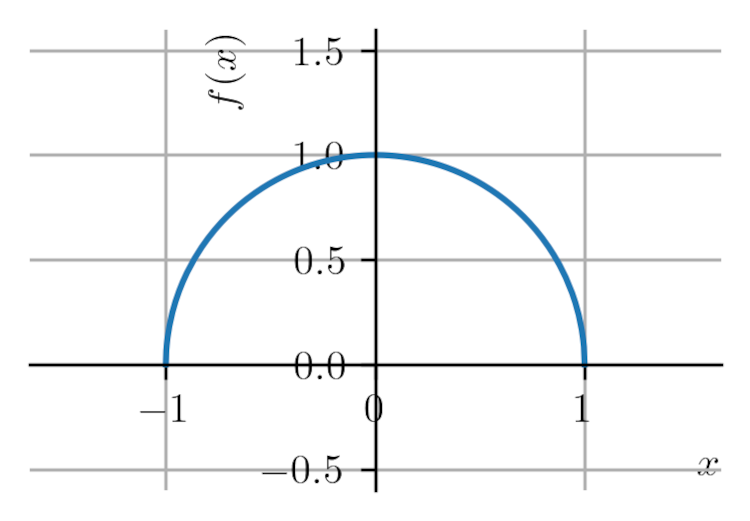
Logo, concluímos que a imagem desta função é o conjunto de todos os números reais não nulos, i.e. $\mathbb{R}^{*}=(-\infty,0)\cup(0,\infty)$ .
c)

$y=\sqrt{1-x^{2}}$ :

No Exemplo 3.1.2, vimos que esta função está definida apenas para $-1\leq x\leq 1$ . Ainda, $y\geq 0$ e, para $x$ restrito a este intervalo, temos que

$\displaystyle y=\sqrt{1-x^{2}}$ (3.26)

$\displaystyle y^{2}=1-x^{2}$ (3.27)

$\displaystyle x^{2}=1-y^{2}$ (3.28)

$\displaystyle 0\leq 1-y^{2}\leq 1$ (3.29)

$\displaystyle 0\leq y^{2}\leq 1$ (3.30)

$\displaystyle 0\leq y\leq 1$ (3.31)

Ou seja, a imagem desta função é o intervalo $[0,1]$ .

Observação 3.1.2.(Domínio e imagem em aplicações)

Em aplicações, o domínio e imagem de funções também podem ficar restritos à modelagem do problema. Por exemplo, pela lei geral dos gases, o produto da pressão $P$ pelo volume $V$ de uma gás é função da temperatura $T$ como segue

P=\frac{K}{V_{0}}\cdot T,

(3.33)

onde $V_{0}$ é o volume dado do gás e $K>0$ é uma constante que depende do gás. A temperatura é dada em Kelvin¹¹1William Thomson, 1º Barão Kelvin, 1824 - 1907, físico e engenheiro britânico. Fonte: Wikipédia: Lorde Kelvin., logo $T\geq 0$ . Entendendo a pressão $P$ como função de $T$ , temos que o domínio é $T_{0}<T<T_{1}$ , onde $T_{0}$ é a menor temperatura que o gás admite e $T_{1}$ é a maior temperatura que o gás admite. A imagem é, então, $\frac{K}{V_{0}}T_{0}<P<\frac{K}{V_{0}}T_{1}$ .

3.1.3 Gráfico

O gráfico de uma função $f$ é o conjunto dos pontos (ou pares ordenados) $(x,f(x))$ tal que $x$ pertence ao domínio da função. Mais precisamente, para uma função $f:D\to Y\mathbb{R}$ , o gráfico é o conjunto

\color[rgb]{0,0,1}\definecolor[named]{pgfstrokecolor}{rgb}{0,0,1}% \pgfsys@color@rgb@stroke{0}{0}{1}\pgfsys@color@rgb@fill{0}{0}{1}G_{f}=\{(x,f(x% ))\in\mathbb{D}\times\mathbb{Y}:\leavevmode\nobreak\ x\in D_{f}\}.

(3.34)

O esboço do gráfico de uma função é, costumeiramente, uma representação geométrica dos pontos de seu gráfico em um plano cartesiano $x-y$ .

Exemplo 3.1.4.

Na sequência, temos os esboços dos gráficos de funções selecionadas.

a)

$f(x)=x^{2}$

Figura 3.2: Esboço do gráfico de $f(x)=x^{2}$ .

Código 41: Python

⬇

1from sympy import Symbol, plot

2x = Symbol('x')

3plot(x**2, (x, -3, 3))
b)

$\displaystyle y=\frac{1}{x}$

Figura 3.3: Esboço do gráfico de $\displaystyle y=\frac{1}{x}$ .

Código 42: Python

⬇

1from sympy.plotting import plot

2from sympy.abc import x

3plot(1/x, (x, -5, 5), ylim=[-5, 5])
c)

$y=\sqrt{1-x^{2}}$

Figura 3.4: Esboço do gráfico de $y=\sqrt{1-x^{2}}$ .

3.1.4 Categorias de funções

Funções algébricas

Funções algébricas são funções definidas a partir de somas, subtrações, multiplicações, divisões ou extração de raízes de funções polinomiais. Funções polinomiais e as funções algébricas derivadas são estudas nas próximas seções.

Exemplo 3.1.5.

São exemplos de funções algébricas:

a)

$\displaystyle f(x)=2$
b)

$\displaystyle g(x)=2x-1$
c)

$\displaystyle h(x)=2-x^{3}+x$
d)

$\displaystyle f_{1}(u)=\frac{u^{2}+2u+1}{u-1}$
e)

$\displaystyle y=2^{z}-\sqrt{z-1}$

Funções transcendentes

Funções transcendentes são funções que não são algébricas. Como exemplos, temos as funções trigonométricas, exponencial e logarítmica, as quais são introduzidas nas próximas seções.

Exemplo 3.1.6.

São exemplos de funções transcendentes:

a)

$\displaystyle f(x)=e^{-x^{2}}$
b)

$\displaystyle y=\log_{2}(2x-1)$
c)

$\displaystyle g(v)=\operatorname{sen}(v)-\cos(v)$
d)

$\displaystyle h(u)=\operatorname{arctg}(u)$

Funções definidas por partes

Funções definidas por partes são funções definidas por diferentes expressões matemáticas em diferentes partes de seu domínio.

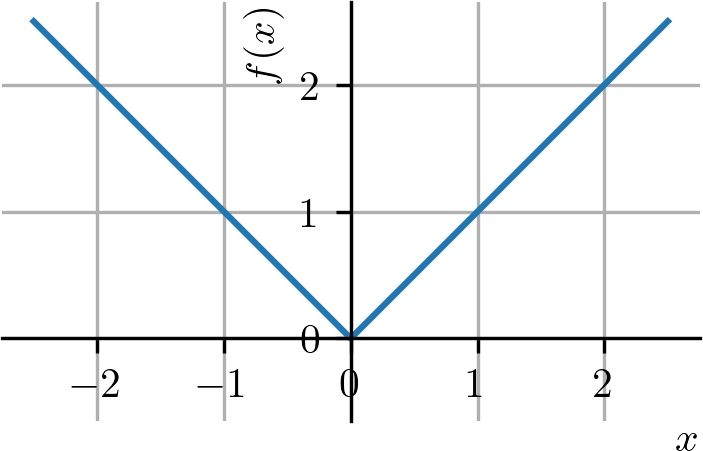
Um exemplo fundamental de função definida por partes é a função valor absoluto

|x|=\left\{\begin{array}[]{ll}x&,x\geq 0\\ -x&,x<0\end{array}\right.

(3.35)

Consultemos seu gráfico na Figura 3.5.

Figura 3.5: Esboço do gráfico da função valor absoluto $y=|x|$ .

Código 43: Python

⬇

1from sympy import Abs

2Abs(-1)

3.1.5 Exercícios

E. 3.1.1.

Determine o domínio e a imagem da função identidade, i.e. $f(x)=x$ . Então, faça o esboço de seu gráfico.

Domínio: $\mathbb{R}$ ; Imagem: $\mathbb{R}$

E. 3.1.2.

Determine o domínio e a imagem da função $f(x)=x^{2}+1$ . Então, faça o esboço de seu gráfico.

Domínio: $\mathbb{R}$ ; Imagem: $[1,\infty)$ .

E. 3.1.3.

Determine o domínio e a imagem da função $f(x)=1-x^{2}$ . Então, faça o esboço de seu gráfico.

Domínio: $\mathbb{R}$ ; Imagem: $(-\infty,1]$ .

E. 3.1.4.

Determine o domínio e a imagem da função

h(x)=\frac{1}{x-1}-2.

(3.36)

Então, faça o esboço de seu gráfico.

Domínio: $(-\infty,1)\cup(1,\infty)$ ; Imagem: $(-\infty,-2)\cup(-2,\infty)$ .

E. 3.1.5.

Determine o domínio e a imagem da função valor absoluto.

Domínio: $\mathbb{R}$ ; Imagem: $[0,\infty)$ .

Envie seu comentário

Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

Este texto é disponibilizado nos termos da Licença Creative Commons Atribuição-CompartilhaIgual 4.0 Internacional. Ícones e elementos gráficos podem estar sujeitos a condições adicionais.

Política de uso de dados