Colabore! Saiba mais screen_rotation

Ao navegar por este site , você concorda com a Política de Uso de Dados.

| | | | |

1 Problemas Unidimensionais 1.1 Interpolação e Projeção 1.3 Condições de Contorno

1.2 Problema Modelo

Ajude a manter o site livre, gratuito e sem propagandas. Colabore!

Em revisão

Nesta seção, discutimos sobre a aplicação do método de elementos finitos para o seguinte problema de valor de contorno: encontrar $u$ tal que

	$\displaystyle-u^{\prime\prime}$	$\displaystyle=f,\quad x\in I=[0,L],$		(1.59)
	$\displaystyle u(0)$	$\displaystyle=u(L)=0,$		(1.60)

onde $f$ é uma função dada.

1.2.1 Formulação Fraca

Em revisão

A derivação de um método de elementos finitos inicia-se da formulação fraca do problema em um espaço de funções apropriado. No caso do problema (1.59)-(1.60), tomamos o espaço

V_{0}=\{v\in H^{1}(I):\leavevmode\nobreak\ v(0)=v(1)=0\}.

(1.61)

Ou seja, se $v\in H^{1}(I)$ , então $\|v\|_{L^{2}(I)}<\infty$ , $\|v^{\prime}\|_{L^{2}(I)}<\infty$ , bem como $v$ satisfaz as condições de contorno do problema.

A formulação fraca é, então, obtida multiplicando-se a equação (1.59) por uma função teste $v\in V_{0}$ (arbitrária) e integrando-se por partes, i.e.

	$\displaystyle\int_{I}fv\,dx$	$\displaystyle=-\int_{I}u^{\prime\prime}v\,dx$		(1.62)
		$\displaystyle=\int_{I}u^{\prime}v^{\prime}\,dx-u^{\prime}(L)v(L)+u^{\prime}(0)% v(0)$		(1.63)

Donde, das condições de contorno, temos

\int_{I}u^{\prime}v^{\prime}\,dx=\int_{I}fv\,dx.

(1.65)

Desta forma, o problema fraco associado a (1.59)-(1.60) lê-se: encontrar $u\in V_{0}$ tal que

a(u,v)=L(v),\quad\forall v\in V_{0},

(1.66)

onde

	$\displaystyle a(u,v)$	$\displaystyle=\int_{I}u^{\prime}v^{\prime}\,dx$		(1.67)
	$\displaystyle L(v)$	$\displaystyle=\int_{I}fv\,dx,$		(1.68)

são chamadas de forma bilinear e forma linear, respectivamente.

1.2.2 Formulação de Elementos Finitos

Em revisão

Uma formulação de elementos finitos é um aproximação do problema fraco (1.66) em um espaço de dimensão finita. Aqui, vamos usar o espaço $V_{h,0}$ das funções lineares por partes em $I$ que satisfazem as condições de contorno, i.e.

V_{h,0}=\{v\in V_{h}:\leavevmode\nobreak\ v(0)=v(L)=0\}.

(1.69)

Então, substituindo o espaço $V_{0}$ pelo subespaço $V_{h,0}\subset V_{0}$ em (1.66), obtemos o seguinte problema de elementos finitos: encontrar $u_{h}\in V_{h,0}$ tal que

a(u_{h},v)=L(v),\quad\forall v\in V_{h,0}.

(1.70)

Observação 1.2.1.

A formulação de elementos finitos não é única, podendo-se trabalhar com outros espaços de funções. No caso em que o espaço da solução é igual ao espaço das funções testes, a abordagem é chamada de método de Galerkin⁴⁴endnote: ⁴Boris Grigoryevich Galerkin, matemático e engenheiro soviético. Fonte: Wikipédia..

Observemos que o problema (1.70) é equivalente a: encontrar $u_{h}\in V_{h,0}$ tal que

a(u_{h},\varphi_{i})=L(\varphi_{i}),\quad i=1,\dotsc,n-1,

(1.71)

onde $\varphi_{i}$ , $i=1,\dotsc,n-1$ , são as funções base de $V_{h,0}$ . Então, como $u_{h}\in V_{h,0}$ , temos

u_{h}=\sum_{j=1}^{n-1}\xi_{j}\varphi_{j},

(1.72)

onde $\xi_{j}$ , $j=1,2,\dotsc,n-1$ , são incógnitas a determinar. I.e., ao computarmos $\xi_{j}$ , $j=1,2,\dotsc,n-1$ , temos obtido a solução $u_{h}$ do problema de elementos finitos 1.70.

Agora, da forma bilinear (1.67), temos

	$\displaystyle a(u_{h},\varphi_{i})$	$\displaystyle=a\left(\sum_{j=1}^{n-1}\xi_{j}\varphi_{j},\varphi_{i}\right)$		(1.73)
		$\displaystyle=\sum_{j=1}^{n-1}\xi_{j}a(\varphi_{j},\varphi_{i}).$		(1.74)

Daí, o problema (1.70) é equivalente a resolvermos o seguinte sistema de equações lineares

A\xi=b,

(1.75)

onde $A=[a_{i,j}]_{i,j=1}^{n-1}$ é a matriz de rigidez com

a_{i,j}=a(\varphi_{j},\varphi_{i})=\int_{I}\varphi_{j}^{\prime}\varphi_{i}^{% \prime}\,dx,

(1.76)

$\xi=(\xi_{1},\xi_{2},\dotsc,\xi_{n-1})$ é o vetor das incógnitas e $b=(b_{i})_{i=1}^{n-1}$ é o vetor de carregamento com

b_{i}=L(\varphi_{i})=\int_{I}f\varphi_{i}\,dx.

(1.77)

Exemplo 1.2.1.

Consideramos o problema (1.59)-(1.60) com $f\equiv 1$ e $L=1$ , i.e.

	$\displaystyle-u^{\prime\prime}$	$\displaystyle=1,\quad x\in I=[0,1],$		(1.78)
	$\displaystyle u(0)$	$\displaystyle=u(1)=0.$		(1.79)

Neste caso, a solução analítica $u(x)=-x^{2}/2+x/2$ pode ser facilmente obtida por integração.

Agora, vamos computar uma aproximação de elementos finitos no espaço das funções lineares por partes $V_{h,0}=\{v\in P_{1}(I);\leavevmode\nobreak\ v(0)=v(1)=0\}$ construído numa malha uniforme de $5$ células no intervalo $I=[0,1]$ . Para tanto, consideramos o problema fraco: encontrar $u\in V_{0}=\{v\in H^{1}(I);\leavevmode\nobreak\ v(0)=v(L)=0\}$ tal que

a(u,v)=L(v),

(1.80)

onde

a(u,v)=\int_{I}u^{\prime}v^{\prime}\,dx,\quad L(v)=\int_{I}fv\,dx.

(1.81)

Então, a formulação de elementos finitos associada, lê-se: encontrar $u_{h}\in V_{h,0}$ tal que

a(u_{h},v_{h})=L(v_{h}),\quad\forall v_{h}\in V_{h,0}.

(1.82)

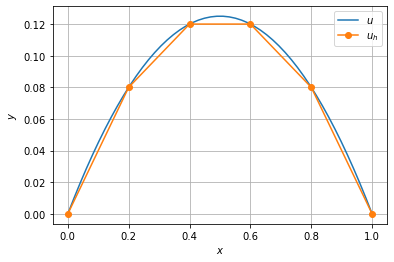
A Figura LABEL:fig:ex_modelo apresenta o esboço dos gráficos da solução analítica $u$ e da sua aproximação de elementos finitos $u_{h}$ .

Refer to caption — Figura 1.5: Esboço dos gráficos das soluções referentes ao Exemplo 1.2.1.

Código 3: ex_mef1d_modelo.py

⬇

1from mpi4py import MPI

3# malha

4from dolfinx import mesh

5domain = mesh.create_unit_interval(MPI.COMM_WORLD,

6 nx = 5)

7# espaço

8from dolfinx import fem

9V = fem.functionspace(domain, ('P', 1))

11# condição de contorno

12import numpy as np

13uD = fem.Function(V)

14uD.interpolate(lambda x: np.full(x.shape[1], 0.))

16tdim = domain.topology.dim

17fdim = tdim - 1

18domain.topology.create_connectivity(fdim, tdim)

19boundary_facets = mesh.exterior_facet_indices(domain.topology)

20boundary_dofs = fem.locate_dofs_topological(V, fdim,

21 boundary_facets)

22bc = fem.dirichletbc(uD, boundary_dofs)

24# problema mef

25import ufl

26from dolfinx import default_scalar_type

27from dolfinx.fem.petsc import LinearProblem

28u = ufl.TrialFunction(V)

29v = ufl.TestFunction(V)

31f = fem.Constant(domain, default_scalar_type(1.))

33a = ufl.dot(ufl.grad(u), ufl.grad(v)) * ufl.dx

34L = f * v * ufl.dx

36problem = LinearProblem(a, L, bcs=[bc])

37uh = problem.solve()

1.2.3 Estimativa a Priori

Em revisão

Existem dois tipos de estimativas do erro $e:=u-u_{h}$ . Estimativas a priori, são aquelas em que o erro é dado em relação da solução $u$ , enquanto que nas estimativas a posteriori o erro é expresso em relação a solução de elementos finitos $u_{h}$ .

Teorema 1.2.1.

(Ortogonalidade de Galerkin.) A solução de elementos finitos $u_{h}$ de (1.70) satisfaz a seguinte propriedade de ortogonalidade

a(u-u_{h},v):=\int_{I}(u-u_{h})^{\prime}v^{\prime}\,dx=0,\quad v\in V_{h,0},

(1.83)

onde $u$ é a solução de (1.66).

Demonstração.

De (1.70), (1.66) e lembrando que $V_{h,0}\subset V_{0}$ , temos

a(u,v)=L(v)=a(u_{h},v)\Rightarrow a(u-u_{h},v)=0,

(1.84)

para todo $v\in V_{h,0}$ . ∎

Teorema 1.2.2.

(A melhor aproximação.) A solução de elementos finitos $u_{h}$ dada por (1.70) satisfaz a seguinte propriedade de melhor aproximação

\|(u-u_{h})^{\prime}\|_{L^{2}(I)}\leq\|(u-v)^{\prime}\|_{L^{2}(I)},\quad v\in V% _{h,0},

(1.85)

onde $u$ é a solução de (1.66).

Demonstração.

Escrevendo $u-u_{h}=u-v+v-u_{h}$ para qualquer $v\in V_{h,0}$ e usando a ortogonalidade de Galerkin (Teorema 1.2.1), temos

$\displaystyle\\|(u-u_{h})^{\prime}\\|_{L^{2}(I)}^{2}$	$\displaystyle=\int_{I}(u-u_{h})^{\prime}(u-u_{h})^{\prime}\,dx$	(1.86)
	$\displaystyle=\int_{I}(u-u_{h})^{\prime}(u-v+v-u_{h})^{\prime}\,dx$	(1.87)
	$\displaystyle=\int_{I}(u-u_{h})^{\prime}(u-v)^{\prime}\,dx+\int_{I}(u-u_{h})^{% \prime}(v-u_{h})^{\prime}\,dx$	(1.88)
	$\displaystyle=\int_{I}(u-u_{h})^{\prime}(u-v)^{\prime}\,dx$	(1.89)
	$\displaystyle\leq\\|(u-u_{h})^{\prime}\\|_{L^{2}(I)}\\|(u-v)^{\prime}\\|_{L^{2}(I)}.$	(1.90)

∎

Teorema 1.2.3.

(Estimativa a priori.) O erro em se aproximar a solução $u$ de (1.66) pela solução de elementos finitos $u_{h}$ dada por (1.70) satisfaz a seguinte estimativa a priori

\|(u-u_{h})^{\prime}\|_{L^{2}(I)}^{2}\leq C\sum_{i=1}^{n}h_{i}^{2}\|u^{\prime% \prime}\|_{L^{2}(I_{i})}^{2}.

(1.91)

Demonstração.

Tomando $v=\pi u$ no teorema da melhor aproximação (Teorema 1.2.2), obtemos

\|(u-u_{h})^{\prime}\|_{L^{2}(I)}\leq\|(u-\pi u)^{\prime}\|_{L^{2}(I)}.

(1.92)

Daí, da estimativa do erro de interpolação (Proposição 1.1.2), temos

\|(u-u_{h})^{\prime}\|_{L^{2}(I)}^{2}\leq C\sum_{i=1}^{n}h_{i}^{2}\|u^{\prime% \prime}\|_{L^{2}(I_{i})}^{2}.

(1.93)

∎

Exemplo 1.2.2.

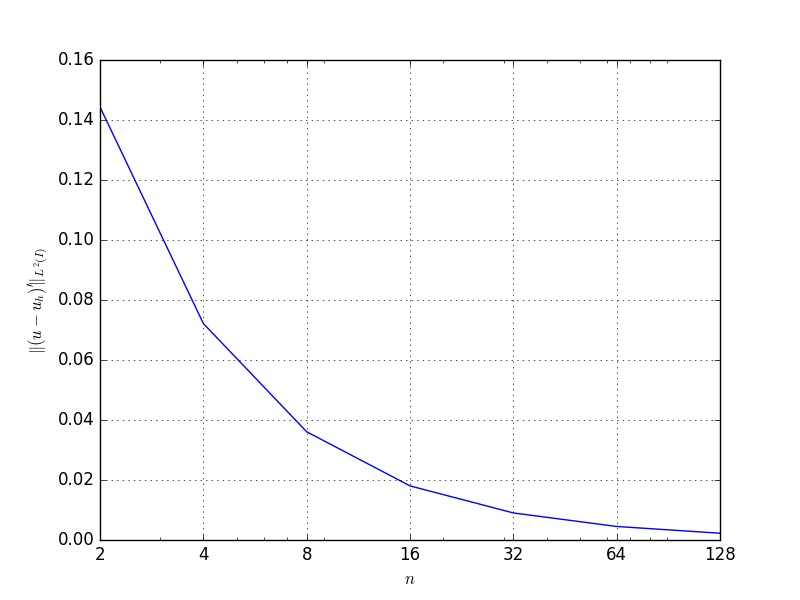
A Figura 1.6 apresenta o esboço da evolução do erro $\|(u-u_{h})^{\prime}\|_{L^{2}(I)}$ da solução de elementos finitos do problema (1.78)-(1.79) para malhas uniformes com $n=2,4,8,\ldots,128$ células.

Com o FEniCS, a computação do problema de elementos finitos pode ser feita com o seguinte código:

from __future__ import print_function, division
from fenics import *
import numpy as np
import matplotlib.pyplot as plt

def boundary(x,on_boundary):
    return on_boundary

def solver(n):
    # malha
    mesh = IntervalMesh(n,0,1)

    # espaco
    V = FunctionSpace(mesh, ’P’, 1)

    bc = DirichletBC(V,Constant(0.0),boundary)

    #MEF problem
    u = TrialFunction(V)
    v = TestFunction(V)
    f = Constant(1.0)
    a = u.dx(0)*v.dx(0)*dx
    L = f*v*dx

    #computa a sol
    u = Function(V)
    solve(a == L, u, bc)

    return u, mesh

#sol analitica
ua = Expression(’-x[0]*x[0]/2+x[0]/2’,
                degree=2)


lerrors=[]
for n in [2,4,8,16,32,64,128]:
    u, mesh = solver(n)
    e = errornorm(u,ua,norm_type=’H10’,mesh=mesh)
    lerrors.append(e)

plt.plot([2,4,8,16,32,64,128],lerrors)
plt.xscale(’log’,basex=2)
#plt.yscale(’log’,base=2)
plt.xlabel(r"$n$")
plt.ylabel(r"$|\!|(u-u_h)’|\!|_{L^2(I)}$")
plt.xlim((2,128))
plt.xticks([2,4,8,16,32,64,128],[2,4,8,16,32,64,128])
plt.grid(’on’)
plt.show()

1.2.4 Estimativa a Posteriori

Em revisão

Aqui, vamos obter uma estimativa a posteriori para o erro $e=u-u_{h}$ da solução de elementos finitos $u_{h}$ do problema (1.59)-(1.60).

Teorema 1.2.4.

A solução de elementos finitos $u_{h}$ satisfaz

\|(u-u_{h})^{\prime}\|_{L^{2}(I)}^{2}\leq C\sum_{i=1}^{n}\eta_{i}^{2}(u_{h}),

(1.94)

onde $\eta_{i}(u_{h})$ é chamado de elemento residual e é dado por

\eta_{i}(u_{h})=h_{i}\|f-u_{h}^{\prime\prime}\|_{L^{2}(I_{i})}.

(1.95)

Demonstração.

Tomando $e=u-u_{h}$ e usando a ortogonalidade de Galerkin (Teorema 1.2.1) temos

\|e^{\prime}\|_{L^{2}(I)}^{2}=\int_{I}e^{\prime}(e-\pi e)^{\prime}\,dx=\sum_{i% =1}^{n}\int_{I_{i}}e^{\prime}(e-\pi e)^{\prime}\,dx.

(1.96)

Então, aplicando integração por partes

\|e^{\prime}\|_{L^{2}(I)}^{2}=\sum_{i=1}^{n}\int_{I_{i}}(-e^{\prime\prime})(e-% \pi e)\,dx+[e^{\prime}(e-\pi e)]_{x_{i-1}}^{x_{i}}.

(1.97)

Daí, observando que $e-\pi e=0$ nos extremos dos intervalos $I_{i}$ e que $-e^{\prime\prime}=-(u-u_{h})^{\prime\prime}=-u^{\prime\prime}+u_{h}^{\prime% \prime}=f+u_{h}^{\prime\prime}$ , temos

\|e^{\prime}\|_{L^{2}(I)}^{2}=\sum_{i=1}^{n}\int_{I_{i}}(f+u_{h}^{\prime\prime% })(e-\pi e)\,dx.

(1.98)

Agora, usando as desigualdades de Cauchy-Schwarz e a estimativa padrão de interpolação (1.26), obtemos

$\displaystyle\\|e^{\prime}\\|_{L^{2}(I)}^{2}$	$\displaystyle\leq\sum_{i=1}^{n}\\|f+u_{h}\\|_{L^{2}(I_{i})}\\|e-\pi e\\|_{L^{2}(I_% {i})}\,dx$	(1.99)
	$\displaystyle\leq C\sum_{i=1}^{n}h_{i}\\|f+u_{h}\\|_{L^{2}(I_{i})}\\|e^{\prime}\\|% _{L^{2}(I_{i})}$	(1.100)
	$\displaystyle\leq C\left(\sum_{i=1}^{n}h_{i}^{2}\\|f+u_{h}\\|_{L^{2}(I_{i})}^{2}% \right)^{1/2}\left(\sum_{i=1}^{n}\\|e^{\prime}\\|_{L^{2}(I_{i})}^{2}\right)^{1/2}$	(1.101)
	$\displaystyle=C\left(\sum_{i=1}^{n}h_{i}^{2}\\|f+u_{h}\\|_{L^{2}(I_{i})}^{2}% \right)^{1/2}\\|e^{\prime}\\|_{L^{2}(I)},$	(1.102)

donde segue o resultado desejado. ∎

Observação 1.2.2.

No caso da solução de elementos finitos no espaço das funções lineares por partes, temos $u_{h}^{\prime\prime}=0$ . Logo, o elemento residual se resume em $\eta_{i}(u_{h})=h_{i}\|f\|_{L^{2}(I_{i})}$ .

1.2.5 Exercícios

Em revisão

E. 1.2.1.

Obtenha uma aproximação por elementos finitos lineares por partes da solução de

	$\displaystyle-u^{\prime\prime}+u=2\operatorname{sen}x,\quad\forall x\in(-\pi,% \pi),$		(1.103)
	$\displaystyle u(-\pi)=u(\pi)=0.$		(1.104)

Resposta.

Código FENiCS.

Envie seu comentário

As informações preenchidas são enviadas por e-mail para o desenvolvedor do site e tratadas de forma privada. Consulte a Política de Uso de Dados para mais informações. Aproveito para agradecer a todas/os que de forma assídua ou esporádica contribuem enviando correções, sugestões e críticas!

| | | |

$\displaystyle\\|e^{\prime}\\|_{L^{2}(I)}^{2}$	$\displaystyle\leq\sum_{i=1}^{n}\\|f+u_{h}\\|_{L^{2}(I_{i})}\\|e-\pi e\\|_{L^{2}(I_% {i})}\,dx$	(1.99)
	$\displaystyle\leq C\sum_{i=1}^{n}h_{i}\\|f+u_{h}\\|_{L^{2}(I_{i})}\\|e^{\prime}\\|% _{L^{2}(I_{i})}$	(1.100)
	$\displaystyle\leq C\left(\sum_{i=1}^{n}h_{i}^{2}\\|f+u_{h}\\|_{L^{2}(I_{i})}^{2}% \right)^{1/2}\left(\sum_{i=1}^{n}\\|e^{\prime}\\|_{L^{2}(I_{i})}^{2}\right)^{1/2}$	(1.101)
	$\displaystyle=C\left(\sum_{i=1}^{n}h_{i}^{2}\\|f+u_{h}\\|_{L^{2}(I_{i})}^{2}% \right)^{1/2}\\|e^{\prime}\\|_{L^{2}(I)},$	(1.102)